Кривая ошибок
Материал из MachineLearning.
(→Описание алгоритма) |
(Перенос абзаца в соседний раздел.) |
||
| (16 промежуточных версий не показаны.) | |||
| Строка 1: | Строка 1: | ||
| - | '''Кривая ошибок''' или '''ROC-кривая''' – | + | {{TOCright}} |
| + | '''Кривая ошибок''' или '''ROC-кривая''' – графичекая характеристика качества бинарного классификатора, зависимость доли верных положительных классификаций от доли ложных положительных классификаций при варьировании порога решающего правила. Преимуществом ROC-кривой является её инвариантность относительно отношения [[цена ошибки|цены ошибки]] I и II рода. | ||
| - | == | + | == Задача классификации == |
| + | Рассмотрим задачу [[классификация|классификации]] в случае двух классов, называемых «положительным» и «отрицательным». Обозначим множество классов через <tex>Y=\{-1,+1\}</tex>. Большинство известных [[классификатор|классификаторов]] могут быть представлены в виде | ||
| + | ::<tex>a(x) = \textrm{sign} (f(x,w) - w_0),</tex> | ||
| + | где | ||
| + | <tex>x</tex> — произвольный [[объект]], | ||
| + | <tex>f(x,w)</tex> — [[дискриминантная функция]], | ||
| + | <tex>w</tex> — вектор параметров, определяемый по [[обучающая выборка|обучающей выборке]], | ||
| + | <tex>w_0</tex> — порог. | ||
| + | Уравнение <tex>f(x,w)=w_0</tex> определяет [[разделяющая поверхность|разделяющую поверхность]]. | ||
| + | Примером является [[линейный классификатор]], в котором дискриминантная функция имеет вид скалярного произведения вектора описания объекта на вектор параметров: | ||
| + | <tex>a(x) = \textrm{sign} (\langle x,w \rangle - w_0)</tex>. | ||
| - | + | Пусть <tex>\lambda_y</tex> – цена ошибки (штраф за ошибку) на объекте класса <tex>y \in \{-1, +1\}</tex>. | |
| - | + | Для [[байесовский классификатор|байесовского классификатора]] при достаточно общих предположениях доказано, что оптимальное значение порога <tex>w_0</tex> зависит только от соотношения цены ошибок: | |
| + | :: <tex>w_0 = \ln\frac{\lambda_{-1}}{\lambda_{+1}},</tex> | ||
| + | тогда как оптимальное значение вектора параметров <tex>w</tex>, наоборот, зависит от выборки и не зависит от цены ошибок. | ||
| + | Таким образом, варьирование порога <tex>w_0</tex> для многих классификаторов эквивалентно варьированию отношения цены ошибок на отрицательных и положительных объектах. | ||
| + | На практике цены ошибок зависят от особенностей конкретной задачи (например, от различных экономических соображений или экспертных оценок) и могут многократно пересматриваться. | ||
| - | + | Заметим, что частным случаем линейного байесовского классификатора является [[логистическая регрессия]]. | |
| - | '' | + | ''ROC-кривая'' наглядно представляет, каким будет качество классификации при различных <tex>w_0</tex> и фиксированном <tex>w</tex>. |
== TPR и FPR == | == TPR и FPR == | ||
| + | Пусть задана выборка объектов <tex>X^m = (x_1,\ldots,x_m)</tex> с соответствующими им верными ответами <tex>y_1,\ldots,y_m</tex>. | ||
| + | Тогда для классификатора <tex>a(x)</tex> можно определить две характеристики качества: | ||
| + | #Доля ложных положительных классификаций (False Positive Rate, FPR): | ||
| + | #:<tex>\textrm{FPR}(a,X^m) = \frac{\sum_{i=1}^m [a(x_i) = +1][y_i = -1]}{\sum_{i=1}^m [y_i = -1]};</tex> | ||
| + | #Доля верных положительных классификаций (True Positive Rate, TPR): | ||
| + | #:<tex>\textrm{TPR}(a,X^m) = \frac{\sum_{i=1}^m [a(x_i) = +1][y_i = +1]}{\sum_{i=1}^m [y_i = +1]}.</tex> | ||
| - | + | == ROC-кривая == | |
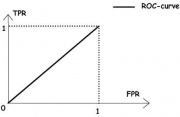
| + | [[Изображение:RoC-1.jpg|thumb|Рис.1. «Случайное гадание».]] | ||
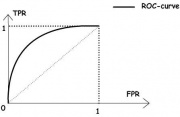
| + | [[Изображение:RoC-2.jpg|thumb|Рис.2. «Хороший» классификатор.]] | ||
| - | + | ROC-кривая показывает зависимость TPR от FPR при варьировании порога <tex>w_0</tex>. | |
| + | Она проходит из точки <tex>(0,0)</tex>, соответствующей максимальному значению <tex>w_0</tex>, в точку <tex>(1,1)</tex>, соответствующую минимальному значению <tex>w_0</tex>. | ||
| - | <tex> | + | При <tex>w_0 \;>\, \max_{1=1..m} f(x_i,w)</tex> все объекты классифицируются как отрицательные, и ошибки возникают на всех положительных объектах, <tex>\textrm{FPR}=0</tex>, <tex>\textrm{TPR}=0</tex>. |
| - | + | При <tex>w_0 \;<\, \min_{1=1..m} f(x_i,w)</tex> все объекты классифицируются как положительные, и ошибки возникают на всех отрицательных объектах, <tex>\textrm{FPR}=1</tex>, <tex>\textrm{TPR}=1</tex>. | |
| - | + | ROC-кривая монотонно не убывает. | |
| + | Чем выше лежит кривая, тем лучше качество классификации. | ||
| - | + | На рисунке 1 приведена ROC-кривая, соответствующая худшему случаю — алгоритму «случайного гадания». | |
| + | На рисунке 2 изображён общий случай. | ||
| + | Лучший случай — это кривая, проходящая через точки <tex>(0,0);\; (0,1);\; (1,1)</tex> | ||
| - | ROC-кривая | + | ''ROC-кривая'' может быть вычислена по любой выборке. Однако ''ROC-кривая'', вычисленная по обучающей выборке, является оптимистично смещённой влево-вверх вследствие [[переобучение|переобучения]]. Величину этого смещения предсказать довольно трудно, поэтому на практике ''ROC-кривую'' всегда оценивают по независомой тестовой выборке. |
| - | + | == Площадь под ROC-кривой AUC == | |
| - | + | Площадь под ROC-кривой AUC (Area Under Curve) является агрегированной характеристикой качества классификации, не зависящей от соотношения цен ошибок. | |
| + | Чем больше значение AUC, тем «лучше» модель классификации. | ||
| + | Данный показатель часто используется для сравнительного анализа нескольких моделей классификации. | ||
| - | == Алгоритм построения | + | == Алгоритм построения ROC-кривой == |
| - | + | Следующий алгоритм строит ROC-кривую за <tex>m</tex> обращений к дискриминантной функции. | |
| - | + | '''Входные данные:''' | |
| - | * | + | * Выборка <tex>X^m</tex> |
| - | * <tex>f( | + | * Функция <tex>f(x,w)</tex> при фиксированном векторе параметров <tex>w</tex>. |
| - | + | '''Результат:''' | |
| - | <tex>\{( | + | * <tex>\{(\textrm{FPR}_i, \textrm{TPR}_i)\}_{i=0}^m </tex> — последовательность из <tex>(m+1)</tex> точек ROC-кривой; |
| + | * <tex>\textrm{AUC}</tex> — площадь под ROC-кривой; | ||
| - | === | + | 1. вычислить количество представителей классов <tex>+1</tex> и <tex>-1</tex> в выборке: |
| + | <tex>m_{-}\;:=\;\sum_{i=1}^m [y_i= -1], \ \ m_+\;:=\;\sum_{i=1}^m [y_i= +1] </tex>; | ||
| + | 2. упорядочить выборку <tex>X^m</tex> по убыванию значений <tex>f(x_i,w)</tex>; | ||
| + | 3. установить начальную точку ROC-кривой: | ||
| + | <tex>(\textrm{FPR}_0,\textrm{TPR}_0)\;:=\;(0,0)</tex>; | ||
| + | <tex>\textrm{AUC}\;:=\;0</tex>; | ||
| + | 4. для всех <tex> i\;:=\;1..m </tex> | ||
| + | если <tex>(y_i = -1)</tex>, то сместиться на один шаг вправо: | ||
| + | <tex>\textrm{FPR}_i\;:=\;\textrm{FPR}_{i-1} + \frac{1}{m_-}; \ \ \textrm{TPR}_i\;:=\;\textrm{TPR}_{i-1}</tex>; | ||
| + | <tex>\textrm{AUC}\;:=\;\textrm{AUC} + \frac{1}{m_-}\textrm{TPR}_i</tex>; | ||
| + | 5. иначе сместиться на один шаг вверх: | ||
| + | <tex>\textrm{FPR}_i\;:=\;\textrm{FPR}_{i-1}; \ \ \textrm{TPR}_i\;:=\;\textrm{TPR}_{i-1} + \frac{1}{m_+}</tex>; | ||
| - | + | == Чувствительность и специфичность == | |
| - | + | Наряду с FPR и TPR используют также показатели ''чувствительности'' и ''специфичности'', которые также изменяются в интервале <tex>[0,1]</tex>: | |
| - | + | * ''чувствительность'' алгоритма <tex>a</tex> совпадает с <tex>\textrm{TPR}</tex>; | |
| - | + | * ''специфичность'' алгоритма <tex>a</tex> определяется как <tex>(1-\textrm{FPR})</tex>. | |
| - | + | <!-- [[Изображение:RoC-3.jpg|thumb|Рис. 3. Чувствительность и специфичность алгоритма на RoC-кривой]]--> | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | Модель с высокой чувствительностью часто дает истинный результат при наличии положительного исхода (обнаруживает положительные примеры). Наоборот, модель с высокой специфичностью чаще дает истинный результат при наличии отрицательного исхода (обнаруживает отрицательные примеры). Если рассуждать в терминах медицинской диагностики, где модель классификации пациентов на больных и здоровых называется ''диагностическим тестом'', то получится следующее: | |
| + | * чувствительный ''диагностический тест'' проявляется в гипердиагностике – максимальном предотвращении пропуска больных; | ||
| + | * специфичный ''диагностический тест'' диагностирует только доподлинно больных. Это важно в случае, когда, например, лечение больного связано с серьезными побочными эффектами и гипердиагностика пациентов нежелательна. | ||
| - | + | == История == | |
| + | |||
| + | Термин ''операционная характеристика приёмника'' (Receiver Operating Characteristic, ROC) пришёл из теории обработки сигналов. | ||
| + | Эту характеристику впервые ввели во время II мировой войны, после поражения американского военного флота в Пёрл Харборе в 1941 году, когда была осознана проблема повышения точности распознавания самолётов противника по радиолокационному сигналу. Позже нашлись и другие применения: медицинская диагностика, приёмочный контроль качества, кредитный скоринг, предсказание лояльности клиентов, и т.д. | ||
== См. также == | == См. также == | ||
| Строка 65: | Строка 107: | ||
== Ссылки == | == Ссылки == | ||
| - | * [http://www.basegroup.ru/library/analysis/regression/logistic/ Логистическая регрессия и | + | * [http://www.basegroup.ru/library/analysis/regression/logistic/ Логистическая регрессия и ROC-анализ] |
* [http://en.wikipedia.org/wiki/ROC_curve RoC-curve (english wikipedia)] | * [http://en.wikipedia.org/wiki/ROC_curve RoC-curve (english wikipedia)] | ||
| - | |||
| - | |||
[[Категория:Классификация]] | [[Категория:Классификация]] | ||
| - | |||
| - | |||
Текущая версия
|
Кривая ошибок или ROC-кривая – графичекая характеристика качества бинарного классификатора, зависимость доли верных положительных классификаций от доли ложных положительных классификаций при варьировании порога решающего правила. Преимуществом ROC-кривой является её инвариантность относительно отношения цены ошибки I и II рода.
Задача классификации
Рассмотрим задачу классификации в случае двух классов, называемых «положительным» и «отрицательным». Обозначим множество классов через . Большинство известных классификаторов могут быть представлены в виде
где
— произвольный объект,
— дискриминантная функция,
— вектор параметров, определяемый по обучающей выборке,
— порог.
Уравнение
определяет разделяющую поверхность.
Примером является линейный классификатор, в котором дискриминантная функция имеет вид скалярного произведения вектора описания объекта на вектор параметров:
.
Пусть – цена ошибки (штраф за ошибку) на объекте класса
.
Для байесовского классификатора при достаточно общих предположениях доказано, что оптимальное значение порога зависит только от соотношения цены ошибок:
тогда как оптимальное значение вектора параметров , наоборот, зависит от выборки и не зависит от цены ошибок.
Таким образом, варьирование порога
для многих классификаторов эквивалентно варьированию отношения цены ошибок на отрицательных и положительных объектах.
На практике цены ошибок зависят от особенностей конкретной задачи (например, от различных экономических соображений или экспертных оценок) и могут многократно пересматриваться.
Заметим, что частным случаем линейного байесовского классификатора является логистическая регрессия.
ROC-кривая наглядно представляет, каким будет качество классификации при различных и фиксированном
.
TPR и FPR
Пусть задана выборка объектов с соответствующими им верными ответами
.
Тогда для классификатора
можно определить две характеристики качества:
- Доля ложных положительных классификаций (False Positive Rate, FPR):
- Доля верных положительных классификаций (True Positive Rate, TPR):
ROC-кривая
ROC-кривая показывает зависимость TPR от FPR при варьировании порога .
Она проходит из точки
, соответствующей максимальному значению
, в точку
, соответствующую минимальному значению
.
При все объекты классифицируются как отрицательные, и ошибки возникают на всех положительных объектах,
,
.
При все объекты классифицируются как положительные, и ошибки возникают на всех отрицательных объектах,
,
.
ROC-кривая монотонно не убывает. Чем выше лежит кривая, тем лучше качество классификации.
На рисунке 1 приведена ROC-кривая, соответствующая худшему случаю — алгоритму «случайного гадания».
На рисунке 2 изображён общий случай.
Лучший случай — это кривая, проходящая через точки
ROC-кривая может быть вычислена по любой выборке. Однако ROC-кривая, вычисленная по обучающей выборке, является оптимистично смещённой влево-вверх вследствие переобучения. Величину этого смещения предсказать довольно трудно, поэтому на практике ROC-кривую всегда оценивают по независомой тестовой выборке.
Площадь под ROC-кривой AUC
Площадь под ROC-кривой AUC (Area Under Curve) является агрегированной характеристикой качества классификации, не зависящей от соотношения цен ошибок. Чем больше значение AUC, тем «лучше» модель классификации. Данный показатель часто используется для сравнительного анализа нескольких моделей классификации.
Алгоритм построения ROC-кривой
Следующий алгоритм строит ROC-кривую за обращений к дискриминантной функции.
Входные данные:
- Выборка
- Функция
при фиксированном векторе параметров
.
Результат:
-
— последовательность из
точек ROC-кривой;
-
— площадь под ROC-кривой;
1. вычислить количество представителей классови
в выборке:
; 2. упорядочить выборку
по убыванию значений
; 3. установить начальную точку ROC-кривой:
;
; 4. для всех
если
, то сместиться на один шаг вправо:
;
; 5. иначе сместиться на один шаг вверх:
;
Чувствительность и специфичность
Наряду с FPR и TPR используют также показатели чувствительности и специфичности, которые также изменяются в интервале :
- чувствительность алгоритма
совпадает с
;
- специфичность алгоритма
определяется как
.
Модель с высокой чувствительностью часто дает истинный результат при наличии положительного исхода (обнаруживает положительные примеры). Наоборот, модель с высокой специфичностью чаще дает истинный результат при наличии отрицательного исхода (обнаруживает отрицательные примеры). Если рассуждать в терминах медицинской диагностики, где модель классификации пациентов на больных и здоровых называется диагностическим тестом, то получится следующее:
- чувствительный диагностический тест проявляется в гипердиагностике – максимальном предотвращении пропуска больных;
- специфичный диагностический тест диагностирует только доподлинно больных. Это важно в случае, когда, например, лечение больного связано с серьезными побочными эффектами и гипердиагностика пациентов нежелательна.
История
Термин операционная характеристика приёмника (Receiver Operating Characteristic, ROC) пришёл из теории обработки сигналов. Эту характеристику впервые ввели во время II мировой войны, после поражения американского военного флота в Пёрл Харборе в 1941 году, когда была осознана проблема повышения точности распознавания самолётов противника по радиолокационному сигналу. Позже нашлись и другие применения: медицинская диагностика, приёмочный контроль качества, кредитный скоринг, предсказание лояльности клиентов, и т.д.