Метод Натаниеля Мейкона (N.Macon) поиска исходных приближений для случая почти равных корней

Материал из MachineLearning.

(Различия между версиями)

Перейти к: навигация, поиск

Текущая версия

Содержание

1 Введение
- 1.1 Метод Ньютона-Рафсона
- 1.2 Случай почти равных корней
2 Изложение метода
- 2.1 Поиск начального приближения
3 Список литературы

Введение

Метод Ньютона-Рафсона

Основная статья: Метод касательных (Ньютона-Рафсона)

Пусть имеется некоторая функция $F(x)$ и необходимо найти такие значения аргумента $x$ , для которых

(1)

$F(x)=0$

Перепишем (1) в виде

(1.1)

$x = f(x)$

и запишем $n+1$ -ое приближения корня (1.1), при этом делая поправку $\alpha$ к очередному значению $x_n$

(2)

$x_{n+1} = x_n + \alpha \Delta x_n,$

где $\Delta x_n = f(x_n) - x_n,$ и положим $\alpha = \frac{1}{1-f'(x_n)}$ .

Тогда (2) перепишется в виде

(3)

$x_{n+1} = \frac{f(x_n) - x_n f'(x_n)}{1 - f'(x_n)}$

Нетрудно видеть, что (3) эквивалентно простому методу последовательных приближений

$x_{n+1} = g(x_n),$

где $g(x) = \frac{f(x) - x f'(x)}{1 - f'(x)}$ .

Вспомним также, что если $|g'(x)| < 1$ , то метод сходится. Имеем

$g'(x) = \frac{f''(x)[f(x) - x]}{[1 - f'(x)]^2}.$

Но так как справедливо соотношение (1.1), то для $x,$ достаточно близких к решению (1.1), выражение в скобках в числителе дроби становится малым. Поэтому итерационный метод, описываемый формулой (3) сходится, если

1. Начальное приближение $x_0$ выбрано достаточно близко к решению $x = f(x)$ .

2. Производная $f''(x)$ не становится слишком большой.

3. Производная $f'(x)$ не слишком близка к 1.

Это и есть метод Ньютона-Рафсона. Обычно его записывают в виде

(4)

$x_{n+1} = x_{n} - \frac{F(x_n)}{F'(x_n)}$ ,

где $F(x) = f(x) - x = 0$

Таким образом, мы вернулись к уравнению в форме (1), и условия сходимости принимают следующий вид

1. Начальное приближение $x_0$ выбрано достаточно близко к корню уравнения $F(x) = 0$ .

2. Производная $F''(x)$ не становится очень большой.

3. Производная $F'(x)$ не слишком близка к 0.

Случай почти равных корней

Рисунок 1

Условие 3 сходимости метода Ньютона-Рафсона означает, что никакие два корня не находятся слишком близко один к другому. Соответствующая ситуация представлена на рисунке 1 (масштаб сильно увеличен). Заметим, что производная $f'(x)$ близка к 1 при x, равном обоим значениям корней, $a_1$ и $a_2$ . Более того, на основании теоремы Лагранжа, можно утверждать, что $f'(x) = 1$ где-то между $a_1$ и $a_2$ .

Рассмотрим, что случится, если принять $x_0$ в качестве исходного значения для корня $a_1$ . Касательная, проведенная через точку $C$ , пересечет прямую $y=x$ в точке $A$ , и следующее приближение будет равно $x_1$ . Касательная, проведенная через точку $B$ , пересекает прямую в точке $D$ , и в качестве следующего приближеня получается снова $x_0$ . Итерационный процесс, таким образом, осциллирует между $x_0$ и $x_1$ до бесконечности, не сходясь ни к одному значению корня. Иначе говоря, не удается отделить эти два корня, потому что они расположены слишком близко.

Поэтому необходимо начальное приближение, достаточно близкое к искомому значению корня. Трудности возникают потому, что вычисление знаменателя в формуле (3) включает в себя вычитание двух почти равных чисел, что приводит к понижению точности.

Изложение метода

Поиск начального приближения

Рисунок 2

Сначала находится значение x, при котором $f'(x)=1$ , то есть решается уравнение

$x=x+f'(x)-1$

Пусть решением этого уравнения будет некоторое $x = x_0$ . Эта точка расположена между двумя корнями, $a_1$ и $a_2$ . Чтобы получить начальное приближение для решения уравнения, предположим, что $x_0$ лежит посредине между $a_1$ и $a_2$ (рисунок 2). Другими словами, мы предполагаем, что $x_0 + d$ и $x_0 - d$ являются корнями уравнения (1.1). Разлагая $f(x)$ в ряд Тейлора в окрестности точки $x_0$ и принимая во внимание, что $f'(x)=1$ , получаем

$f(x) = f(x_0) + (x - x_0) + \frac{1}{2} f''(x_0) (x - x_0)^2 + \ldots$

Ограничим ряд тремя членами. Подставляя $x + d$ вместо $x$ , имеем

$f(x_0+d) = f(x_0) + d + \frac{1}{2} f''(x_0)(d^2)$

Но по условию

$f(x_0+d) = x_0+d,$

поэтому, решая эти уравнения относительно $d$ , получаем

$d=\sqrt{\frac{2(x_0 - f(x_0))}{f''(x_0)}}$

Таким образом, процесс решения сводится к следующему. Если дано уравнение с почти равными корнями, то, определив приблизительное местонахождение этих корней, необходиом решить уравнение

$x = x + f'(x) - 1$

и определить значение $x_0$ . Для решения этого уравнения можно применить, например, метод Ньютона-Рафсона. Найдя значение $x_0$ , можно определить значение $d$ . И, наконец, значения $x_0-d$ и $x_0+d$ используются в качестве начальных приближений для определения соответственно $a_1$ и $a_2$ .

Список литературы

Мак-Кракен Д. Дорн У. Численные методы и программирование на ФОРТРАНе М.: Мир, 1977.

Это незавершённая статья. Вы поможете проекту, исправив и дополнив её.

Источник — «http://www.machinelearning.ru/wiki/index.php?title=%D0%9C%D0%B5%D1%82%D0%BE%D0%B4_%D0%9D%D0%B0%D1%82%D0%B0%D0%BD%D0%B8%D0%B5%D0%BB%D1%8F_%D0%9C%D0%B5%D0%B9%D0%BA%D0%BE%D0%BD%D0%B0_%28N.Macon%29_%D0%BF%D0%BE%D0%B8%D1%81%D0%BA%D0%B0_%D0%B8%D1%81%D1%85%D0%BE%D0%B4%D0%BD%D1%8B%D1%85_%D0%BF%D1%80%D0%B8%D0%B1%D0%BB%D0%B8%D0%B6%D0%B5%D0%BD%D0%B8%D0%B9_%D0%B4%D0%BB%D1%8F_%D1%81%D0%BB%D1%83%D1%87%D0%B0%D1%8F_%D0%BF%D0%BE%D1%87%D1%82%D0%B8_%D1%80%D0%B0%D0%B2%D0%BD%D1%8B%D1%85_%D0%BA%D0%BE%D1%80%D0%BD%D0%B5%D0%B9»

Категория: Незавершённые статьи

@@ Строка 1: / Строка 1: @@
 == Введение ==
+=== Метод Ньютона-Рафсона ===
+{{main|Метод касательных (Ньютона-Рафсона)}}
+Пусть имеется некоторая функция <tex>F(x)</tex> и необходимо найти такие значения аргумента <tex>x</tex>, для которых
+{{eqno|1}}
+:<tex>F(x)=0</tex>
+Перепишем {{eqref|1}} в виде
+{{eqno|1.1}}
+:<tex>x = f(x)</tex>
+и запишем <tex>n+1</tex>-ое приближения корня {{eqref|1.1}}, при этом делая поправку <tex>\alpha</tex> к очередному значению <tex>x_n</tex>
+{{eqno|2}}
+:<tex>x_{n+1} = x_n + \alpha \Delta x_n,</tex>
+где <tex>\Delta x_n = f(x_n) - x_n,</tex> и положим <tex>\alpha = \frac{1}{1-f'(x_n)}</tex>.
+Тогда {{eqref|2}} перепишется в виде
+{{eqno|3}}
+:<tex>x_{n+1} = \frac{f(x_n) - x_n f'(x_n)}{1 - f'(x_n)}</tex>
+Нетрудно видеть, что {{eqref|3}} эквивалентно простому [[Метод последовательных приближений|методу последовательных приближений]]
+:<tex>x_{n+1} = g(x_n),</tex>
+где <tex>g(x) = \frac{f(x) - x f'(x)}{1 - f'(x)}</tex>.
+Вспомним также, что если <tex>|g'(x)| < 1</tex>, то метод сходится. Имеем
+:<tex>g'(x) = \frac{f''(x)[f(x) - x]}{[1 - f'(x)]^2}.</tex>
+Но так как справедливо соотношение {{eqref|1.1}}, то для <tex>x,</tex> достаточно близких к решению {{eqref|1.1}}, выражение в скобках в числителе дроби становится малым. Поэтому итерационный метод, описываемый формулой {{eqref|3}} сходится, если
+:1. Начальное приближение <tex>x_0</tex> выбрано достаточно близко к решению <tex>x = f(x)</tex>.
+:2. Производная <tex>f''(x)</tex> не становится слишком большой.
+:3. Производная <tex>f'(x)</tex> не слишком близка к 1.
+Это и есть метод Ньютона-Рафсона. Обычно его записывают в виде
+{{eqno|4}}
+:<tex>x_{n+1} = x_{n} - \frac{F(x_n)}{F'(x_n)}</tex>,
+где <tex>F(x) = f(x) - x = 0</tex>
+Таким образом, мы вернулись к уравнению в форме {{eqref|1}}, и условия сходимости принимают следующий вид
+:1. Начальное приближение <tex>x_0</tex> выбрано достаточно близко к корню уравнения <tex>F(x) = 0</tex>.
+:2. Производная <tex>F''(x)</tex> не становится очень большой.
+:3. Производная <tex>F'(x)</tex> не слишком близка к 0.
+=== Случай почти равных корней ===
+[[Изображение:macon.png|thumb|200px|Рисунок 1]]
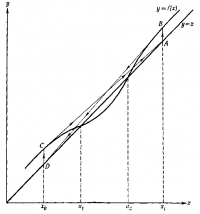
+Условие 3 сходимости метода Ньютона-Рафсона означает, что никакие два корня не находятся слишком близко один к другому. Соответствующая ситуация представлена на рисунке 1 (масштаб сильно увеличен). Заметим, что производная <tex>f'(x)</tex> близка
+к 1 при x, равном обоим значениям корней, <tex>a_1</tex> и <tex>a_2</tex>. Более того, на основании теоремы Лагранжа, можно утверждать, что <tex>f'(x) = 1</tex> где-то между <tex>a_1</tex> и <tex>a_2</tex>.
+Рассмотрим, что случится, если принять <tex>x_0</tex> в качестве исходного значения для корня <tex>a_1</tex>. Касательная,
+проведенная через точку <tex>C</tex>, пересечет прямую <tex>y=x</tex> в точке <tex>A</tex>, и следующее приближение будет равно
+<tex>x_1</tex>. Касательная, проведенная через точку <tex>B</tex>, пересекает прямую в точке <tex>D</tex>, и в качестве следующего приближеня получается снова <tex>x_0</tex>. Итерационный процесс, таким образом, осциллирует между <tex>x_0</tex> и <tex>x_1</tex>
+до бесконечности, не сходясь ни к одному значению корня. Иначе говоря, не удается <i>отделить</i> эти два корня, потому что они расположены слишком близко.
+Поэтому необходимо начальное приближение, достаточно близкое к искомому значению корня. Трудности возникают потому, что
+вычисление знаменателя в формуле {{eqref|3}} включает в себя вычитание двух почти равных чисел, что приводит к понижению точности.
 == Изложение метода ==
-== Анализ метода ==
-== Числовой пример ==
+=== Поиск начального приближения ===
-== Заключение ==
-== Литература ==
+[[Изображение:macon2.PNG|thumb|200px|Рисунок 2]]
+Сначала находится значение x, при котором <tex>f'(x)=1</tex>, то есть решается уравнение
+:<tex>x=x+f'(x)-1</tex>
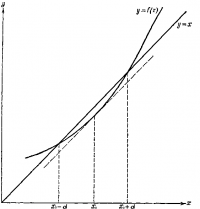
+Пусть решением этого уравнения будет некоторое <tex>x = x_0</tex>. Эта точка расположена между двумя корнями, <tex>a_1</tex> и <tex>a_2</tex>. Чтобы получить начальное приближение для решения уравнения, предположим, что <tex>x_0</tex> лежит посредине между
+<tex>a_1</tex> и <tex>a_2</tex> (рисунок 2). Другими словами, мы предполагаем, что <tex>x_0 + d</tex> и <tex>x_0 - d</tex> являются корнями уравнения {{eqref|1.1}}. Разлагая <tex>f(x)</tex> в ряд Тейлора в окрестности точки <tex>x_0</tex> и принимая во внимание, что <tex>f'(x)=1</tex>, получаем
+:<tex>f(x) = f(x_0) + (x - x_0) + \frac{1}{2} f''(x_0) (x - x_0)^2 + \ldots</tex>
+Ограничим ряд тремя членами. Подставляя <tex>x + d</tex> вместо <tex>x</tex>, имеем
+:<tex>f(x_0+d) = f(x_0) + d + \frac{1}{2} f''(x_0)(d^2)</tex>
+Но по условию
+:<tex>f(x_0+d) = x_0+d,</tex>
+поэтому, решая эти уравнения относительно <tex>d</tex>, получаем
+:<tex>d=\sqrt{\frac{2(x_0 - f(x_0))}{f''(x_0)}}</tex>
+Таким образом, процесс решения сводится к следующему. Если дано уравнение с почти равными корнями, то, определив приблизительное
+местонахождение этих корней, необходиом решить уравнение
+:<tex>x = x + f'(x) - 1</tex>
+и определить значение <tex>x_0</tex>. Для решения этого уравнения можно применить, например, метод Ньютона-Рафсона.
+Найдя значение <tex>x_0</tex>, можно определить значение <tex>d</tex>. И, наконец, значения <tex>x_0-d</tex> и <tex>x_0+d</tex>
+используются в качестве начальных приближений для определения соответственно <tex>a_1</tex> и <tex>a_2</tex>.
+== Список литературы ==
+* ''Мак-Кракен Д.''&nbsp; ''Дорн У.'' Численные методы и программирование на ФОРТРАНе М.: Мир, 1977.
+{{Stub|}}

Метод Натаниеля Мейкона (N.Macon) поиска исходных приближений для случая почти равных корней

Материал из MachineLearning.

Текущая версия

Содержание

Введение

Метод Ньютона-Рафсона

Случай почти равных корней

Изложение метода

Поиск начального приближения

Список литературы

Просмотры

Личные инструменты

Навигация

Поиск

Инструменты