Метод покоординатного спуска
Материал из MachineLearning.
| Строка 1: | Строка 1: | ||
| - | == | + | == Введение == |
Рассмотрим задачу поиска минимума функции <tex>f(x): \mathbb{R}^n \to \mathbb{R} </tex>, записываемую в виде: | Рассмотрим задачу поиска минимума функции <tex>f(x): \mathbb{R}^n \to \mathbb{R} </tex>, записываемую в виде: | ||
{{eqno|1}} | {{eqno|1}} | ||
::<tex>f(x) \to \min_{x \in \mathbb{R}^n}</tex> | ::<tex>f(x) \to \min_{x \in \mathbb{R}^n}</tex> | ||
| - | == Метод покоординатного спуска | + | В этой статье описан метод покоординатного спуска, решающий поставленную задачу. Также приведена теорема сходимости метода покоординатного спуска. |
| + | |||
| + | == Метод покоординатного спуска == | ||
===Алгоритм=== | ===Алгоритм=== | ||
| Строка 18: | Строка 20: | ||
#*# фиксируем значения всех переменных кроме <tex>x_i</tex>, получая одномерную функцию <tex>f(x_i)</tex> | #*# фиксируем значения всех переменных кроме <tex>x_i</tex>, получая одномерную функцию <tex>f(x_i)</tex> | ||
#*# проводим одномерную оптимизацию по переменной <tex>x_i</tex>, любым методом одномерной оптимизации | #*# проводим одномерную оптимизацию по переменной <tex>x_i</tex>, любым методом одномерной оптимизации | ||
| - | #*# если выполен критерий останова, то возвращаем текущее значение <tex>x=(x_1,\dots,x_n)</tex> | + | #*# если выполен критерий останова (варианты описаны ниже), то возвращаем текущее значение <tex>x=(x_1,\dots,x_n)</tex> |
===Критерий останова=== | ===Критерий останова=== | ||
| Строка 38: | Строка 40: | ||
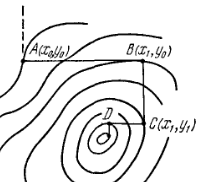
'''Теорема о сходимости метода покоординатного спуска.''' | '''Теорема о сходимости метода покоординатного спуска.''' | ||
| - | Для простоты рассмотрим функцию двух переменных <tex>f(x,y)</tex>. Выберем некоторое | + | Для простоты рассмотрим функцию двух переменных <tex>f(x,y)</tex>. Выберем некоторое начальное приближение <tex>(x_0,y_0)</tex> и проведем линию уровня через эту точку. Пусть в области <tex>G</tex>, ограниченной этой линией уровня, выполняются неравенства, означающий положительную определенность квадратичной формы: |
::<tex>f_{xx}''\geq a>0,\; f_{yy}''\geq b>0,\; |f_{xy}''|\leq c,\; ab>c^2.</tex> | ::<tex>f_{xx}''\geq a>0,\; f_{yy}''\geq b>0,\; |f_{xy}''|\leq c,\; ab>c^2.</tex> | ||
Тогда спуск по координатам сходится к минимуму из данного начального приближения, причем линейно. | Тогда спуск по координатам сходится к минимуму из данного начального приближения, причем линейно. | ||
| Строка 57: | Строка 59: | ||
== Рекомендации программисту == | == Рекомендации программисту == | ||
| - | + | Возникающую одномерную задачу оптимизации можно решать любым методом одномерной оптимизации, например [[Метод золотого сечения. Симметричные методы|методом золотого сечения]]. | |
== Заключение == | == Заключение == | ||
Версия 17:10, 3 декабря 2008
Содержание |
Введение
Рассмотрим задачу поиска минимума функции , записываемую в виде:
В этой статье описан метод покоординатного спуска, решающий поставленную задачу. Также приведена теорема сходимости метода покоординатного спуска.
Метод покоординатного спуска
Алгоритм
Вход: функция
Выход: найденная точка оптимума
- Инициализация некоторым значением
- повторять:
- для
- фиксируем значения всех переменных кроме
, получая одномерную функцию
- проводим одномерную оптимизацию по переменной
, любым методом одномерной оптимизации
- если выполен критерий останова (варианты описаны ниже), то возвращаем текущее значение
- фиксируем значения всех переменных кроме
- для
Критерий останова
Критерии остановки процесса приближенного нахождения минимума могут быть основаны на различных соображениях. Некоторые из них:
Здесь - значение, полученное после
-го шага оптимизации.
- наперед заданное положительное число.
Сходимость метода
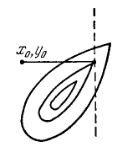
Легко убедится, что существуют функции, когда метод координатного спуска не приводит даже в локальный оптимум.
Пусть линии уровня образуют истинный овраг (рис.2), когда спуск по любой координате приводит на <<дно>> оврага, а любое движение по следующей координате (пунктирная линия) ведет на подъем. Никакой дальнейший спуск по координатам в данном случае невозможен, хотя минимум еще не достигнут.
Теорема о сходимости метода покоординатного спуска.
Для простоты рассмотрим функцию двух переменных . Выберем некоторое начальное приближение
и проведем линию уровня через эту точку. Пусть в области
, ограниченной этой линией уровня, выполняются неравенства, означающий положительную определенность квадратичной формы:
Тогда спуск по координатам сходится к минимуму из данного начального приближения, причем линейно.
Числовые примеры
Для исследования сходимости метода покоординатного спуска была выбрана функция:
.
Начальное приближение - точка (10,10). Использован критерий останова:
Для решения одномерных задач оптимизации использован метод золотого сечения.
Метод получил точность 1e-8 за 7 итераций.
Отсюда можно сделать вывод, что метод координатного спуска сходится неплохо на примерах, для которых он применим.
Рекомендации программисту
Возникающую одномерную задачу оптимизации можно решать любым методом одномерной оптимизации, например методом золотого сечения.
Заключение
Метод координатного спуска является простым в реализации методом оптимизации. Главным недостатком метода является его ограниченная применимость.
Ссылки
Список литературы
- А.А.Самарский, А.В.Гулин. Численные методы. Москва «Наука», 1989.
- Н.С.Бахвалов, Н.П.Жидков, Г.М.Кобельков. Численные методы. Лаборатория Базовых Знаний, 2003.
- Н.Н.Калиткин. Численные методы. Москва «Наука», 1978.