Модель Тригга-Лича

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск
Строка 59: Строка 59:
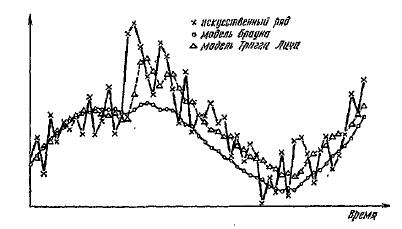
На рис. 3 линия, обозначенная крестиками, показывает те же случайные данные, но с синусоидальным колебанием с периодом 52 (52 недели в году).
На рис. 3 линия, обозначенная крестиками, показывает те же случайные данные, но с синусоидальным колебанием с периодом 52 (52 недели в году).
 +
Через 15 интервалов возникает ступенчатое изменение и отмеченная кружками линия показывает реакцию модели
 +
 +
::<tex>\hat x_\tau(t)=\hat a_{1,t}+\hat a_{2,t}\tau+\hat a_{3,t}sin{}</tex>.
{{Задание|Коликова Катя|Vokov|31 декабря 2009}}
{{Задание|Коликова Катя|Vokov|31 декабря 2009}}

Версия 14:41, 27 декабря 2009

Введение

Модель Тригга-Лича применяется в адаптивных методах прогнозирования временных рядов.

Модель Тригга-Лича относится к моделям с адаптивными параметрами адаптациями, то есть, является моделью с повышенной способностью к самообучению.

А. Триггом и А. Личем было предложено модифицировать предсказывающие системы, использующие экспоненциальное сглаживание, посредствои изменения скорости реакции в зависимости от величины контнольного сигнала. В простейшей модели это эквивалентно регулированию параметра сглаживания \alpha. Наиболее очевидный способ заставить систему автоматически реагировать на расхождение прогнозов и фактических данных - это увеличение \alpha с тем, чтобы придать больший вес свежим данным и, таким образом, обеспечить более быстрое приспособление модели к новой ситуации. Как только система приспособилась, необходимо опять уменьшить величину \alpha для фильтрации шума.

Простой способ достижения такой адаптивной скорости состоит в выборе

\alpha_t=|K_t|,

где K_t - скользящий контрольный сигнал.

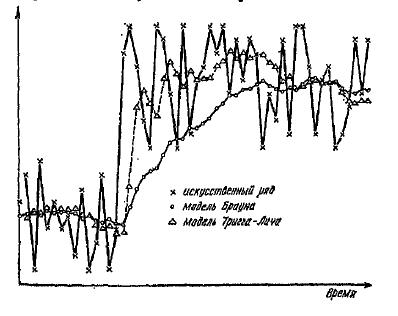
Рис. 1. Сравнение реакций полиномиальных моделей нулевого порядка Брауна () и Тригга-Лича на ступенчатое изменение уровня ряда,
Рис. 1. Сравнение реакций полиномиальных моделей нулевого порядка Брауна (\beta=0,9) и Тригга-Лича на ступенчатое изменение уровня ряда, \tau=1
Рис. 2. Сравнение реакций на линейное изменение уровня ряда полиномиальных моделей первого порядка Брауна и Тригга-Лича,
Рис. 2. Сравнение реакций на линейное изменение уровня ряда полиномиальных моделей первого порядка Брауна и Тригга-Лича, \beta^2=0,9, \; \tau=1
Рис. 3. Сравнение моделей Брауна и Тригга-Лича,
Рис. 3. Сравнение моделей Брауна и Тригга-Лича, n=4; \; \beta^n=0,9, \; \tau=1

На рис.1 показано испытание полиномиальной модели нулевого порядка с переменным параметром \alpha при прогнозировании искусственного ряда.

Крестики на рисунке отражают значения членов временного ряда, в котором наблюдается изменение ступенчатого типа. Ряд искусственно генерирован по модели

x_t=a'_1+\eps_t, при t<t_1;
x_t=a''_1+\eps_t, при t>t_1;
a'_1=const;
a'_1=const;
a'_1\ne a''_1,

где \eps_t - неавтокоррелирванные случайные нормальные отклонения с нулевым математическим ожиданием и дисперсией \sigma_2.

Реакция простейшей модели экспоненциального типа с постоянным коэффициентом сглаживания \alpha=0,1 отмечена кружками. Пунктирная линия характеризует реакцию подобной же системы, но с переменным \alpha_t. Можно видеть, что система с адаптивным \alpha приспосабливается к ступенчатым изменениям намного быстрее, а после отработки ступеньки размах ее колебаний не больше, чем у обычной системы, поскольку контрольный сигнал, построенный по принципу сглаженной ошибки, остается большим, как правило, только пока прогнозирующая система находится в переходном режиме. Аналогичная модификация возможна и для более сложных моделей. Рассмотрим частный случай обобщенной модели Р.Брауна (модель Брауна) - модель линейного роста (n=2)

\hat x_\tau(t)=\hat a_{1,t}+\hat a_{2,t}\tau,

для которой уравнения обновления коэффицинтов будут:

\hat a_{1,t}=\hat a_{1,t-1}+\hat a_{2,t-1}+(1-\beta^2)\eps_1(t-1);
\hat a_{2,t}=\hat a_{2,t-1}+(1-\beta)^2\eps_1(t-1).

Из уравнений видно, что оценка среднего уровня процесса \hat a_1 реагирует на ошибку прогноза со скоростью (1-\beta^2). В моделях Р.Брауна с n параметрами скорость реакции определяется величиной (1-\beta^n), называемой эквивалентной постоянной сглаживания.

В многопараметрической модели Р.Брауна представляется естественным приравнять эквивалентную постоянную сглаживания модулю контрольного сигнала. В линейной модели мы могли бы положить

(1-\beta^2_t)=|K_t|,

откуда

\beta_t=\sqr{1-|K_t|}.

Это означало бы, что каждый элемент вектора h как функции от \beta каждый раз претерпевает соответствующие изменения. Однако эксперименты показали, что зависимость всех элементов h_i от контрольного сигнала ухудшает прогноз, делая его неустойчивым. Если же ограничить модификацию вектора h только его первой составляющей h_1, то эксперимент показывает, что во всех случаях такая система приводит к более стабильным результатам.

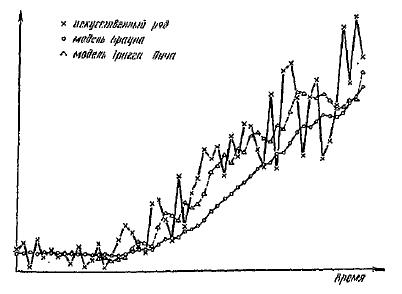
На рис. 2 показан ряд с линейной тенденцией роста, на который наложены те же случайные данные, что и на рис. 1. В этом примере среднеквадратичное отклонение шума взято пропорциональным среднему уровню ряда. Реакция, соответствующая прогнозу на один шаг вперед обычной модели линейного роста с эквивалентной постоянной (1-\beta^2)=0,1, отмечена кружками. Прогнозы аналогичной модели, но с h_1=|K_t| показаны пунктиром.

На рис. 3 линия, обозначенная крестиками, показывает те же случайные данные, но с синусоидальным колебанием с периодом 52 (52 недели в году).

Через 15 интервалов возникает ступенчатое изменение и отмеченная кружками линия показывает реакцию модели

\hat x_\tau(t)=\hat a_{1,t}+\hat a_{2,t}\tau+\hat a_{3,t}sin{}.



Данная статья является непроверенным учебным заданием.
Студент: Участник:Коликова Катя
Преподаватель: Участник:Vokov
Срок: 31 декабря 2009

До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru. По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}.

См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.


Источник — «http://www.machinelearning.ru/wiki/index.php?title=%D0%9C%D0%BE%D0%B4%D0%B5%D0%BB%D1%8C_%D0%A2%D1%80%D0%B8%D0%B3%D0%B3%D0%B0-%D0%9B%D0%B8%D1%87%D0%B0»
Личные инструменты