Кривая ошибок
Материал из MachineLearning.
м |
(дополнение) |
||
| Строка 24: | Строка 24: | ||
Подробнее об этих функционалах можно прочесть [http://en.wikipedia.org/wiki/ROC_curve#Basic_concept здесь]. | Подробнее об этих функционалах можно прочесть [http://en.wikipedia.org/wiki/ROC_curve#Basic_concept здесь]. | ||
| + | |||
| + | [[Изображение:RoC-1.jpg|thumb|Рис.1. «Случайное гадание»]] [[Изображение:RoC-2.jpg|thumb|Рис.2. Хороший случай]] | ||
ROC-кривая показывает зависимость количества верно классифицированных положительных объектов из <tex>X^l</tex> (по оси Y) от количества неверно классифицированных отрицательных объектов из <tex>X^l</tex> (по оси X). | ROC-кривая показывает зависимость количества верно классифицированных положительных объектов из <tex>X^l</tex> (по оси Y) от количества неверно классифицированных отрицательных объектов из <tex>X^l</tex> (по оси X). | ||
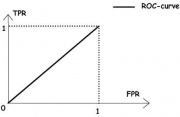
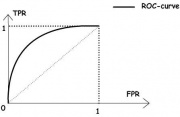
| - | + | На рисунке 1 приведена RoC-кривая, соответствующая алгоритму «случайного гадания», когда классификация объекта происходит методом «подбрасывания монетки» с вероятностью исходов <tex>\frac12</tex>. На рисунке 2 изображён общий случай. | |
| + | |||
| + | Визуально, чем выше лежит кривая, тем лучше характеристики качества алгоритма. | ||
| - | |||
== Алгоритм построения RoC-кривой == | == Алгоритм построения RoC-кривой == | ||
| Строка 56: | Строка 59: | ||
== Функционал качества == | == Функционал качества == | ||
| - | В качестве функционала качества, инвариантного относительно выбора цен ошибок, используют площадь под RoC-кривой. Эту величину также называют AUC (Area Under Curve). Чем больше значение AUC, тем «лучше» алгоритм. | + | В качестве функционала качества, инвариантного относительно выбора цен ошибок, используют площадь под RoC-кривой. Эту величину также называют AUC (Area Under Curve). Чем больше значение AUC, тем «лучше» алгоритм. Данный показатель предназначен скорее для сравнительного анализа нескольких моделей, не предоставляя полезной информации о конкретном классификаторе. |
| + | |||
| + | Намного большую информацию о ценности бинарного классификатора несут в себе такие показатели, как ''чувствительность'' и ''специфичность'': | ||
| + | [[Изображение:RoC-3.jpg|thumb|Рис. 3. Чувствительность и специфичность алгоритма на RoC-кривой]] | ||
| + | |||
| + | * ''Чувствительность'' алгоритма — совпадает с True Positive Rate <tex>(TPR)</tex>, изменяется в интервале <tex>[0,1]</tex>; | ||
| + | * ''Специфичность'' алгоритма — вводится, как <tex>(1-FPR)</tex>, и также изменяется в интервале <tex>[0,1]</tex>. | ||
| + | |||
| + | Идеальный случай — когда значения показателей чувствительности и специфичности близки к 1, однако на практике это достигается редко. | ||
| + | |||
| + | Модель с высокой чувствительностью часто дает истинный результат при наличии положительного исхода (обнаруживает положительные примеры). Наоборот, модель с высокой специфичностью чаще дает истинный результат при наличии отрицательного исхода (обнаруживает отрицательные примеры). Если рассуждать в терминах медицины – задачи диагностики заболевания, где модель классификации пациентов на больных и здоровых называется ''диагностическим тестом'', то получится следующее: | ||
| + | * Чувствительный ''диагностический тест'' проявляется в гипердиагностике – максимальном предотвращении пропуска больных; | ||
| + | * Специфичный ''диагностический тест'' диагностирует только доподлинно больных. Это важно в случае, когда, например, лечение больного связано с серьезными побочными эффектами и гипердиагностика пациентов нежелательна. | ||
== См. также == | == См. также == | ||
Версия 18:19, 19 января 2010
Кривая ошибок или ROC-кривая – часто применяемый способ представления характеристик качества бинарного классификатора.
Содержание |
Кривая ошибок в задаче классификации
Рассмотрим задачу логистической регрессии в случае двух классов. Традиционно, один из этих классов будем называть классом «с положительными исходами», другой - «с отрицательными исходами» и обозначим множество классов через . Рассмотрим линейный классификатор для указанной задачи:
.
Параметр полагается равным
, где
– штраф за ошибку на объекте класса
,
. Эти параметры выбираются из эмперических соображений и зависят от задачи.
Нетрудно заметить, что в задаче существенны не сами параметры , а их отношение:
.
RoC-кривая является распространённым способом оценки качества алгоритма, вне зависимости от выбора цен ошибок.
TPR и FPR
Рассмотрим два следующих функционала:
1. False Positive Rate доля объектов выборки ошибочно отнесённых алгоритмом
к классу {+1}:
2. True Positive Rate доля объектов выборки правильно отнесённых алгоритмом
к классу {+1}:
Подробнее об этих функционалах можно прочесть здесь.
ROC-кривая показывает зависимость количества верно классифицированных положительных объектов из (по оси Y) от количества неверно классифицированных отрицательных объектов из
(по оси X).
На рисунке 1 приведена RoC-кривая, соответствующая алгоритму «случайного гадания», когда классификация объекта происходит методом «подбрасывания монетки» с вероятностью исходов . На рисунке 2 изображён общий случай.
Визуально, чем выше лежит кривая, тем лучше характеристики качества алгоритма.
Алгоритм построения RoC-кривой
На основе обучающей выборки можно очень эффективно аппроксимировать RoC-кривую для заданного классификатора. Ниже приведён алгоритм, строящий эту зависимость.
Входные данные
- Обучающая выборка
-
— вероятность того, что
принадлежит классу {+1}.
Результат
— последовательность из
точек на координатной плоскости из области
, аппроксимирующая RoC-кривую по обучающей выборке
.
Описание алгоритма
1. Вычислим количество представителей классов {+1} и {-1} в обучающей выборке:
![l_-:= \sum_{i=1}^l [y_i= -1], \ l_+:= \sum_{i=1}^l [y_i= +1]](../mimetex/?l_-:= \sum_{i=1}^l [y_i= -1], \ l_+:= \sum_{i=1}^l [y_i= +1] ) ;
2. Упорядочим выборку
;
2. Упорядочим выборку 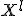 по убыванию значения
по убыванию значения ) ;
3. Начальная точка кривой —
;
3. Начальная точка кривой — :=(0,0)) ;
4. Повторять для всех
;
4. Повторять для всех 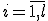 :
Если
:
Если ) , то сместиться вправо:
, то сместиться вправо:
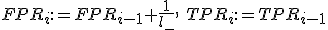 ;
иначе сместиться вверх:
;
иначе сместиться вверх:
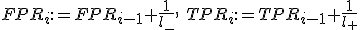 ;
;
Функционал качества
В качестве функционала качества, инвариантного относительно выбора цен ошибок, используют площадь под RoC-кривой. Эту величину также называют AUC (Area Under Curve). Чем больше значение AUC, тем «лучше» алгоритм. Данный показатель предназначен скорее для сравнительного анализа нескольких моделей, не предоставляя полезной информации о конкретном классификаторе.
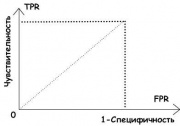
Намного большую информацию о ценности бинарного классификатора несут в себе такие показатели, как чувствительность и специфичность:
- Чувствительность алгоритма — совпадает с True Positive Rate
, изменяется в интервале
;
- Специфичность алгоритма — вводится, как
, и также изменяется в интервале
.
Идеальный случай — когда значения показателей чувствительности и специфичности близки к 1, однако на практике это достигается редко.
Модель с высокой чувствительностью часто дает истинный результат при наличии положительного исхода (обнаруживает положительные примеры). Наоборот, модель с высокой специфичностью чаще дает истинный результат при наличии отрицательного исхода (обнаруживает отрицательные примеры). Если рассуждать в терминах медицины – задачи диагностики заболевания, где модель классификации пациентов на больных и здоровых называется диагностическим тестом, то получится следующее:
- Чувствительный диагностический тест проявляется в гипердиагностике – максимальном предотвращении пропуска больных;
- Специфичный диагностический тест диагностирует только доподлинно больных. Это важно в случае, когда, например, лечение больного связано с серьезными побочными эффектами и гипердиагностика пациентов нежелательна.
См. также
Ссылки
| | Данная статья является непроверенным учебным заданием.
До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru. По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}. См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе. |