Аппроксимация Лапласа (пример)

Материал из MachineLearning.

(Различия между версиями)

Версия 02:36, 23 ноября 2010

Аппроксимация Лапласа - способ оценки параметров нахождения нормального распределения при апроксимации заданой плотности вероятности.

Содержание

1 Сэмплирование
2 Постановка задачи
3 Описание алгоритма
4 Вычислительный эксперимент
- 4.1 Пример 1
5 Смотри также
6 Литература
7 Примечания

Сэмплирование

Сэмплирование – метод выбора подмножества наблюдаемых величин из данного множества, с целью выделения неких свойст исходного множества. Одно из основных приминений методов сэмплирования заключается в оценке математического ожидания сложных вероятностных распределений:

$E[f]=\int f(z)p(z) dz$

для которых данный инеграл не может быть подсчитан аналитическим методом (к примеру, ввиду сложного аналитического вида распределения $p(z)$ ). Однако, можно подсчитать значение p(z) в любой точке z. Основная идея заключается в создании незавсимой выборки $z^{(l)}$ (где $l=1,...,L$ ) из распределения $p(z)$ . Это позволит оцениваемое математическое ожидание приблизить конечной суммой:

$\hat f=\frac{1}{L}\sum_{l=1}^{L} f(z^{(l)})$

Существует несколько методов сэмплирования для создания выборки $z^{(l)}$ ^[1]:

Simple random sampling;
Systematic sampling;
Rejection sampling;
Adaptive rejection sampling.

Постановка задачи

Задана выборка — множество $X^N=\{{x}_1,\ldots,{x}_N|x\in\R^M\}$ значений свободных переменных и множество $\{y_1,\ldots, y_N| y\in\R\}$ соответствующих им значений зависимой переменной. Необходимо для выбранной регрессионной модели $f(\mathbf{w},\mathbf{x})$ :

показать зависимость среднеквадратичной ошибки от значений параметров модели: $SSE=SSE(w)$ ;
построить график и сделать апроксимацию Лапласа для нее;
найти расстояния между получеными зависимостями, используя расстояние Кульбака - Лейблера.

Описание алгоритма

Расстояние Кульбака - Лейблера:

$D_{kl}(p,q)=\sum\limits_{x\in \mathcal{X}} p(x) \ln \frac{p(x)}{q(x)}$

Вычислительный эксперимент

Обозначим плоность распределения SSE как $p_{SSE}$ , а его апроксимация лапласса $p_{lap}$ . При востановлении регрессии рассматривалась следующая гипотеза порождения данных:

$y=f(x,w)$

В таком случае, при фиксированной модели f плотность вероятности появления данных равняется:

$p(y|x,w)=\frac{1}{Z_D}exp(-E_D)$ , где

$E_D$ - это функция регрессионных невязок;

$Z_D$ - нормировачный коэффициент.

Однако, во время вычислительного эксперимента SSE принимало достаточно большие значения (порядка $10^3 - 10^4$ ). Как следствие, p(y|x,w) принимало значения порядка 1, и апроксимация Лапласса была некоректной. Поэтому, апроксимация Лапласса применялась не к самому распределению p(y|x,w), а к ln(p(y|x,w)) (т.е. к -SSE c точностью до коэффициента).

Пример 1

Задуманная функция $y=x + sin3x$ . Берем линейную регрессионную модель с двумя параметрами: $y(x)=w_1+w_2x$ . Используя метод наименьших квадратов находим оптимальное значение $w_1_{opt}$ и $w_2_{opt}$ (при которых SSE минимально).

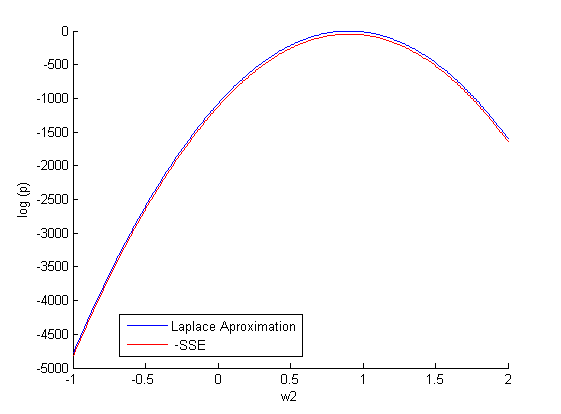
При фиксированном $w_1=w_1_{opt}$ задаем различные значение $w_2$ (500 случайных значений на отрезке [-1;2]) и строим зависимость:

$D_{kl}(p_{SSE},p_{lap})=0.0085$ .

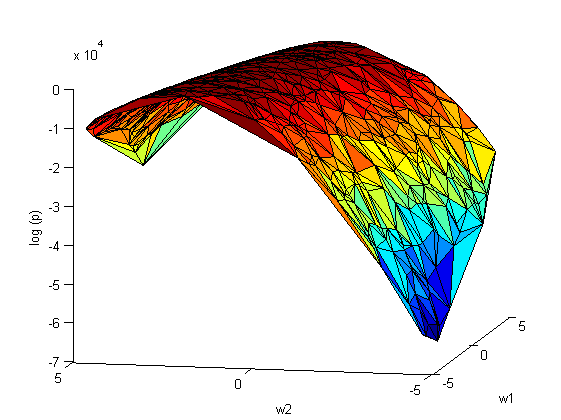
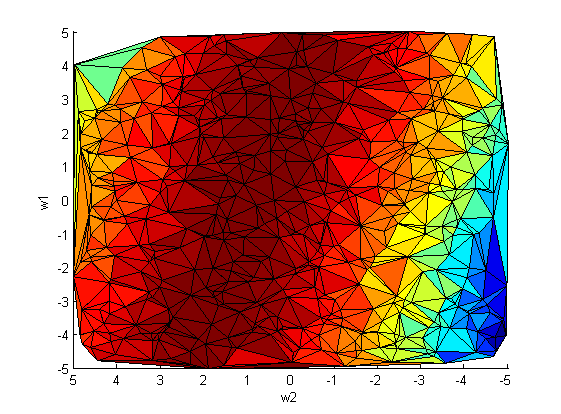
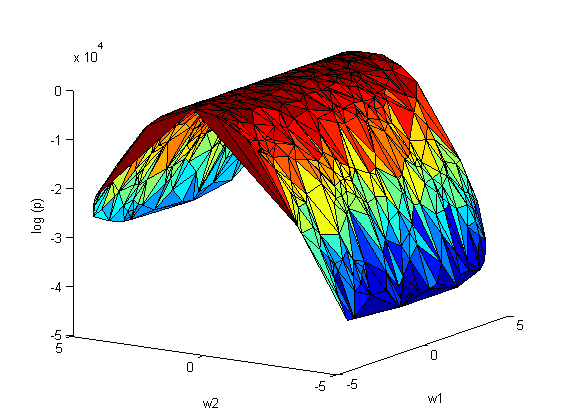
Повторим эксперимент, только теперь варируем сразу оба параметра $w_1$ и $w_2$ :

Рис. 1. Зависимость $- SSE$ от $w_1$ и $w_2$

Рис. 2. Зависимость от и . Ось log(p) направлена вверх

Рис. 2. Зависимость $- SSE$ от $w_1$ и $w_2$ . Ось log(p) направлена вверх

апроксимация Лапласса:

Laplace approximation

$D_{kl}(p_{SSE},p_{lap})=1.2481$

На рис.2 наблюдается зависимость между коэффициентами $w_1$ и $w_2$ . Следовательно, ковариационная матрица $cov(w_1,w_2)$ не будет диагональной.

Смотри также

Литература

Bishop, C. Pattern Recognition And Machine Learning. Springer. 2006.

Примечания

Данная статья является непроверенным учебным заданием.

Студент: Евгений Зайцев

Преподаватель: В.В.Стрижов

Срок: 24 декабря 2010

До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru. По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}.

См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.

Источник — «http://www.machinelearning.ru/wiki/index.php?title=%D0%90%D0%BF%D0%BF%D1%80%D0%BE%D0%BA%D1%81%D0%B8%D0%BC%D0%B0%D1%86%D0%B8%D1%8F_%D0%9B%D0%B0%D0%BF%D0%BB%D0%B0%D1%81%D0%B0_%28%D0%BF%D1%80%D0%B8%D0%BC%D0%B5%D1%80%29»

Категории: Непроверенные учебные задания | Практика и вычислительные эксперименты

@@ Строка 17: / Строка 17: @@
 Задана выборка — множество <tex>X^N=\{{x}_1,\ldots,{x}_N|x\in\R^M\}</tex> значений свободных переменных и множество <tex>\{y_1,\ldots, y_N| y\in\R\}</tex> соответствующих им значений зависимой переменной.
-Необходимо для выбранной регрессионной модели <tex>f(\mathbf{w},\mathbf{x})</tex>
+Необходимо для выбранной регрессионной модели <tex>f(\mathbf{w},\mathbf{x})</tex>:
 # показать зависимость среднеквадратичной ошибки от значений параметров модели: <tex>SSE=SSE(w)</tex>;
 # построить график и сделать апроксимацию Лапласа для нее;