Метод потенциальных функций
Материал из MachineLearning.
м (→Выбор параметров) |
(дополнение, формулы, ссылки, стилевые правки) |
||
| Строка 1: | Строка 1: | ||
| - | + | '''Метод потенциальных функций''' - [[метрический классификатор]], частный случай [[Метод ближайших соседей|метода ближайших соседей]]. Позволяет с помощью простого алгоритма оценивать вес («важность») объектов [[Выборка|обучающей выборки]] при решении задачи [[классификация|классификации]]. | |
| - | '''Метод потенциальных функций''' - [[метрический классификатор]], частный случай [[Метод ближайших соседей|метода ближайших соседей]]. Позволяет с помощью простого алгоритма оценивать вес («важность») объектов [[Выборка|обучающей выборки]] при решении задачи классификации. | + | |
| - | == | + | == Постановка задачи классификации == |
| - | + | Приведём краткую [[задача классификации|постановку задачи классификации]] в общем виде. | |
| + | Пусть имеется пространство объектов <tex>X</tex> и конечное множество классов <tex>Y</tex>. На множестве <tex>X</tex> задана функция расстояния <tex>\rho: X \times X \to [0, + \infty]</tex>. Каждый объект из <tex>X</tex> относится к некоторому классу из <tex>Y</tex> посредством отображения <tex>y^*:~X \to Y, </tex>. | ||
| + | Пусть также задана [[обучающая выборка]] пар «объект—ответ»: | ||
| + | <tex>X^m = \{(x_1,y_1),\dots,(x_m,y_m)\} \subseteq X \times Y</tex>. | ||
| + | Требуется построить [[алгоритм]] <tex>a(u,X^l)</tex>, который по заданной выборке <tex>X^l</tex> [[аппроксимация|аппроксимирует]] отображение <tex>y^*(u)</tex>. | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | + | == Идея метода == | |
| + | |||
| + | Общая идея метода иллюстрируется на примере электростатического взаимодействия элементарных частиц. Известно, что потенциал («мера воздействия») электрического поля элементарной заряженной частицы в некоторой точке пространства пропорционален отношению ''заряда'' частицы (Q) к расстоянию до частицы (r): <tex>\varphi(r) \sim \frac{Q}{r}</tex>. | ||
| + | |||
| + | Метод потенциальных функций реализует полную аналогию указанного выше примера. При классификации объект проверяется на близость к объектам из обучающей выборки. Считается, что объекты из [[выборка|обучающей выборки]] «заряжены» своим классом, а мера «важности» каждого из них при [[классификация|классификации]] зависит от его «заряда» и расстояния до классифицируемого объекта. | ||
| + | |||
| + | |||
| + | == Основная формула == | ||
Перенумеруем объекты обучающей выборки <tex>x_i \in X^l</tex> относительно удаления от объекта <tex>u</tex> индексами <tex>x_u^{p}</tex> (<tex>p=\overline{1,l}</tex>) – то есть таким образом, что <tex>\rho(u,x_u^{(1)}) \leq \rho(u,x_u^{(2)}) \leq \dots \leq \rho(u,x_u^{(l)})</tex>. | Перенумеруем объекты обучающей выборки <tex>x_i \in X^l</tex> относительно удаления от объекта <tex>u</tex> индексами <tex>x_u^{p}</tex> (<tex>p=\overline{1,l}</tex>) – то есть таким образом, что <tex>\rho(u,x_u^{(1)}) \leq \rho(u,x_u^{(2)}) \leq \dots \leq \rho(u,x_u^{(l)})</tex>. | ||
| Строка 25: | Строка 31: | ||
:: <tex>w(i,u)=\gamma(x_u^{(i)}) K \left(\frac{\rho(u,x_u{(i)})}{h(x_u{(i)})}\right)</tex>, где | :: <tex>w(i,u)=\gamma(x_u^{(i)}) K \left(\frac{\rho(u,x_u{(i)})}{h(x_u{(i)})}\right)</tex>, где | ||
| - | * <tex>K(r) = \frac{1}{r+a}</tex>. Константа <tex>a</tex> нужна чтобы избежать проблем с делением на ноль. Для простоты обычно полагают <tex>a=1</tex>. | + | * <tex>K(r) = \frac{1}{r+a}</tex> – функция, убывающая с ростом аргумента. Константа <tex>a</tex> нужна чтобы избежать проблем с делением на ноль. Для простоты обычно полагают <tex>a=1</tex>. |
* <tex>\rho(u,x_u{(i)})</tex> – расстояние от объекта u до i-того ближайшего к u объекта – <tex>x_u^{(i)}</tex>. | * <tex>\rho(u,x_u{(i)})</tex> – расстояние от объекта u до i-того ближайшего к u объекта – <tex>x_u^{(i)}</tex>. | ||
| - | * <tex> | + | * <tex>h(x_u{(i)})</tex> – параметр. Общий смысл – «ширина потенциала» объекта <tex>x_i \in X^l</tex>, <tex>\left(i=\overline{1,l}\right)</tex>. Вводится по аналогии с шириной окна в [[Метод парзеновского окна|методе парзеновского окна]]. |
| - | * <tex> | + | * <tex>\gamma(x_u^{(i)})</tex> – параметр. Общий смысл – «заряд» или степень «важности» объекта <tex>x_i \in X^l</tex>, <tex>\left(i=\overline{1,l}\right)</tex> при классификации; |
== Выбор параметров == | == Выбор параметров == | ||
| - | Как мы уже заметили, в основной формуле метода потенциальных функций используются две группы параметров: <tex>\{ | + | Как мы уже заметили, в основной формуле метода потенциальных функций используются две группы параметров: <tex>\{h(x_i)\}</tex> и <tex>\{\gamma(x_i)\}</tex>. |
| - | Ниже приведён алгоритм, который позволяет «обучать» параметры <tex>(\gamma(x_1), \dots, \gamma(x_n))</tex>, то есть подбирать их значения по обучающей выборке <tex>X^l</tex>. | + | «Ширина окна потенциала» <tex>h(x_i)</tex> выбирается для каждого объекта из эмпирических соображений. |
| + | |||
| + | «Важность» <tex>\gamma(x_i)</tex> объектов выборки можно подобрать, исходя из информации, содержащейся в выборке. Ниже приведён алгоритм, который позволяет «обучать» параметры <tex>(\gamma(x_1), \dots, \gamma(x_n))</tex>, то есть подбирать их значения по обучающей выборке <tex>X^l</tex>. | ||
Вход: Обучающая выборка из <tex>l</tex> пар «объект-ответ» – <tex>X^l=\left((x_1,y_1), \dots, (x_l,y_l) \right)</tex>. <br /> | Вход: Обучающая выборка из <tex>l</tex> пар «объект-ответ» – <tex>X^l=\left((x_1,y_1), \dots, (x_l,y_l) \right)</tex>. <br /> | ||
| Строка 61: | Строка 69: | ||
* Параметры <tex>\{\gamma_i\}</tex> и <tex>\{h_i\}</tex> настраиваются слишком грубо; | * Параметры <tex>\{\gamma_i\}</tex> и <tex>\{h_i\}</tex> настраиваются слишком грубо; | ||
* Значения параметров <tex>(\gamma_1,\dots,\gamma_l)</tex> зависят от порядка выбора объектов из выборки <tex>X^l</tex>. | * Значения параметров <tex>(\gamma_1,\dots,\gamma_l)</tex> зависят от порядка выбора объектов из выборки <tex>X^l</tex>. | ||
| + | |||
| + | == Замечания == | ||
| + | |||
| + | Полученные в результате работы алгоритма значения параметров <tex>(\gamma_1,\dots,\gamma_l)</tex> позволяют выделить из обучающей выборки подмножество [[эталон|эталонов]] – наиболее значимых с точки зрения классификации объектов. Как нетрудно видеть, теоретически на роль эталона подходит любой объект <tex>x_i</tex> с ненулевой «значимостью» <tex>\left(\gamma_i>0 \right)</tex>. | ||
| + | |||
| + | == См. также == | ||
| + | |||
| + | * [[Классификация]] | ||
| + | * [[Метрический классификатор]] | ||
| + | * [[Метод ближайших соседей]] | ||
| + | * [[Метод парзеновского окна]] | ||
| + | |||
| + | {{Задание|osa|Константин Воронцов|25 января 2010}} | ||
Версия 00:50, 5 января 2010
Метод потенциальных функций - метрический классификатор, частный случай метода ближайших соседей. Позволяет с помощью простого алгоритма оценивать вес («важность») объектов обучающей выборки при решении задачи классификации.
Содержание |
Постановка задачи классификации
Приведём краткую постановку задачи классификации в общем виде.
Пусть имеется пространство объектов и конечное множество классов
. На множестве
задана функция расстояния
. Каждый объект из
относится к некоторому классу из
посредством отображения
.
Пусть также задана обучающая выборка пар «объект—ответ»:
.
Требуется построить алгоритм , который по заданной выборке
аппроксимирует отображение
.
Идея метода
Общая идея метода иллюстрируется на примере электростатического взаимодействия элементарных частиц. Известно, что потенциал («мера воздействия») электрического поля элементарной заряженной частицы в некоторой точке пространства пропорционален отношению заряда частицы (Q) к расстоянию до частицы (r): .
Метод потенциальных функций реализует полную аналогию указанного выше примера. При классификации объект проверяется на близость к объектам из обучающей выборки. Считается, что объекты из обучающей выборки «заряжены» своим классом, а мера «важности» каждого из них при классификации зависит от его «заряда» и расстояния до классифицируемого объекта.
Основная формула
Перенумеруем объекты обучающей выборки относительно удаления от объекта
индексами
(
) – то есть таким образом, что
.
В общем виде, алгоритм ближайших соседей есть:
, где
– мера «важности» (вес) объекта
из обучающей выборки относительно классифицируемого объекта
.
Метод потенциальных функций заключается в выборе в качестве весовой функции следующего вида:
-
, где
-
-
– функция, убывающая с ростом аргумента. Константа
нужна чтобы избежать проблем с делением на ноль. Для простоты обычно полагают
.
-
– расстояние от объекта u до i-того ближайшего к u объекта –
.
-
– параметр. Общий смысл – «ширина потенциала» объекта
,
. Вводится по аналогии с шириной окна в методе парзеновского окна.
-
– параметр. Общий смысл – «заряд» или степень «важности» объекта
,
при классификации;
Выбор параметров
Как мы уже заметили, в основной формуле метода потенциальных функций используются две группы параметров: и
.
«Ширина окна потенциала» выбирается для каждого объекта из эмпирических соображений.
«Важность» объектов выборки можно подобрать, исходя из информации, содержащейся в выборке. Ниже приведён алгоритм, который позволяет «обучать» параметры
, то есть подбирать их значения по обучающей выборке
.
Вход: Обучающая выборка изпар «объект-ответ» –
.
Выход: Значения параметровдля всех
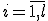
1. Начало. Инициализация:для всех
;
2. Повторять {
2.1 Выбрать очередной объектиз выборки
;
2.2 Если, то
;
3. } пока(то есть пока процесс не стабилизируется);
4. Вернуть значениядля всех
.
Преимущества и недостатки
Преимущества метода потенциальных функций:
- Метод прост для понимания и алгоритмической реализации;
- Порождает потоковый алгоритм;
- Хранит лишь часть выборки, следовательно, экономит память.
Недостатки метода:
- Порождаемый алгоритм медленно сходится;
- Параметры
и
настраиваются слишком грубо;
- Значения параметров
зависят от порядка выбора объектов из выборки
.
Замечания
Полученные в результате работы алгоритма значения параметров позволяют выделить из обучающей выборки подмножество эталонов – наиболее значимых с точки зрения классификации объектов. Как нетрудно видеть, теоретически на роль эталона подходит любой объект
с ненулевой «значимостью»
.
См. также
| | Данная статья является непроверенным учебным заданием.
До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru. По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}. См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе. |

