SVM для линейно неразделимой выборки (пример)

Материал из MachineLearning.

(Различия между версиями)

Версия 12:37, 28 апреля 2010

SVM (Support Vector Machine, машина опорных векторов) — алгоритм машинного обучения, предложенный В. Н. Вапником. Парадигмой машины опорных векторов можно считать выбор наиболее близких к границе классов объектов из обучающего набора, «опорных векторов», по которым и строится опорная гиперплоскость.

Изначально алгоритм позволял строить линейный классификатор с помощью минимизации ширины полосы раздела классов. Позднее были предложены методы обобщения алгоритма на случай линейно неразделимой выборки (например, введения штрафа за ошибки в функционал качества).

В данной статье приведен пример решения этой задачи для линейно неразделимой выборки с использованием функции ядра (в англоязычной литературе приём носит название kernel trick).

Содержание

1 Постановка задачи линейной классификации
2 Описание алгоритма
3 Вычислительный эксперимент
- 3.1 Нормальные распределения
- 3.2 Ирисы Фишера
4 Исходный код
5 Смотри также
6 Литература

Постановка задачи линейной классификации

Основная статья: Линейный классификатор

Задана выборка $X=\{(x_i,y_i)\}_{i=1}^l$ , где $x_i$ -признаковое описание i-го объекта, $y_i$ - идентификатор класса, которому принадлежит i-ый объект. В случае двух классов считаем, что $y_i\in\{-1,1\}$ (это позволяет пользоваться функцией sgn в описании классификатора).

Требуется построить классификатор вида $a(x)=sign(<w,x>-w_0)$ , где $<w,x>$ - скалярное произведение, а $w,w_0$ - вектор и число, характеризующий данный классификатор. Можно говорить о том, что $w_i$ -веса признаков, $w_0$ - порог принятия решения.

Если для данной выборки существуют $w,w_0$ такие, что $a(x)$ не ошибается на обучающей выборке, то она называется линейно разделимой. В противном случае, выборка называется линейно неразделимой.

Описание алгоритма

Линейно разделимая выборка

Если выборка линейно разделима, то существует бесконечно много линейных классификаторов, не ошибающихся на ней. В алгоритме SVM максимизируется расстояние от опорной гиперплоскости до обоих классов.

Отнормируем вектор нормали к разделяющей гиперплоскости $w$ и порог принятия решения $w_0$ так, чтобы выполнялось условие $\min\limits_{i=1,l} y_i(<w,x_i>-w_0)=1$ . Это всегда можно сделать, поскольку, во-первых, умножение $w,w_0$ на положительную константу не меняет классификатора, а, во-вторых, требование минимального расстояния от гиперплоскости до классов гарантирует нам, что плоскость находится на равном расстоянии от классов.

Нетрудно показать, что при такой нормировке ширина разделяющей полосы может быть представлена в виде: $\frac{2}{||w||}$ . Максимизация этой величины равносильна минимизации нормы вектора нормали. Таким образом, параметры линейного классификатора определяются из задачи квадратичного программирования: $\left{<w,w>\rightarrow min\\y_i(<w,x_i>-w_0)\ge1,\qquad i=1,...,l\\ \right.$

Линейно неразделимая выборка

Для линейно неразделимой выборки данная оптимизационная задача не будет иметь решения. Не отказываясь от принципа максимальности зазора, можно видоизменить задачу следующим образом. Разрешим существование неправильно классифицированных объектов, но за каждвый такой объект будем штрафовать:

$\left{\frac{1}{2}<w,w>+C\sum\limits_{i=1}^l\xi_i\rightarrow min\\y_i(<w,x_i>-w_0)\ge1-\xi_i,\qquad i=1,...,l\\ \xi_i\ge0,\qquad i=1,...,l\right.$

Используя аппарат функций Лагранжа, переходя к двойственной задаче, можно показать эквивалентность этой задачи и следующей.

(1)

$\left{-\sum\limits_{i=1}^l\lambda_i+\frac{1}{2}\sum\limits_{i=1}^l\sum\limits_{j=1}^l\lambda_i\lambda_jy_iy_j<x_i,x_j>\rightarrow \min\limits_\lambda \\ 0\le\lambda_i\le C\quad i=1,...,l\\ \sum\limits_{i=1}^l\lambda_iy_i=0\quad i=1,...,l\right.$

При этом выполняются соотношения $w = \sum\limits_{i=1}^l\lambda_ix_iy_i,\qquad\eta_i+\lambda_i=C,\qquad \lambda_i(1-\xi_i)=0, \qquad \xi_i\eta_i=0 \forall i:1,...,l$ .

Решив эту оптимизационную задачу, то есть, найдя вектор $\lambda$ , классифицируем i-ый объект следующим образом:

$\lambda_i=0, \eta_i=C, \xi_i=0.$

В этом случае объект $x_i$ классифицировался правильно(т.к. $\xi_i=0$ ). Но, что важнее, вектор опорной гиперплоскости не зависит от данного объекта. Его можно исключить из выборки, и алгоритм SVM построит ту же самую разделяющую гиперплоскость. Такие объекты называются периферийными.

$0<\lambda_i<C, 0<\eta_i<C, \xi_i=0.$

Объект $x_i$ классифицируется правильно и лежит точно на границе разделяющей полосы. Данные объекты называются опорными граничными.

$\lambda_i=C, \eta_i=0, \xi_i>0.$

Данный объект может находить как в граничной полосе со стороны своего класса, так и классифицироваться неправильно. Данные объекты называются опорными нарушителями.

Объекты последних двух типов и называются опорными векторами. Разделяющая гиперплоскость зависит только от них, что является одним из главных преимуществ SVM. Можно ожидать, что этих векторов будет не очень много, и оставит только их в памяти, алгоритм классификации ничуть не изменится.

Заметим, что на практике оптимизационная задача решается не абсолютно точно. В следствии чего периферийные объекты (представляющие собой вырожденный случай распределения параметров) почти не встречаются. Для каждого объекта вычисляется $\lambda_i$ не равное нулю, но для большинства объектов их значение мало "в среднем". Поэтому не составляет труда отсеять периферийные объекты.

Важно отметить также, что решение двойственной задачи квадратичного программирования единственно, т.к. функционал является выпуклым и множество ограничений является выпуклым.

Таким образом, решив задачу (1), вычислим $w = \sum\limits_{i=1}^l\lambda_ix_iy_i, \qquad w_0=med\{<w_i,x_i>-y_i|\lambda_i>0,\xi_i=0, i=1,...,l\}$ . Медиана здесь вычисляется именно из практических соображений неточного решения оптимизационной задачи. Теоретически все значения в множестве, по которому берется среднее, равны. Параметры разделяющей гиперплоскости построены.

Спрямляющее пространство и функции ядра

Описание объекта никогда не может считаться полным, если мы работаем с задачами реального мира. Перейдём к новому описанию выборки, основываясь на её данном признаковом представлении, и в этом новом описании будем вычислять скалярное произведение. В новом пространстве (называемом спрямляющим пространством), если оно большей размерности, выборка может оказаться линейно разделимой. Вычисление разделяющей гиперплоскости в спрямляющем пространстве может привести к удовлетворительному результату в исходном представлении. Однако, этого никто гарантировать не может, и более того, выбор ядра для данной практической задачи является нерешенной теоретической проблемой.

Приведенные рассуждения можно записать формальным образом.

$\psi:X\rightarrow H$ , где X - исходное пространство, а H - гильбертово пространство. Описание $x_i$ заменяется описанием $\psi(x_i)$ . Тогда скалярное произведение $<x_i,x_j>_X$ заменяется новым скалярным произведением $<\psi(x_i),\psi(x_j)>_H$ .

Однако заметим, что параметры задачи (1) (которую мы и хотим решить) зависят только от попарных скалярных произведений описаний объектов выборки. Это означает, что,в принципе, нам не требуется знать новые описания объектов, а только вычислять скалярное произведение между ними. Естественным образом введём следующее определение.

Функция $K(x,y):X\times X\rightarrow \mathbb{R}$ называется ядром, если существует такое преобразование $\psi:X\rightarrow H$ и $K(x,y)=<\psi(x),\psi(y)>_H$ . В качестве ядра, конечно, подойдёт не любая функция, на вопрос о требованиях к ней отвечает

Теорема Мерсера

Функция двух переменных $K$x,x'$$ является ядром тогда и только тогда, когда она

симметрична, то есть $K$x,x'$ = K$x',x$$ ;
неотрицательно определена, то есть $\int_X\int_X K$x,x'$g$x$g$x'$dxdx' \geq 0$ .

В данном примере мы ограничились ядрами:

$K(x,y)=(<x,y>)^d$ , где d - натуральный параметр
$K(x,y)=(1+<x,y>)^d$ , где d - натуральный параметр
$K(x,y)=th(k_0+k_1<x,y>)$ , где $k_0,k_1$ - положительные параметры (однако, не совсем произвольные)

Данное ядро отвечает классической нейронной сети с сигмоидными функциями активации.

$K(x,y)=\e^{(-\gamma||x-y||^2)}$ , где $\gamma>0$

Данное ядро отвечает нейронной сети с радиальными базисными функциями.

Вычислительный эксперимент

Работа алгоритма изучалась на двух выборках: сгенерированной вручную и канонической выборкой ирисов.

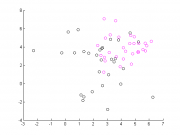
Нормальные распределения

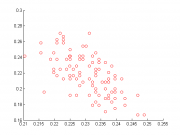
Справа на рисунке приведена сгенерированная выборка, состоящая из двух классов по 30 объектов в каждом.

Алгоритм запускался на данной выборке с разными ядрами, используя процедуру скользящего контроля. Для каждого из типов ядер, описанных выше, для набора значений параметров изучалось количество ошибок на обучающей выборке и на контрольной. Приведенные результаты изображены на графике, где одним цветом обозначены ядра одного типа, но с разными параметрами. По оси абсцисс - процент ошибок на обучающей выборке, по оси ординат - на контрольной.

Справа приведен увеличенный участок этого изображения, на котором отмечены только точки, отвечающие ядру с сигмоидальной активацией.

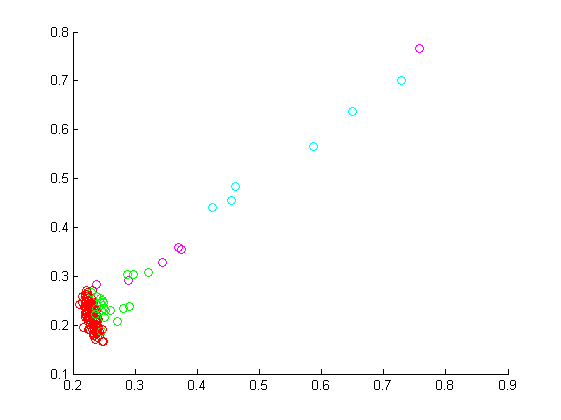
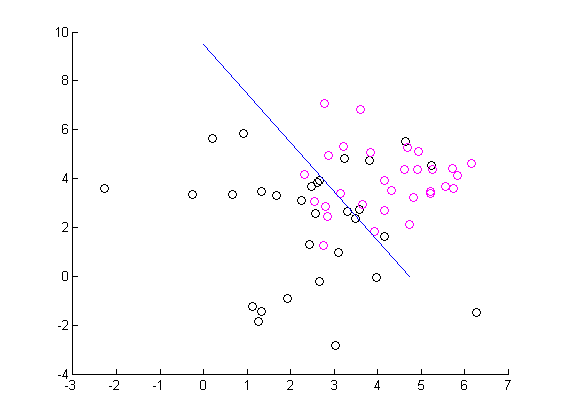
Очевидно, выделяется точка, находящаяся ближе всех к началу координат. Разделяющая прямая, построенная с помощью этого ядра изображена ниже.

Ирисы Фишера

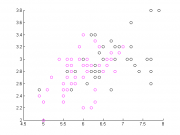
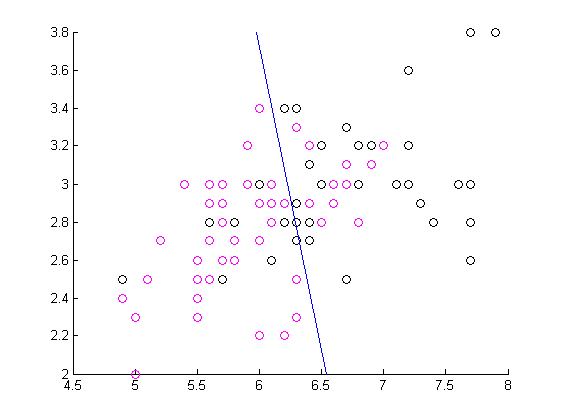
Ирисы Фишера являются одним из наиболее популярных примеров данных для задачи классификации. Это связано, в первую очередь, с тем, что количество признаков всего 5 и все они численные, а классов всего лишь 3. При этом два из классов линейно отделимы от третьего, но линейно неразделимы между собой. В данном примере для наглядности изображения данных на плоскости были взяты только два признака двух линейно неразделимых классов ирисов. Ниже приведена обучающая выборка.

Алгоритм запускался по той же схеме, что и для синтетических данных. Результаты приведены на следующем графике:

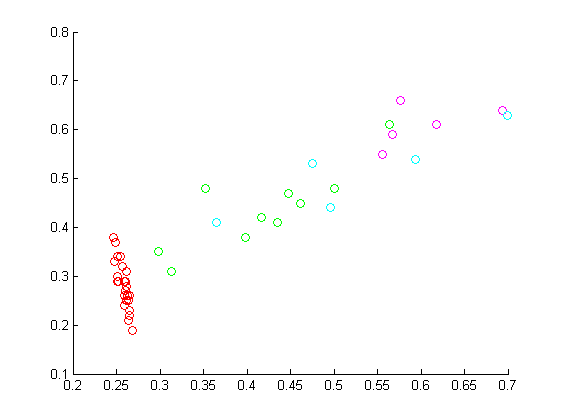
Было выбрано ядро, находящееся ближе всего к нулю на данном графике (в смысле евклидового расстояния). Алгоритм с данным ядром строит для ирисов Фишера следующую разделающую гиперплоскость:

Исходный код

Код MATLAB можно скачать здесь: [1]

Смотри также

Литература

Воронцов К.В. Лекции по линейным алгоритмам классификации
Вапник В.Н., Червоненкис А.Я. Теория распознавания образов. Статистические проблемы обучения. - Москва, "Наука", 1974.
Cortes C., Vapnik V. Support Vector Networks.

Данная статья является непроверенным учебным заданием.

Студент: Участник:Павел Сечин

Преподаватель: Участник:В.В.Стрижов

Срок: 28 мая 2010

До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru. По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}.

См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.

Источник — «http://www.machinelearning.ru/wiki/index.php?title=SVM_%D0%B4%D0%BB%D1%8F_%D0%BB%D0%B8%D0%BD%D0%B5%D0%B9%D0%BD%D0%BE_%D0%BD%D0%B5%D1%80%D0%B0%D0%B7%D0%B4%D0%B5%D0%BB%D0%B8%D0%BC%D0%BE%D0%B9_%D0%B2%D1%8B%D0%B1%D0%BE%D1%80%D0%BA%D0%B8_%28%D0%BF%D1%80%D0%B8%D0%BC%D0%B5%D1%80%29»

Категории: Непроверенные учебные задания | Учебные материалы | Классификация | Линейные классификаторы

@@ Строка 103: / Строка 103: @@
 == Исходный код ==
+Код MATLAB можно скачать здесь: [https://mlalgorithms.svn.sourceforge.net/svnroot/mlalgorithms/SVM_nonlinear/]
 == Смотри также ==
 * [[ Машина опорных векторов ]]