SVM регрессия (пример)

Материал из MachineLearning.

(Различия между версиями)

Версия 00:08, 29 апреля 2010

SVM (Support Vector Machine, машина опорных векторов) — это особый класс алгоритмов, который характеризуется использованием ядер, отсутствием локальных минимумов, и используется для решения задач классификации и регрессии. В этой статье рассматривается пример использования метода опорных векторов в задачах регрессии.

Постановка задачи

Дано: Обучающая выборка $X=\{(x_i,y_i)\}_{i=1}^{\ell}$ , где $x_i$ -признаковое описание i-го объекта, $y_i$ - характеристика, приписываемая объекту. Функция потерь имеет вид $a(x_i)=\mid (w,f(x_i))-w_0-y_i \mid_\epsilon$ для каждого вектора $(x_i,y_i)$ , где $\mid z \mid_\epsilon = max(0,\mid z \mid-\epsilon)$ .

Найти: такую функцию $f_0$ , которая описывает зависимость $E(y|\mathbf{x})=f_0(\mathbf{x})$ наилучшим образом.

Алгоритм

Основная статья: Машина опорных векторов

В этом примере решается задача построения линейной SVM регрессии. Для этого решается прямая задача минимизации функционала потерь, в предположении что решение задается линейной комбинацией неких порождающих функций, из которых можем составить вектор-функцию $f(x)=\begin{Vmatrix} f_1(x) \\ f_2(x) \\ \vdots \\ f_k(x) \end{Vmatrix}$ .

Тогда функционал примет вид:

$Q_\epsilon(a,X)=\sum_{i=1}^\ell \mid (w,f(x_i))-w_0-y_i \mid_\epsilon + \tau (w,w)^2 \rightarrow \underset{w,w_0}{min}$

В предположении что

$f_0(x)=\sum_{i=1}^k w_i f_i(x)$

Для этого вводятся обозначение $C=\frac{1}{2\tau}$ и дополнительные переменные $\xi_i^+$ и $\xi_i^-$ :

$\xi_i^+=(a(x_i)-y_i-\epsilon)_+$ , $\xi_i^-=(-a(x_i)+y_i-\epsilon)_-$ , $i=1,...,l$ .

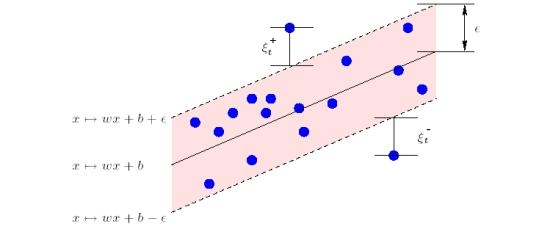
Геометрический смысл $\xi_i^+$ и $\xi_i^-$ :

Далее решается задача квадратичного программирования:

$\begin{cases} \frac{1}{2} (w,w)^2 + C\sum_{i=1}^\ell(\xi_i^+ + \xi_i^-)\rightarrow \underset{w,w_0,\xi_i^+,\xi_i^-}{min}, \\ (w,f(x_i))-w_0 \le y_i + \epsilon + \xi_i^+, & i=1,..,\ell; \\ (w,f(x_i))-w_0 \ge y_i - \epsilon - \xi_i^-, & i=1,..,\ell; \\ \xi_i^- \ge 0, \mbox{ } i=1,..,\ell; \\ \xi_i^+ \ge 0, \mbox{ } i=1,..,\ell; \\ \end{cases}$

Эту же задачу можно преобразовать к виду $\frac{1}{2}u^T H u + g u\rightarrow \underset{u}{min}$ , при условии, что $A u \le b,\$ а также, $lb \le u$ , где $u$ - вектор-столбец, составленный из столбцов $w\ , \xi_i^+, \xi_i^-$ , тоесть, где все переменные объеденены в один столбец неизвестных. В таких обозначениях $H=diag(1,1,...,1,0,0,...,0),\ g=(0,0,...,0,1,1,...,1)$ , где единиц и нулей в $H$ и $g$ соответственно столько же, сколько порождающих фукций, а размерность матрицы $H$ и вектора $g$ равна размерности $u$ .

Теперь построим матрицу А и столбцы $b$ и $lb$ . Преобразуем задачу квадратичного программирования к виду

$\begin{cases} \frac{1}{2} (w,w)^2 + C\sum_{i=1}^\ell(\xi_i^+ + \xi_i^-)\rightarrow \underset{w,w_0,\xi_i^+,\xi_i^-}{min}, \\ (w,f(x_i)) + w_0 -\xi_i^+ \le y_i + \epsilon , & i=1,..,\ell; \\ -(w,f(x_i))+ w_0 -\xi_i^- \le -y_i + \epsilon , & i=1,..,\ell; \\ 0 \le \xi_i^-, \mbox{ } i=1,..,\ell; \\ 0 \le \xi_i^+, \mbox{ } i=1,..,\ell; \\ \end{cases}$

Получаем, $A=\begin{Vmatrix} f^T(\x_1) & -1 & 0 & \cdots & 0 \\ f^T(\x_2) & 0 & -1 & \cdots & 0 \\ \vdots & \vdots &\vdots & \ddots & \vdots \\ f^T(\x_\ell) & 0 & 0 & \vdots & 0 \\ -f^T(\x_1) & 0 & 0 & \vdots & 0 \\ \vdots & \vdots &\vdots & \ddots & \vdots \\ -f^T(\x_\ell) & 0 & 0 & \cdots & -1 \\ \end{Vmatrix},\ b= \begin{Vmatrix} y_1 + \epsilon \\ y_2 + \epsilon \\ \vdots \\ y_\ell + \epsilon \\ -y_1 + \epsilon \\ \vdots \\ -y_\ell + \epsilon \\ \end{Vmatrix},\ lb= \begin{Vmatrix} -\infty \\ -\infty \\ \vdots \\ -\infty \\ 0 \\ \vdots \\ 0 \\ \end{Vmatrix}$ , и количество минус бесконечностей в lb равно количеству порождающих функций, а количество нулей равно $2\ell$ .

Таким образом, мы свели задачу к задаче квадратичного программирования.

В нашем примере значения С, $\epsilon$ и порождающие функции задаются экспертом.

Вычислительный эксперимент

Вычислительный эксеримент состоит из трех основных частей:

Генерация данных;
Работа алгоритма;
Визуализация и анализ данных.

Генерация данных

При генерации данных мы выбираем некую линейную комбинацию наших порождающих функций, и добаляем к ней случайный шум. В ходе эксперимента исследуются различные, как дискретные, так и непрерывные шумы.

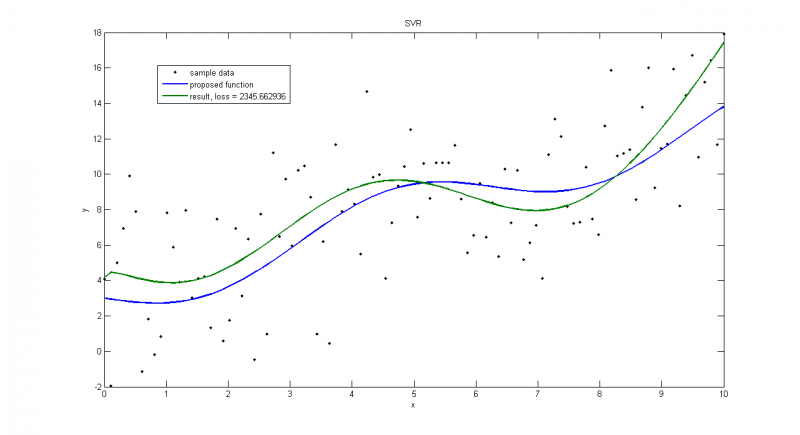
Нормальное распределение

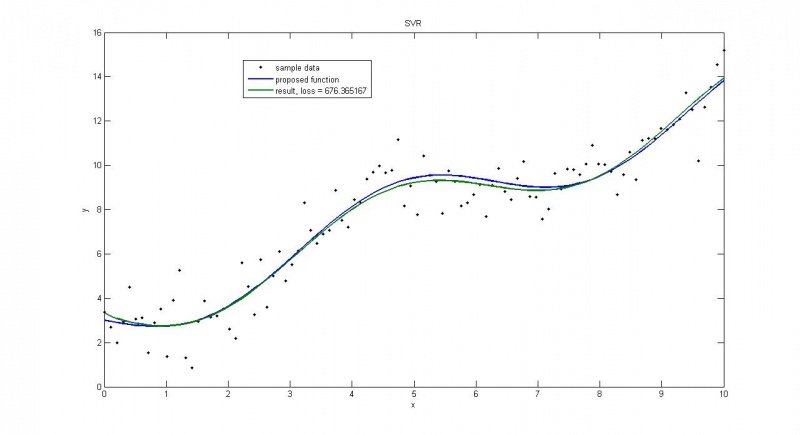
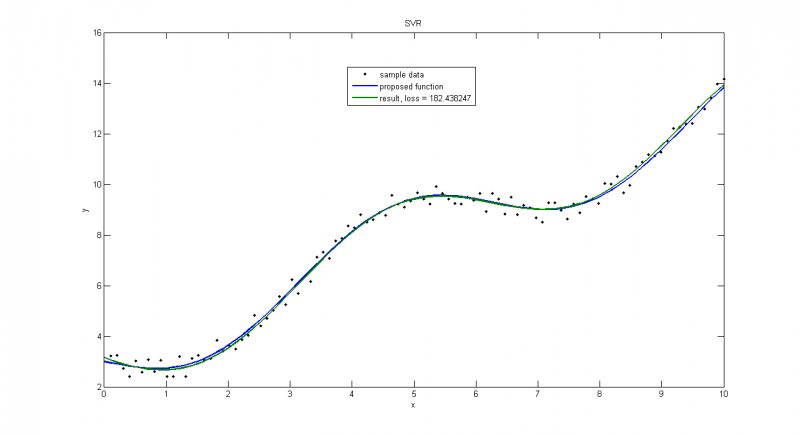
$\Uparrow$ дисперсия=1

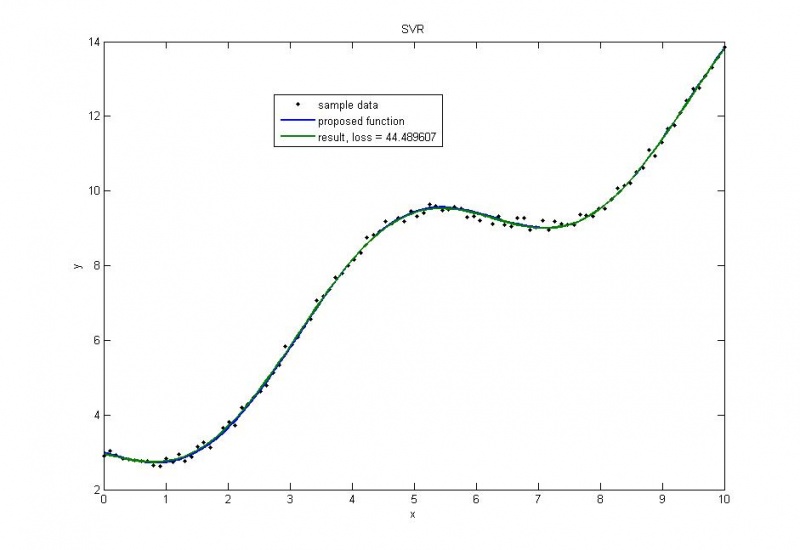
$\Uparrow$ дисперсия=0.1

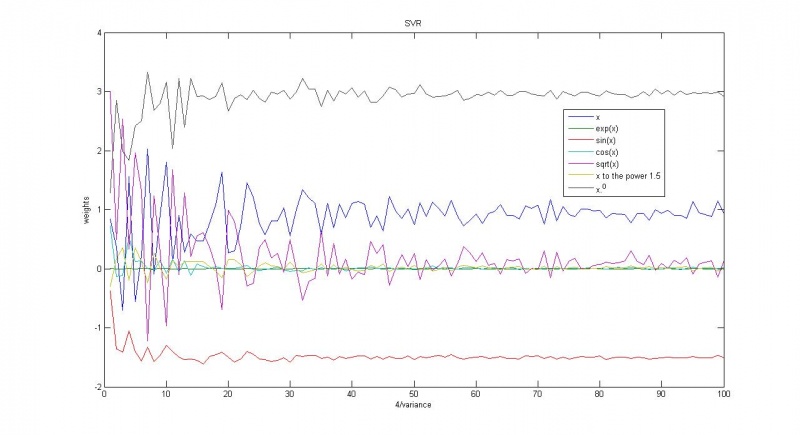
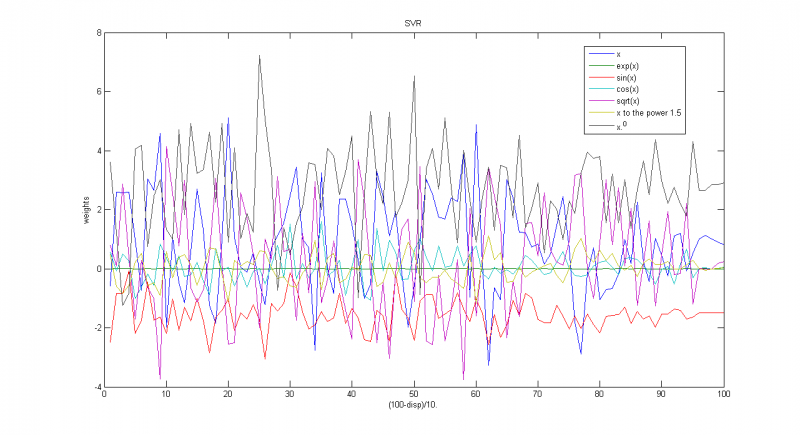
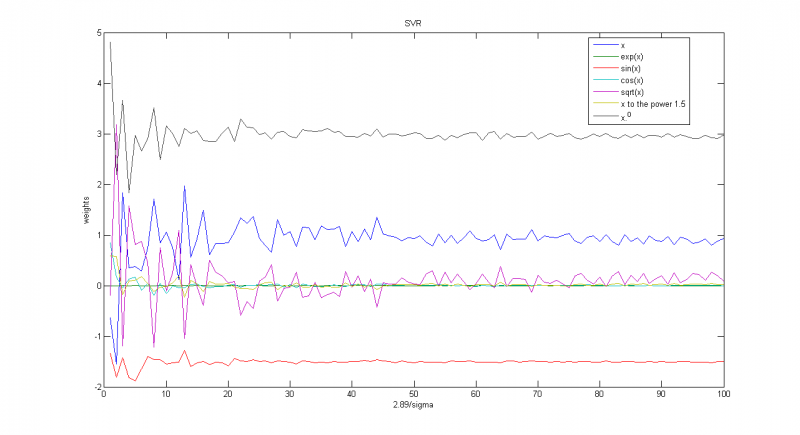
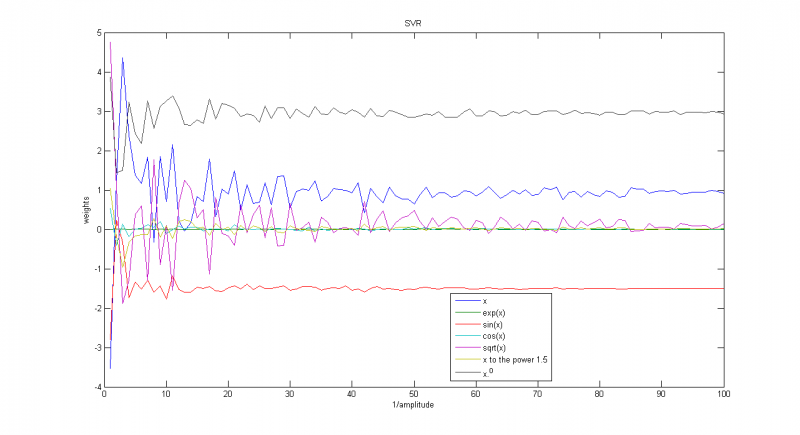
$\Uparrow$ Зависимость весов соответствующих функций от обратной дисперсии

Пуассоновское распределение

$\Uparrow$ Пуассоновское распределение с большой дисперсией

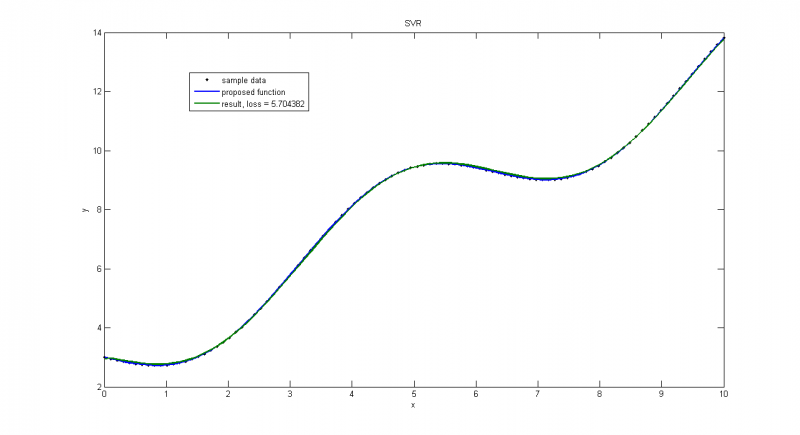
$\Uparrow$ Пуассоновское распределение с малой дисперсией, получаем почти точное решение

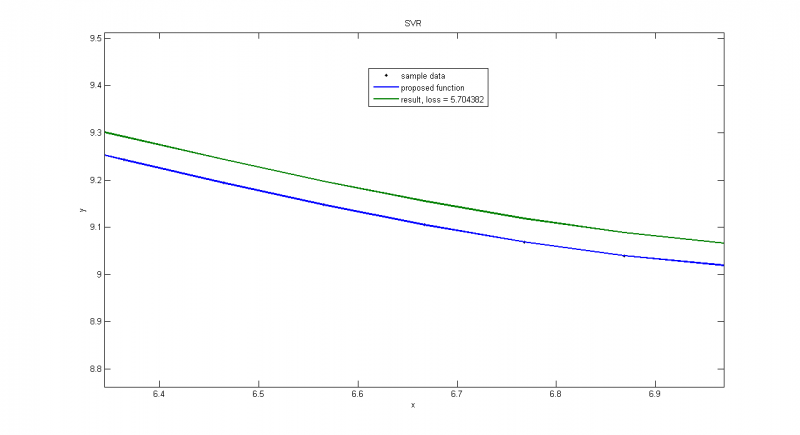
$\Uparrow$ Часть предыдущего графика, на которой мы видим, что даже с иделаьными данными мы не получим идеальное приближение, т.к. среди прочего минимизируем $(w,w)$

$\Uparrow$ Зависимость весов соответствующих функций от параметра

Равномерное распределение

$\Uparrow$ Работа алгоритма на примере с равномерным шумом. На этом графике шум равномерно распределен на отрезке $[-\frac{1}{2};\\frac{1}{2}]$

$\Uparrow$ Зависимость весов соответствующих функций от параметра

Распределение sin(unif)

Тест на распределении вида sin(unifrnd(-3.1415/2,3.1415/2))/parameter, тоесть синуса от равномерного распределения.

$\Uparrow$ Если выбрать большую амплитуду(=5), решение может сильно отличаться от верного

$\Uparrow$ При малых(=0.5) такого не наблюдается.

$\Uparrow$ Зависимость весов соответствующих функций от параметра

Реальные данные

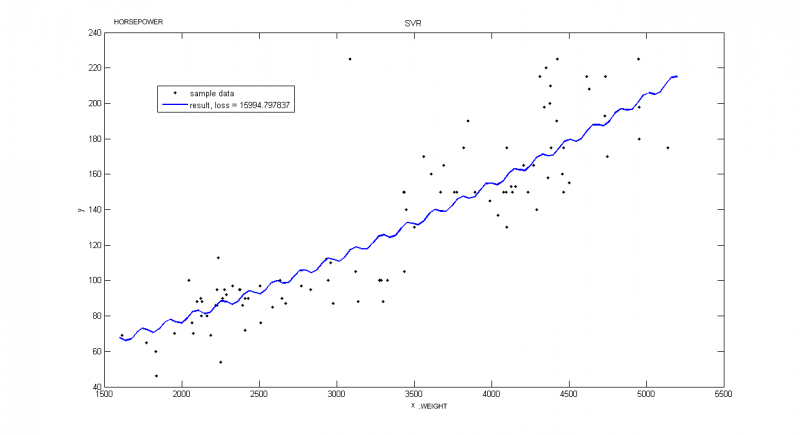
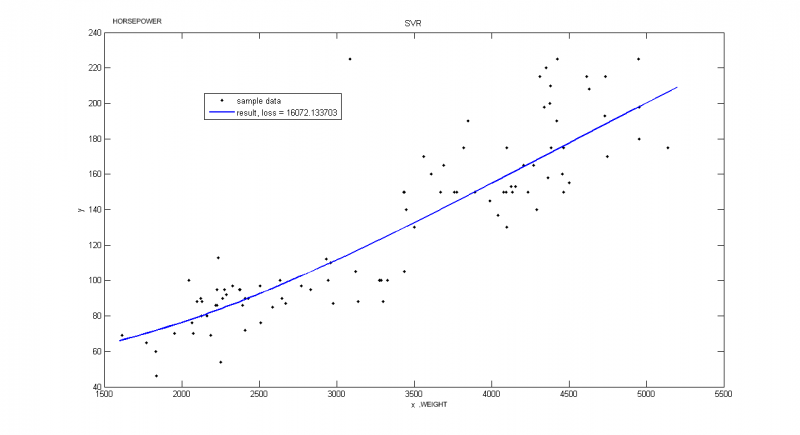
Пример взят из Репозитория UCI. В этом примере рассматриваются автомобили 1970-1973 года выпуска. Строится зависимость мощьности автомобиля [л.с.] от веса [кг]

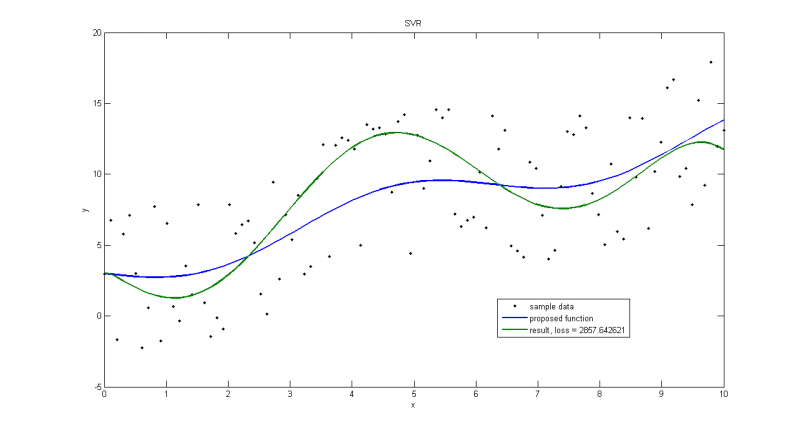
$\Uparrow$ Пример иллюстрирует, что очень важно правильно выбирать порождающие функции. Хотя потери меньше, чем на следующем графике, такое решение не является достаточно точным.

$\Uparrow$ Вектор порождающих функций: f = [x, exp(-x), sin(x), cos(x), sqrt(x), diag(x)*sqrt(x), x.^0];

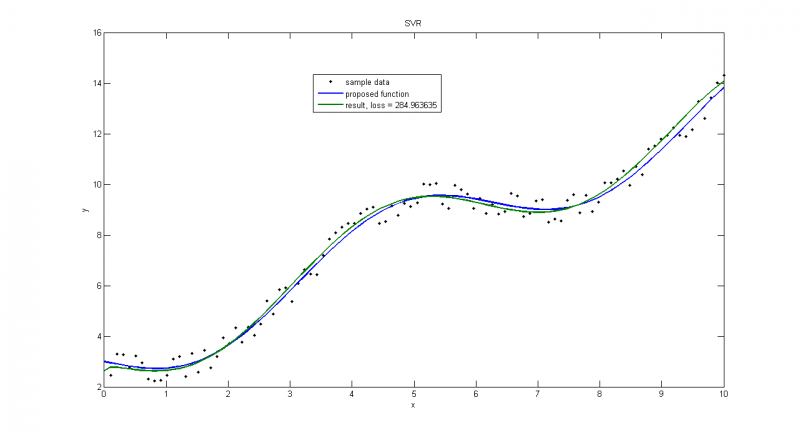
$\Uparrow$ Вектор порождающих функций: f = [x, exp(-x), diag(x)*(x), 0*cos(x), sqrt(x), diag(x)*sqrt(x), x.^0];

Исходный код

Смотри также

машина опорных векторов Википедия tripod.com

Литература

Alex J. Smola, Bernhard Schölkopf. A tutorial on support vector regression. DOI Bookmark: 10.1023/B:STCO.0000035301.49549.88

Данная статья является непроверенным учебным заданием.

Студент: Участник:Алексей Корниенко

Преподаватель: Участник:В.В.Стрижов

Срок: 28 мая 2010

До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru. По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}.

См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.

Источник — «http://www.machinelearning.ru/wiki/index.php?title=SVM_%D1%80%D0%B5%D0%B3%D1%80%D0%B5%D1%81%D1%81%D0%B8%D1%8F_%28%D0%BF%D1%80%D0%B8%D0%BC%D0%B5%D1%80%29»

Категории: Непроверенные учебные задания | Учебные материалы | Классификация | Линейные классификаторы

@@ Строка 172: / Строка 172: @@
 <tex>\Uparrow</tex>Вектор порождающих функций: f = [x, exp(-x), diag(x)*(x), 0*cos(x), sqrt(x), diag(x)*sqrt(x), x.^0];
+== Исходный код ==
+== Смотри также ==
+[[машина опорных векторов]]
+[http://en.wikipedia.org/wiki/Support_vector_machine#Regression Википедия]
+[http://kernelsvm.tripod.com/ tripod.com]
+== Литература ==
+*Alex J. Smola, Bernhard Schölkopf. A tutorial on support vector regression. DOI Bookmark: [http://dx.doi.org/10.1023/B:STCO.0000035301.49549.88 10.1023/B:STCO.0000035301.49549.88]
 {{Задание|Алексей Корниенко|В.В.Стрижов|28 мая 2010}}

SVM регрессия (пример)

Материал из MachineLearning.

Версия 00:08, 29 апреля 2010

Содержание

Постановка задачи

Алгоритм

Вычислительный эксперимент

Генерация данных

Нормальное распределение

Пуассоновское распределение

Равномерное распределение

Распределение sin(unif)

Реальные данные

Исходный код

Смотри также

Литература

Просмотры

Личные инструменты

Навигация

Поиск

Инструменты