Аппроксимация Лапласа (пример)

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск
(→Постановка задачи)
(→Описание алгоритма)
Строка 24: Строка 24:
<tex>Z_D</tex> - нормировачный коэффициент.
<tex>Z_D</tex> - нормировачный коэффициент.
-
'''3-1'''. В заданной модели ''f'', используя [[метод наименьших квадратов]], находим оптимальное значение вектора параметров <tex>\mathcal w_{opt}</tex>. Далее, фиксируем все параметры выбранной регрессионной модели (для определенности зададим им оптимальные значения) кроме одного (пусть этот незафиксированный параметр будет ''w(1)''). После чего, варируя значение ''w(1)'', строим искомую зависимость <tex>SSE=SSE(w(1))</tex> и его график. Таким образом построена зависимость от одного параметра ''w(1)''. Аналогично действуя, строится зависимость от большего количества параметров.
+
'''3-1'''. В заданной модели ''f'', используя [[метод наименьших квадратов]], находим оптимальное значение вектора параметров <tex>\mathcal w_{opt}</tex>. Далее, фиксируем все параметры выбранной регрессионной модели (для определенности зададим им оптимальные значения) кроме одного (пусть этот незафиксированный параметр будет <tex>w_1</tex>). После чего, варируя значение <tex>w_1</tex>, строим искомую зависимость <tex>SSE=SSE(w_1)</tex> и его график. Таким образом построена зависимость от одного параметра <tex>w_1</tex>. Аналогично действуя, строится зависимость от большего количества параметров.
'''3-2'''.
'''3-2'''.

Версия 01:08, 8 декабря 2010

Аппроксимация Лапласа - способ оценки параметров нормального распределения при апроксимации заданой плотности вероятности.


Содержание

Постановка задачи

Задана выборка — множество X^N=\{{x}_1,\ldots,{x}_N|x\in\R^M\} значений свободных переменных и множество \{y_1,\ldots, y_N| y\in\R\} соответствующих им значений зависимой переменной. Необходимо для выбранной регрессионной модели f(w,x):

3-1 показать зависимость среднеквадратичной ошибки от значений параметров модели: SSE=SSE(w);

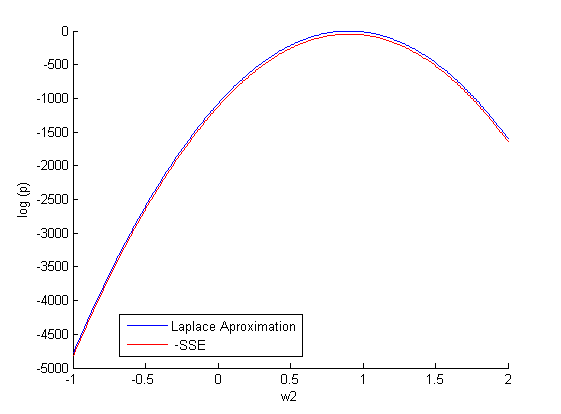
3-2 построить график и сделать апроксимацию Лапласа для зависимости SSE=SSE(w);

3-3 найти расстояния между получеными зависимостями, используя расстояние Кульбака - Лейблера.

Описание алгоритма

При востановлении регрессии рассматривалась следующая гипотеза порождения данных:

y=f(x,w)

В таком случае, при фиксированной модели f плотность вероятности появления данных равняется[1]:

p(y|x,w)=\frac{1}{Z_D}exp(-E_D), где

E_D - это функция регрессионных невязок, т.е. SSE;

Z_D - нормировачный коэффициент.

3-1. В заданной модели f, используя метод наименьших квадратов, находим оптимальное значение вектора параметров \mathcal w_{opt}. Далее, фиксируем все параметры выбранной регрессионной модели (для определенности зададим им оптимальные значения) кроме одного (пусть этот незафиксированный параметр будет w_1). После чего, варируя значение w_1, строим искомую зависимость SSE=SSE(w_1) и его график. Таким образом построена зависимость от одного параметра w_1. Аналогично действуя, строится зависимость от большего количества параметров.

3-2.

3-3. Расстояние Кульбака - Лейблера между двумя распределениями p(z) и q(z) равняется:

D_{kl}(p,q)=\sum\limits_{z\in \mathcal{Z}} p(z) \ln \frac{p(z)}{q(z)}

Вычислительный эксперимент

Обозначим плотность распределения SSE как p_{SSE}, а его апроксимация лапласса p_{lap}.


Во время вычислительного эксперимента SSE принимало достаточно большие значения (порядка 10^3 - 10^4). Как следствие, p(y) принимало значения порядка 1, и апроксимация Лапласса была некоректной.

Поэтому, апроксимация Лапласса применялась не к самому распределению p(y), а к ln(p(y)) (т.е. к -SSE c точностью до коэффициента).



Пример 1

Задуманная функция y=x + sin3x. Рассматривается линейная регрессионная модель с двумя параметрами: y(x)=w_1+w_2x. w_1_{opt} и w_2_{opt} - оптимальное значение параметров (при которых SSE минимально).

Фиксируем один параметр w_1=w_1_{opt} и задаем различные значение w_2 (500 случайных значений на отрезке [-1;2]). Строим зависимость:

D_{kl}(p_{SSE},p_{lap})=0.0085.

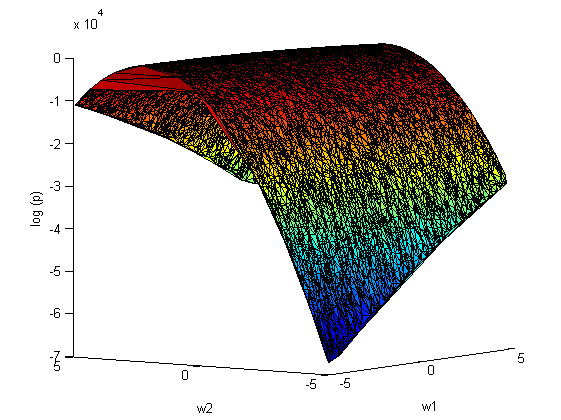
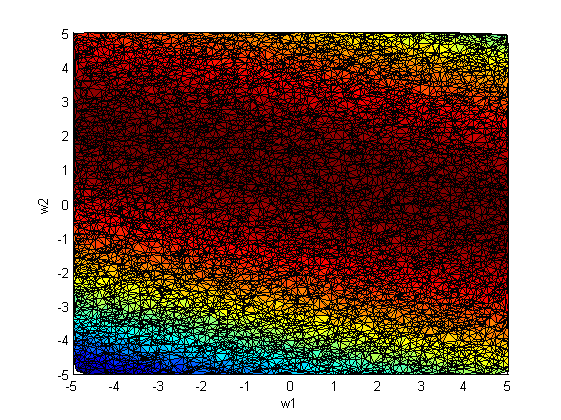
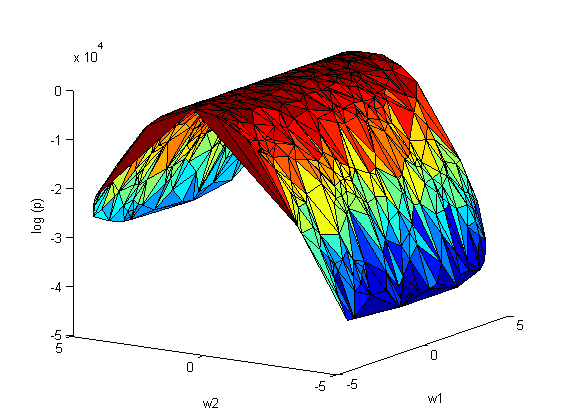
Повторим эксперимент, только теперь варируем сразу оба параметра w_1 и w_2:

Рис. 1. Зависимость от и
Рис. 1. Зависимость - SSE от w_1 и w_2
Рис. 2. Зависимость от и . Ось log(p) направлена вверх
Рис. 2. Зависимость - SSE от w_1 и w_2. Ось log(p) направлена вверх

апроксимация Лапласса:

Laplace approximation
Laplace approximation

D_{kl}(p_{SSE},p_{lap})=1.2481

На рис.2 наблюдается зависимость между коэффициентами w_1 и w_2. Следовательно, ковариационная матрица cov(w_1,w_2) не будет диагональной.

Смотри также

Литература

  • Bishop, C. Pattern Recognition And Machine Learning. Springer. 2006.

Примечания



Данная статья является непроверенным учебным заданием.
Студент: Евгений Зайцев
Преподаватель: В.В.Стрижов
Срок: 24 декабря 2010

До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru. По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}.

См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.

Источник — «http://www.machinelearning.ru/wiki/index.php?title=%D0%90%D0%BF%D0%BF%D1%80%D0%BE%D0%BA%D1%81%D0%B8%D0%BC%D0%B0%D1%86%D0%B8%D1%8F_%D0%9B%D0%B0%D0%BF%D0%BB%D0%B0%D1%81%D0%B0_%28%D0%BF%D1%80%D0%B8%D0%BC%D0%B5%D1%80%29»
Личные инструменты