Применение интерполяции для решения уравнений
Материал из MachineLearning.
(→Интерполяция полиномами Лагранжа) |
(викификация, орфография) |
||
| Строка 63: | Строка 63: | ||
''f(x)'' = sin(''x'') на [-1, 1]. ''g(x)'' - сплайн-интерполяция синуса, функцию ''f(x)'' пытаемся представить в виде некоторых элементарных функций: | ''f(x)'' = sin(''x'') на [-1, 1]. ''g(x)'' - сплайн-интерполяция синуса, функцию ''f(x)'' пытаемся представить в виде некоторых элементарных функций: | ||
| - | <tex>f(x)=\sum_{k=0}^N {c_k\Phi_k(x)},</tex> где <tex>\{\Phi_k(x)\}</tex> — фиксированный линейно независимые функции, <tex>c_0, c_1, \cdots, c_n</tex> — не | + | <tex>f(x)=\sum_{k=0}^N {c_k\Phi_k(x)},</tex> где <tex>\{\Phi_k(x)\}</tex> — фиксированный линейно независимые функции, <tex>c_0, c_1, \cdots, c_n</tex> — не определённые пока коэффициенты. |
| - | При выборе шага ''h'' = 0.25 интерполяция | + | При выборе шага ''h'' = 0.25 интерполяция выглядит так: |
[[Изображение:Interpolation result sin 0,25.png]] | [[Изображение:Interpolation result sin 0,25.png]] | ||
| Строка 92: | Строка 92: | ||
Например, если сравнивать интерполяцию каноническим полиномом и полиномами Лагранжа, то лучше использовать второй метод, ибо он наиболее точно и с меньшими затратами приближает требуемую функцию, а сложность решения уравнения ''g(x)'' = 0 у них одинакова. | Например, если сравнивать интерполяцию каноническим полиномом и полиномами Лагранжа, то лучше использовать второй метод, ибо он наиболее точно и с меньшими затратами приближает требуемую функцию, а сложность решения уравнения ''g(x)'' = 0 у них одинакова. | ||
| - | А интерполяцию | + | А интерполяцию кубическими сплайнами рационально применять, если ''f(x)'' - периодическая или тригонометрическая функция. В случае приближения сплайнами, например, кусочно-линейной функции возникает следующий эффект: |
[[Изображение:Kusochnozadannaya.png]] | [[Изображение:Kusochnozadannaya.png]] | ||
| Строка 129: | Строка 129: | ||
* [[Тригонометрическая интерполяция]] | * [[Тригонометрическая интерполяция]] | ||
* [[Практикум ММП ВМК, 4й курс, осень 2008]] | * [[Практикум ММП ВМК, 4й курс, осень 2008]] | ||
| + | |||
| + | [[Категория:Учебные задачи]] | ||
Версия 10:16, 8 ноября 2008
|
Постановка задачи
Пусть на отрезке [a,b] задана функция f(x), и необходимо решить уравнение f(x) = 0 на этом отрезке. Известно много различных способов нахождения корней уравнения, но мы поступим следующим образом: будем приближать исходную функцию f(x) другой функцией g(x) и искать корни именно интерполированной (в англоязычной аббревиатуре - Interpolation) функции g(x).
Рассмотрим следующие методы интерполяции:
- Интерполяция каноническим полиномом
- Интерполяция полиномами Лагранжа
- Интерполяция степенными рядами
- Интерполяция кубическими сплайнами
- Тригонометрическая интерполяция
Сравнение методов
Сравним методы интерполяции функций и выясним, какой из них лучше использовать для нахождения корней уравнения f(x) = 0 в конкретном случае. В конечном итоге предстоит определить, насколько точно корни уравнения g(x) = 0 приближают корни уравнения f(x) = 0.
Интерполяция каноническим полиномом
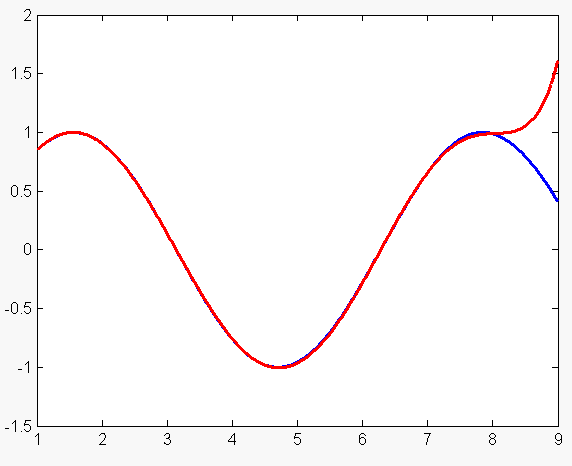
Рассмотрим в качестве функции f(x) = sin(x) на [1,8], а в качестве интерполирующей функции g(x) – полином, имеющий следующий вид:
В качестве узлов интерполяции выберем точки на отрезке [1,8] по алгоритму Чебышева. При выборе 8 узлов получается наименьшая ошибка интерполяции (она равна 0.0124).
График синуса (показан синим цветом) и интерполирующей функции (показан красным цветом) в этом случае выглядит так:
Корни полинома g(x) = 0 будем искать, например, методом Гаусса. Ошибка при нахождении поиске складывается из ошибки интерполяции и ошибки решения уравнения.
Погрешность интерполяции:
Сложность метода Гаусса: O(2n/3).
Интерполяция полиномами Лагранжа
Рассмотрим в качестве f(x) ту же функцию sin(x), но на этот раз на отрезке [-3,3], а в качестве интерполирующей функции g(x) рассмотрим полином:
где
- полиномы степени n вида
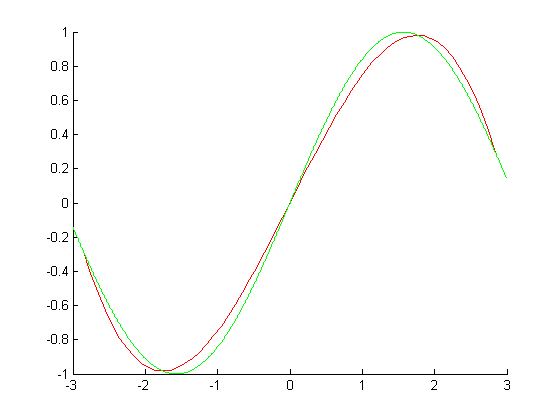
В качестве узлов интерполяции снова по алгоритму Чебышева выберем точки на отрезке [-3, 3].
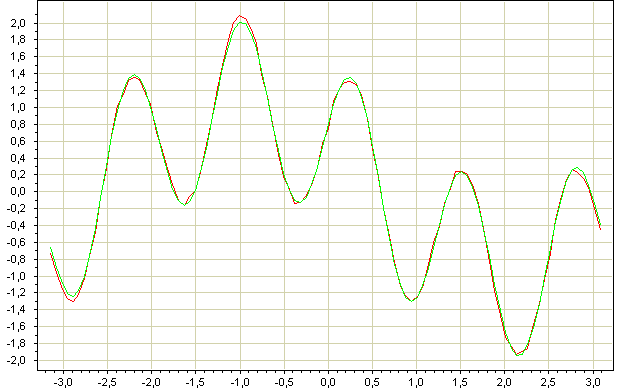
График синуса (показан красным цветом) и интерполирующей функции (показан зелёным цветом) в этом случае выглядит так:
Уравнение Лагранжа g(x) = 0 решается проще, чем f(x) = 0.
При этом ошибка приближения: 0.0944, погрешность интерполяции:
Ошибка нахождения корней снова складывается из ошибки интерполяции и ошибки решения уравнения Лагранжа.
Интерполяция степенными рядами
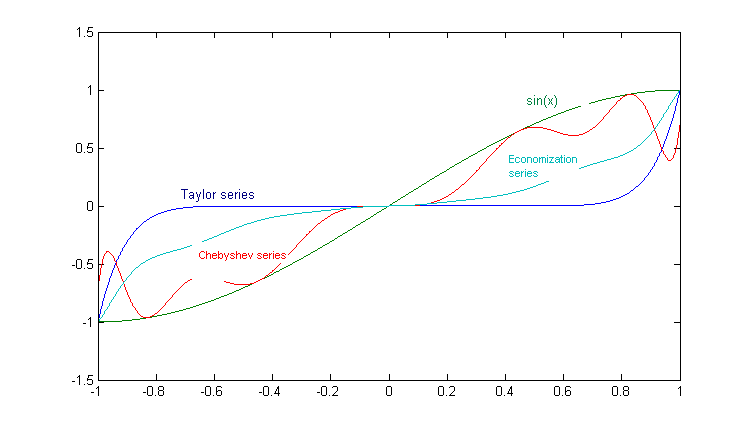
В качестве f(x) снова рассматриваем sin(x) на [-1, 1], g(x) в данном случае имеет следующий вид:
Графики показаны на следующем рисунке:
Ошибка приближения в этом случае больше, поэтому данный метод интерполяции менее предпочтителен для поиска корней, погрешность интерполяции:
Интерполяция кубическими сплайнами
f(x) = sin(x) на [-1, 1]. g(x) - сплайн-интерполяция синуса, функцию f(x) пытаемся представить в виде некоторых элементарных функций:
где
— фиксированный линейно независимые функции,
— не определённые пока коэффициенты.
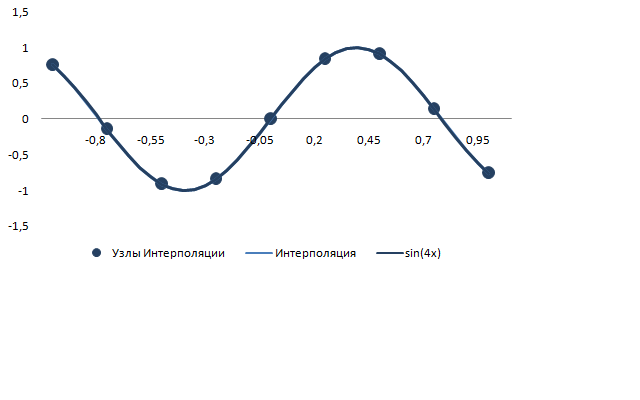
При выборе шага h = 0.25 интерполяция выглядит так:
Ошибка интерполяции оценивается как
Тригонометрическая интерполяция
На этот раз разложим функцию f(x) (считаем её непрерывно-дифференцируемой) в ряд Фурье: , где
Для её приближения будем использовать тригонометрический полином следующего вида:
Тогда приближение функции f(x) функцией g(x) будет выглядеть примерно следующим образом:
Поиск корней тригонометрической функции осуществляется итерационным методом. Анализ данного метода будет дан ниже.
Анализ методов
При решении уравнения f(x) = 0 вместо поиска корней исходной функции f(x) мы переходили к интерполирующей функции g(x) и искали её корни. Но какой же метод аппроксимации лучше для поиска корней?
Однозначного ответа на данный вопрос быть не может - это зависит от функции f(x). С одной стороны, надо использовать тот метод, который лучше приближает исходную функцию f(x). С другой стороны, мы должны достаточно точно отыскать корни g(x).
Например, если сравнивать интерполяцию каноническим полиномом и полиномами Лагранжа, то лучше использовать второй метод, ибо он наиболее точно и с меньшими затратами приближает требуемую функцию, а сложность решения уравнения g(x) = 0 у них одинакова.
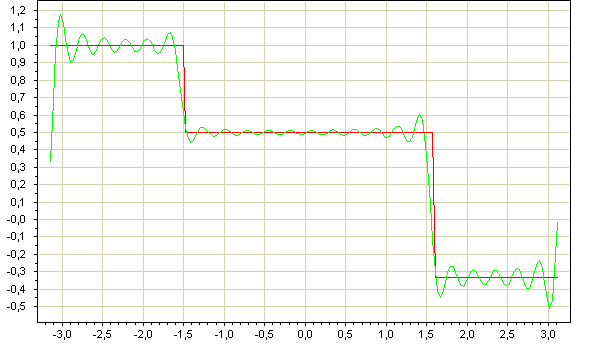
А интерполяцию кубическими сплайнами рационально применять, если f(x) - периодическая или тригонометрическая функция. В случае приближения сплайнами, например, кусочно-линейной функции возникает следующий эффект:
Понятно, что ни о какой точности решения уравнения g(x) = 0 говорить не приходится.
Вывод
Были рассмотрены следующие методы интерполяции исходной функции для решения уравнения f(x) = 0:
- Интерполяция каноническим полиномом
- Интерполяция полиномами Лагранжа
- Интерполяция степенными рядами
- Интерполяция кубическими сплайнами
- Тригонометрическая интерполяция
Установлено, что точность решения интерполяционного уравнения зависит от вида функции f(x). В результате чего в качестве рекомендации предлагается следующее:
- интерполировать функцию f(x) различными способами,
- выбрать метод, на котором достигается минимальная ошибка интерполяции,
- искать корни этого метода.
Литература
- Н.С. Бахвалов, Н.П. Жидков, Г.М. Кобельков. Численные методы. Изд-во "Лаборатория базовых знаний". Москва. 2003.
- И.С. Березин, Н.П. Жидков. Методы вычислений. Изд. ФизМатЛит. Москва. 1962.
- А.А.Самарский, А.В.Гулин. Численные методы М.: Наука, 1989.
- А.А.Самарский. Введение в численные методы М.: Наука, 1982.
- Дж. Форсайт, М.Мальком, К. Моулер. Машинные методы математических вычислений. Изд-во "Мир". Москва. 1980.