Нейрокриптография

Материал из MachineLearning.

Версия от 11:28, 29 декабря 2009; Лошкарёв Сергей (Обсуждение | вклад)

(разн.) ← Предыдущая | Текущая версия (разн.) | Следующая → (разн.)

Перейти к: навигация, поиск

Данная статья является непроверенным учебным заданием.

Студент: Участник:Лошкарёв Сергей

Преподаватель: Участник:Константин Воронцов

Срок: 8 января 2010

До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru. По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}.

См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.

Нейрокриптография это раздел криптографии, изучающий применение стохастических алгоритмов, в частности, нейронных сетей, для шифрования и криптоанализа.

Определение

В криптоанализе используется способность нейронных сетей исследовать пространство решений. Также имеется возможность создавать новые типы атак на существующие алгоритмы шифрования, основанные на том, что любая функции может быть представлена нейронной сетью. Взломав алгоритм, можно найти решение, по крайней мере, теоретически.

При этом используются такие свойства нейронных сетей, как взаимное обучение, самообучение, и стохастическое поведение, а также низкая чувствительность к шуму, неточностям(искажения данных, весовых коэффициентов, ошибки в программе). Они позволяют решать проблемы криптографии с открытым ключом, распределения ключей, хеширования и генерации псевдослучайных чисел.

Идеи нейрокриптографии впервые были озвучены Себастьяном Дорленсом (Sebastien Dourlens) в 1995 году, спустя 30 лет после определения основ нейронных сетей.

Применение

Область относительно нова, и пока не имеет практических применений. Однако уже сейчас она может использоваться там, где есть непрерывная генерация ключей. В 1995 году Себастьян Дорленс применил нейрокриптоанализ, чтобы научить нейронные сети инвертировать S-перестановки в DES. В ходе эксперимента было найдено 50 % битов ключа, то есть ключ целиком может быть найден за короткое время. Аппаратная реализация состоит из множества (64К) простых микроконтроллеров, расположенных на СБИС. Другой пример — протокол шифрования с открытым ключом Халил Шибаба (Khalil Shihab), в котором процесс дешифрации основан на многоуровневой нейронной сети, обучающейся по алгоритму обратного распространения (back propagation). В то же время процесс шифрования и создания закрытого ключа использует обычную двоичную алгебру. Преимущество этого метода в малых затратах времени и памяти. Недостаток — в алгоритме обратного распространения: на больших массивах входных данных нейронная сети обучается очень долго. Поэтому данный протокол имеет лишь теоретическое значение.

Протокол обмена ключами

Для обмена ключами между двумя абонентами наиболее часто используется алгоритм Диффи-Хеллмана. Его более безопасная замена основана на синхронизации двух древовидных машин четности (TPM, tree parity machines). Синхронизация этих машин похожа на синхронизацию двух хаотических осцилляторов в теории хаотических связей (chaos communications).

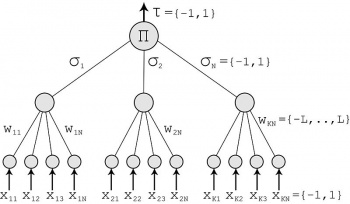
TPM

TPM - это особый вид многоуровневой нейронной сети прямого распространения.

Она состоит из одного выходного нейрона, K скрытых нейронов и K*N входных нейронов. Входные нейроны принимают двоичные значения:

$x_{ij} \in \left\{ -1,+1 \right\}$

Веса между входными и скрытыми нейронами принимают значения:

$w_{ij} \in \left\{-L,...,0,...,+L \right\}$

Значение каждого скрытого нейрона есть сумма произведений входного значения и весового коэффициента:

$\sigma_i=sgn(\sum_{j=1}^{N}w_{ij}x_{ij})$

$\sgn (x) = \begin{cases} -1 & \text{if } x =< 0, \\ 1 & \text{if } x > 0. \end{cases}$

Значение выходного нейрона есть произведение всех скрытых нейронов: </br>

$\tau=\prod_{i=1}^{K}\sigma_i$

Выходное значение также двоичное.

Протокол

У каждого абонента (А или Б) есть своя TPM. Их синхронизация происходит следующим образом:

Задаём случайные значения весовых коэффициентов
Выполняем следующие шаги, пока не наступит синхронизация
1. Генерируем случайный входной вектор X
2. Вычисляем значения скрытых нейронов
3. Вычисляем значение выходного нейрона
4. Сравниваем выходы двух TPM:
  1. Выходы разные: переход к п.2.1
  2. Выходы одинаковые: применяем выбранное правило к весовым коэффициентам

После полной синхронизации (веса w_ij обоих TPM одинаковые), А и Б могут использовать веса в качестве ключа.</br> Этот метод известен как двунаправленное обучение.</br>

Для обновления весовых коэффициентов могут использоваться следующие правила:

Правило Хеббиана:

$w_i^+=w_i+\sigma_ix_i\Theta(\sigma_i\tau)\Theta(\tau^A\tau^B)$

Анти-правило Хеббиана:

$w_i^+=w_i-\sigma_ix_i\Theta(\sigma_i\tau)\Theta(\tau^A\tau^B)$

Случайное блуждание:

$w_i^+=w_i+x_i\Theta(\sigma_i\tau)\Theta(\tau^A\tau^B)$

Виды атак и надёжность

Для каждой атаки предполагается, что криптоаналитик Е может подслушивать сообщения между А и Б, но не может их изменять.

Метод грубой силы

Криптоаналитик должен проверить все возможные варианты ключей, т.е. все возможные веса w_ij. Если имеется K скрытых нейронов, K*N входных нейронов и максимальный вес L, то это даёт (2L+1)^KN вариантов. Например, для K = 3, L = 3, N = 100 - 3*10²⁵³ различных ключей. На сегодняшний день такая атака невозможна.

Обучение собственной TPM

Пусть у криптоаналитика есть такая же TPM, как и у абонентов. Он хочет её синхронизировать с двумя другими TPM. На каждом шаге возможны три ситуации:

Output(A) ≠ Output(B): Абоненты не обновляют веса.
Output(A) = Output(B) = Output(E): Все трое обновляют веса.
Output(A) = Output(B) ≠ Output(E): А и Б обновляют веса, но Е не может этого сделать.Поэтому он обучается медленнее, чем А и Б синхронизируются.

Таким образом, криптоаналитик может определить ключ лишь с очень малой вероятностью.

Другие атаки

Защищенность обычных криптографических систем можно улучшить, увеличив длину ключа. В нейрокриптографии вместо ключа увеличивается синаптическая длина L. Это увеличивает сложность атаки экспоненциально, в то время как затраты абонентов на дешифрацию растут полиномиально. Таким образом, взлом подобной системы является NP-сложной задачей.

Алексанр Климов, Антон Митягин и Ади Шамир утверждают, что исходный алгоритм нейросинхронизации может быть сломан по крайней мере тремя видами атак: геометрической, вероятностным анализом и генетическими алгоритмами. Хотя данная реализация небезопасна, идеи случайной синхронизации могут привести к абсолютно безопасной схеме.

Защита от квантовых компьютеров

В квантовом компьютере данные хранятся в кубитах. Это позволяет решать более сложные задачи (дискретный логарифм, факторизация) за существенно меньшее время. Поэтому очень важно найти алгоритмы , не основанные на этих проблемах теории чисел. Нейронный протокол обмена ключей не основан на теории чисел, он основан на различии между однонаправленной и двунаправленной синхронизацией нейронных сетей. Поэтому, подобные протоколы могут ускорить процесс обмена.

Ссылки

Neuro-Cryptography 1995 — The first definition of the Neuro-Cryptography (AI Neural-Cryptography) applied to DES cryptanalysis by Sebastien Dourlens, France.
Neural Cryptography — Description of one kind of neural cryptography at the University of Würzburg, Germany.
Using synchronized neural networks to achieve public key authentication system — One of the leading papers that introduce the concept.
A remote password authentication scheme for multiserverarchitecture using neural networks — Possible practical application of Neural Cryptography.
Analysis of Neural Cryptography — Analysis of neural cryptography in general and focusing on the weakness and possible attacks of using synchronized neural networks.
Neural Synchronization and Cryptography — Andreas Ruttor. PhD thesis, Bayerische Julius-Maximilians-Universität Würzburg, 2006.
Genetic attack on neural cryptography
A backpropagation neural network for computer network security

Источник — «http://www.machinelearning.ru/wiki/index.php?title=%D0%9D%D0%B5%D0%B9%D1%80%D0%BE%D0%BA%D1%80%D0%B8%D0%BF%D1%82%D0%BE%D0%B3%D1%80%D0%B0%D1%84%D0%B8%D1%8F»

Категория: Непроверенные учебные задания