Аппроксимация функции ошибки
Материал из MachineLearning.
|
В работе рассматривается метод аппроксимации функции ошибки функцией многомерного нормального распределения. Рассматриваются случаи матрицы ковариации общего вида, диагональной матрицы ковариации, а также диагональной матрицы ковариации с равными значениями дисперсии. Для нормировки получившихся функций распределения используется аппроксимация Лапласа.
Постановка задачи
Дана выборка , где
- вектора независимой переменной, а
- значения зависимой переменной.
Предполагается, что
Также предполагается, что задано апостериорное распределение параметров модели , которому соответствует функция ошибки
:
Пусть - наиболее вероятные параметры модели. Требуется найти аппроксимацию Лапласа для функции
в точке
. Заметим, что в данной работе в качестве функции ошибки берется сумма квадратов ошибок аппроксимации
Описание решения
Сначала находим оптимальные значения параметров модели :
Далее необходимо найти аппроксимацию Лапласа в точке :
где - матрица, обратная к ковариационной матрице нормального распределения, а
- нормирующий коэффициент. Заметим, что в силу положительной определенности матрицы
ее можно представить в соответствии с разложением Холецкого:
, где
- верхнетреугольная матрица. Параметризуем матрицу
следующим образом:
Также параметризуем нормирующий множитель .
Получаем, что
.
Построим обучающую выборку
, где точки
берутся равномерно из окрестности наиболее вероятных параметров
, в которой мы хотим построить аппроксимацию.
Для нахождения неизвестных параметров
минимизируем квадратичный критерий для точек обучающей выборки
:
После нахождения оптимальных значений параметров полученные распределения остается отнормировать в соответствии с аппроксимацией Лапласа:
Вычислительный эксперимент
- описание эксперимента
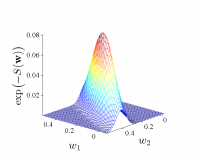
В эксперименте в качестве обучающей выборки использовался временной ряд цен на хлеб из 195 точек. Для приближения использовалась модель линейной регрессии $f(x, w) = w_1 + w_2 * x^2$. На картинках ниже графически представлены результаты (картинки скоро будут выложены).
Функция ошибки в рассмотренном случае хорошо аппроксимируется предложенным методом, причем качество аппроксимации возрастает с увеличением качества модели. Хорошее качество аппроксимации обусловлено тем, что функция ошибки в рассматриваемом примере принадлежит тому же классу, что и функция аппроксиматор.
Исходный код и полный текст работы
Смотри также
Литература
| | Данная статья является непроверенным учебным заданием.
До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru. По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}. См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе. |