Расстояние Кука
Материал из MachineLearning.
Расстояние Кука (Cook's distance) является широко используемым методом оценки влияния соответствующего наблюдения (элемента выборки) на уравнение регрессии. Эта величина показывает разницу между вычисленными коэффициентами уравнения регрессии и значениями, которые получились бы при исключении соответствующего наблюдения. В адекватной модели все расстояния Кука должны быть примерно одинаковыми; если это не так, то имеются основания считать, что соответствующее наблюдение (или наблюдения) смещает оценки коэффициентов регрессии.
Метод назван в честь американского ученого Р. Денниса Кука , который ввел данное понятие в 1977 году.
Содержание |
Определение
Расстояние Кука оценивает эффект от удаления одного (рассматриваемого) наблюдения и вычисляется по следующей формуле:
,
где
— предсказание регрессионной модели, построенной по всей выборке, получаемое для
-ого наблюдения,
— предсказание регрессионной модели, построенной по выборке без
-ого наблюдения, получаемое для
-ого наблюдения,
— количество параметров модели,
— среднеквадратичная ошибка модели.
Нахождение и удаление выбросов
Существуют различные подходы к определению выбросов с помощью расстояния Кука. Наиболее распространенной эвристикой считается , где
— количество наблюдений в выборке.
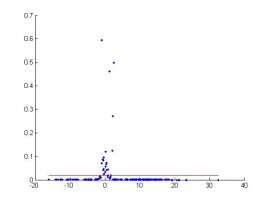
Пример использования
Рассмотрим задачу по оценке эффективность тромболитической терапии. В данной задаче собраны данные по 206 пациентам второго кардиологического отделения московской городской клинической больницы №25. Имеются результаты 14 анализов, а также 8 дополнительных признаков, описывающих пациента (пол, возраст, курение, наличие диабета и т.д.). Построив уравнение регрессии и оценив расстояние Кука, мы можем визуализировать наблюдения и определить выбросы.
Реализации
- MATLAB: В версии 2013b и выше реализован отдельный класс для обобщенной модели регрессии.
Построив модель с помощью функции mdl = fitglm(X, y), можем оценить для всех наблюдений расстояние Кука с помощью функций класса: mdl.Diagnostics.CooksDistance.
Ссылки
- Cook, R. Dennis (February 1977). "Detection of Influential Observations in Linear Regression".
- Cook, R. Dennis; and Weisberg, Sanford (1982); Residuals and influence in regression, New York, NY: Chapman & Hall
- GeneralizedLinearModel class. MATLAB R2013b Documentation.