Участник:Gukov/Песочница
Материал из MachineLearning.
Содержание |
Введение
Метод Ньютона-Рафсона
Пусть имеется некоторая функция и необходимо найти такие значения аргумента
, для которых
Перепишем (1) в виде
и запишем -ое приближения корня (1.1), при этом делая поправку
к очередному значению
где и положим
.
Тогда (2) перепишется в виде
Нетрудно видеть, что (3) эквивалентно простому методу последовательных приближений
где .
Вспомним также, что если , то метод сходится. Имеем
Но так как справедливо соотношение (1.1), то для достаточно близких к решению (1.1), выражение в скобках в числителе дроби становится малым. Поэтому итерационный метод, описываемый формулой (3) сходится, если
- 1. Начальное приближение
выбрано достаточно близко к решению
.
- 2. Производная
не становится слишком большой.
- 3. Производная
не слишком близка к 1.
Это и есть метод Ньютона-Рафсона. Обычно его записывают в виде
,
где
Таким образом, мы вернулись к уравнению в форме (1), и условия сходимости принимают следующий вид
- 1. Начальное приближение
выбрано достаточно близко к корню уравнения
.
- 2. Производная
не становится очень большой.
- 3. Производная
не слишком близка к 0.
Случай почти равных корней
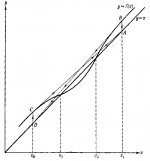
Условие 3 сходимости метода Ньютона-Рафсона означает, что никакие два корня не находятся слишком близко один к другому. Соответствующая ситуация представлена на рисунке 1 (масштаб сильно увеличен). Заметим, что производная близка
к 1 при x, равном обоим значениям корней,
и
. Более того, на основании теоремы Лагранжа, можно утверждать, что
где-то между
и
.
Рассмотрим, что случится, если принять в качестве исходного значения для корня
. Касательная,
проведенная через точку
, пересечет прямую
в точке
, и следующее приближение будет равно
. Касательная, проведенная через точку
, пересекает прямую в точке
, и в качестве следующего приближеня получается снова
. Итерационный процесс, таким образом, осциллирует между
и
до бесконечности, не сходясь ни к одному значению корня. Иначе говоря, не удается отделить эти два корня, потому что они расположены слишком близко.
Изложение метода
Экстраполяция Ричардсона
Предположим, что для вычисления интеграла (1) отрезок разбит на
равных отрезков длины
и на каждом частичном отрезке применяется одна и та жа квадратурная формула. Тогда исходный интеграл
заменяется некоторой квадратурной суммой
, причем возникающая погрешность зависит от шага сетки
.
Для некоторых квадратурных формул удается получить разложение погрешности
по степеням
. Предположим,
что для данной квадратурной суммы
существует разложение:
,
где и коэффициенты
не зависят от
.
При этом величины
предполагаются известными.
Теперь предположим:
Чтобы избавиться от степени , составляющей ошибку (ибо среди всех слагаемых, составляющих ошибку, слагамое при
является наибольшим) вычислим величину
. Имеем:
Отсюда
то есть имеем более точное приближение к интегралу .
Таким образом, рекуррентную формулу можно записать в виде:
Заметим, что - величина, на которую мы делим размер шага при каждом новом вычислении
. Разумно положить
, т.к. большие значения
могут вызвать резкое увеличение количества вычислений.
Для наглядности представим процесс экстраполирования следующей таблицей:
Метод Рунге
Пусть существует асимптотическое разложение вида:
,
где - достаточно гладкая функция, а
.
Проведем расчеты на двух равномерных сетках с шагами и
соответственно и найдем выражения
и
,
. Потребуем,
чтобы погрешность для их линейной комбинации:
была величиной более высокого порядка по сравнению с и
. Если для
имеет место формула вида
,
то для
получим
Выберем параметр \sigma из условия :
.
Имеем
,
,
причем . Так, если
, то
. Таким образом, проведя вычисления на двух сетках
с шагами
и
, мы повысили порядок точности на
(на
) для
.
Процесс Эйткена
Метод расчета на нескольких сетках применяется для повышения порядка точности даже в том случае, когда неизвестен порядок главного члена погрешности. Предположим, чт для погрешности имеет место представление
,
,
так что
Проведем вычисления на трех сетках: ,
,
(
). Определим
. При этом пренебрегаем членом
. Образуем отношение
и найдем
.
Зная приближенное значение , можно методом методом Рунге повысить порядок точности. Для этого образуем комбинацию
и выберем
так, чтобы
, то есть
.
Тогда для погрешности
получаем
.
Числовой пример
Найдем с помощью квадратурной формулы трапеций приближенное значение интеграла, применив экстраполяцию Ричардсона (данный метод называется методом Ромберга):
В нижеследующей таблице представлены результаты работы программы:
| r | Исходная формула | Экстраполированная формула | Точное значение | Погрешность вычислений | Погрешность формулы |
|---|---|---|---|---|---|
| 2 | 3.98277278 | 4.04665506 | 4.04718956 | 0.0005345 | 0.00275556 |
| 4 | 4.03068449 | 4.04714980 | 4.04718956 | 0.00003976 | 0.00017222 |
| 8 | 4.04303347 | 4.04718692 | 4.04718956 | 0.00000264 | 0.00001076 |
| 16 | 4.04614856 | 4.04718939 | 4.04718956 | 0.00000017 | 0.00000067 |
| 32 | 4.04692918 | 4.04718955 | 4.04718956 | 0.00000001 | 0.00000004 |
| 64 | 4.04712446 | 4.04718956 | 4.04718956 | 0 | 0 |
| 20384 | 4.04718956 |
Здесь - коэффициент измельчения шага
. Исходная величина шага
.
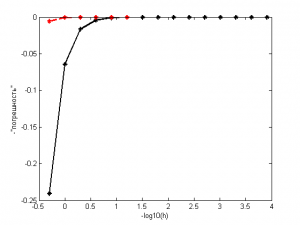
На иллюстрации черная сплошная линия - исходная формула, красная пунктирная - экстраполированная.
Как мы видим, разница между экстраполированными и неэкстраполированными результатами значительна. Уже при величине шага в мы можем найти значение интеграла с точностью
, тогда как в исходной формуле нам для достижения такой точности пришлось бы задать величину шага
.
Рекомендации программисту
Программируя экстраполяцию Ричардсона следует предпочесть итерацию рекурсии. Также реализуя многократное экстраполирование итеративно, нам не нужно хранить всю таблицу значений - достаточно иметь в распоряжении два последних столбца.
Заключение
Мы получили более точные результаты при меньшем количестве вычислений функции, чем в исходном методе. Избавившись от степени, составляющей ошибку, мы пришли к результату, который в противном случае был бы недостижим без значительного уменьшения размера шага. Таким образом, мы преобразовали весьма посредственный алгоритм вычисления интегралов в довольно эффективный.
Список литературы
- А.А.Самарский, А.В.Гулин. Численные методы М.: Наука, 1989.
- Fundamental Methods of Numerical Extrapolation With Applications, mit.edu