Машина опорных векторов

Материал из MachineLearning.

Версия от 21:17, 24 октября 2018; KorolevN (Обсуждение | вклад)

(разн.) ← Предыдущая | Текущая версия (разн.) | Следующая → (разн.)

Машина опорных векторов — является одной из наиболее популярных методологий обучения по прецедентам, предложенной В. Н. Вапником и известной в англоязычной литературе под названием SVM (Support Vector Machine).

Оптимальная разделяющая гиперплоскость. Понятие зазора между классами (margin). Случай линейной разделимости. Задача квадратичного программирования. Опорные векторы. Случай отсутствия линейной разделимости. Функции ядра (kernel functions), спрямляющее пространство, теорема Мерсера. Способы построения ядер. Примеры ядер. Сопоставление SVM и нейронной RBF-сети. Обучение SVM методом активных ограничений. SVM-регрессия.

Содержание

1 Машина опорных векторов в задачах классификации
2 Машина опорных векторов в задачах регрессии
3 Мультиклассовый метод опорных векторов
4 Программные реализации
5 Литература
6 Ссылки

Машина опорных векторов в задачах классификации

Понятие оптимальной разделяющей гиперплоскости

Линейный классификатор

Линейно разделимая выборка

Рассмотрим задачу нахождения наилучшего в некотором смысле разделения множества векторов на два класса с помощью линейной решающей функции. Пусть имеется множество прецедентов $(\Xi ,Y)$ , где $\Xi = \{ {\bf{x}}_1 ,...,{\bf{x}}_N \}$ — обучающая выборка, а $Y = (y_1 ,...,y_N )$ — множество меток двух классов $\omega _1$ и $\omega _2$ . Требуется по обучающей выборке построить линейную решающую функции, т.е. такую линейную функцию $f({\bf{x}})$ , которая удовлетворяла бы условию

$f({\bf{x}}_i ) > 0$ для всех ${\bf{x}}_i \in \omega _1$ ,

$f({\bf{x}}_i ) < 0$ для всех ${\bf{x}}_i \in \omega _2$ .

Без ограничения общности можно считать, что метки классов равны

$y_i = \left\{\:\;1,\;{\bf{x}}_i \in \varpi _1 , \\- 1,\;{\bf{x}}_i \in \varpi _2 . \right.$

Тогда поставленную выше задачу можно переформулировать следующим образом. Требуется найти линейную решающую функцию $f({\bf{x}})$ , которая бы удовлетворяла условию

(1)

$y_i f({\bf{x}}_i ) > 0$ для всех ${\bf{x}}_i \in \Xi$

Умножая, если нужно, функцию $f$ на некоторое положительное число, нетрудно видеть, что система неравенств (1) равносильна системе

$y_i f({\bf{x}}_i ) > 1$ для всех ${\bf{x}}_i \in \Xi$ .

Кроме того, так как $f({\bf{x}})$ — линейная функция, то последняя система неравенств примет вид

(2)

$y_i (({\bf{w}},{\bf{x}}_i ) + b) \ge 1,\quad i = 1,...,N$ ,

где ${\bf{w}}$ — вектор весовых коэффициентов, $b$ — некоторое число. Тогда разделяющей два класса гиперплоскостью будет $({\bf{w}},{\bf{x}}) + b = 0$ . Нетрудно видеть, что и все гиперплоскости вида $({\bf{w}},{\bf{x}}) + b' = 0$ , где $b' \in (b - 1,b + 1)$ , также будут разделяющими (рис.1). Расстояние между граничными гиперплоскостями $({\bf{w}},{\bf{x}}) + b - 1 = 0$ и $({\bf{w}},{\bf{x}}) + b + 1 = 0$ равно ${{\frac {{2}}{{\left\| {\bf{w}} \right\|}}$ . Действительно, $\left( {\frac{{\bf{w}}}{{\left\| {\bf{w}} \right\|}},{\bf{x}}} \right) + \frac{{b - 1}}{{\left\| {\bf{w}} \right\|}} = 0$ и $\left( {\frac{{\bf{w}}}{{\left\| {\bf{w}} \right\|}},{\bf{x}}} \right) + \frac{{b + 1}}{{\left\| {\bf{w}} \right\|}} = 0$ — нормальные уравнения этих гиперплоскостей. Тогда $p_1 = \frac{{b - 1}}{{\left\| {\bf{w}} \right\|}}$ и $p_2 = \frac{{b + 1}}{{\left\| {\bf{w}} \right\|}}$ — расстояния от этих гиперплоскостей до начала координат и ${{\frac {{2}}{{\left\| {\bf{w}} \right\|}}$ — расстояние между гиперплоскостями. На самих граничных плоскостях может находиться некоторое число обучающих векторов. Эти векторы называются опорными.

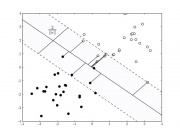
Для надежного разделения классов необходимо, чтобы расстояние между разделяющими гиперплоскостями было как можно большим, т.е. $\left\| {\bf{w}} \right\|$ была как можно меньше. Таким образом, ставится задача нахождения минимума квадратичного функционала $0.5({\bf{w}},{\bf{w}})$ (коэффициент 0.5 вводится для удобства дифференцирования) в выпуклом многограннике, задаваемым системой неравенств (2). В выпуклом множестве квадратичный функционал всегда имеет единственный минимум (если это множество не пусто). Из теоремы Куна — Таккера следует, что решение этой оптимизационной задачи равносильно поиску седловой точки лагранжиана

$L({\bf{w}},b,{\bf{\lambda }}) = 0.5({\bf{w}},{\bf{w}}) - \sum\limits_{i = 1}^N {\lambda _i (y_i (({\bf{w}},{\bf{x}}_i ) + b) - 1)} \to \ {\min }\limits_{{\bf{w}},b} \ {\max }\limits_{\bf{\lambda }}$

в ортанте по множителям Лагранжа $\lambda _i \ge 0\;\;(i = 1,...,N)$ , при условии, что

$\lambda _i \left( {y_i (({\bf{w}},{\bf{x}}_i ) + b) - 1} \right) = 0,\quad i = 1,...,N$ .

Последнее условие равносильно тому, что

(3)

$\lambda _i = 0$ или $y_i (({\bf{w}},{\bf{x}}_i ) + b) - 1 = 0,\quad i = 1,...,N$

Из необходимых условий существования седловой точки (полагая ${\bf{x}}_i = (x_{i1} ,x_{i2} ,...,x_{in} )$ ) имеем

$\left\{ {\begin{matrix} 0 = \frac{{\partial L}}{{\partial w_j }} = w_j - \sum\limits_{i = 1}^N {\lambda _i y_i x_{ij} } ,\quad j = 1,...,n, \\ 0 = \frac{{\partial L}}{{\partial b}} = \sum\limits_{i = 1}^N {\lambda _i y_i } . \\\end{matrix}} \right\.$

Откуда следует, что вектор ${\bf{w}}$ следует искать в виде

(4)

${\bf{w}} = \sum\limits_{i = 1}^N {\lambda _i y_i {\bf{x}}_i }$ ,

причем

(5)

$\sum\limits_{i = 1}^N {\lambda _i y_i } = 0$ .

В силу (3) в сумму (4) с ненулевыми коэффициентами $\lambda _i$ входят только те векторы, для которых $y_i (({\bf{w}},{\bf{x}}_i ) + b) - 1 = 0$ . Такие векторы называют опорными, так как это именно те векторы, через которые будут проходить граничные гиперплоскости, разделяющие классы. Для найденного весового вектора ${\bf{w}}$ смещение $b$ можно вычислить как $b = {y_s}^{-1} - ({\bf{w}},{\bf{x}}_s )$ для любого опорного вектора ${\bf{x}}_s$ .

Найдем значения множителей Лагранжа, как критических точек лагранжиана. Для этого подставим (4) и (5) в лагранжиан, получим

$L({\bf{w}},b,{\bf{\lambda }}) = 0.5({\bf{w}},{\bf{w}}) - \sum\limits_{i = 1}^N {\lambda _i (y_i (({\bf{w}},{\bf{x}}_i ) + b) - 1)} =$

$0.5({\bf{w}},{\bf{w}}) - \left( {({\bf{w}},{\bf{w}}) - \sum\limits_{i = 1}^N {\lambda _i } } \right) = \sum\limits_{i = 1}^N {\lambda _i } - 0.5({\bf{w}},{\bf{w}}) =$

$\sum\limits_{i = 1}^N {\lambda _i } - 0.5\sum\limits_{i,j = 1}^N {\lambda _i \lambda _j y_i y_j ({\bf{x}}_i ,{\bf{x}}_j )} = \sum\limits_{i = 1}^N {\lambda _i } - 0.5\left\| {\sum\limits_{i = 1}^N {\lambda _i y_i {\bf{x}}_i } } \right\|^2$ .

Таким образом, задача сводится к нахождению критических точек функции

(6)

$\Phi ({\bf{\lambda }}) = \sum\limits_{i = 1}^N {\lambda _i } - 0.5\left\| {\sum\limits_{i = 1}^N {\lambda _i y_i {\bf{x}}_i } } \right\|^2$ .

Так как эта функция представляет собой разность линейной и квадратичной функций, причем квадратичная функция отрицательно определена, то требуется найти наибольшее значение функции $\Phi ({\bf{\lambda }})$ при условии $\sum\nolimits_{i = 1}^N {\lambda _i y_i } = 0$ в области $\lambda _i \ge 0\;\;(i = 1,...,N)$ . Существует много алгоритмов (в теории оптимизации) решения этой задачи (например, градиентные методы, метод покоординатного спуска и т.д.).

Замечания.

Суммирования в (6) осуществляются не по всем векторам, а только по опорным, которых может быть гораздо меньше, чем обучающих.
Линейная решающая функция в результате имеет вид $f({\bf{x}}) = \textstyle\sum_{i} {\lambda _i y_i ({\bf{x}}_i ,{\bf{x}})} + y_r^{ - 1} - \textstyle\sum_{i} {\lambda _i y_i ({\bf{x}}_i ,{\bf{x}}_r )}$ , где $\lambda _i$ зависят только $y_i$ и от значений скалярного произведения $({\bf{x}}_i ,{\bf{x}}_j )$ , причем суммирования осуществляются только по опорным векторам.
После того, как решающая функция $f({\bf{x}})$ вычислена, вектор ${\bf{x}}$ следует относить классу $\omega _1$ , если $f({\bf{x}}) > 0$ и классу $\omega _2$ , если $f({\bf{x}}) < 0$ . Вероятность неправильной классификации можно оценить с помощью некоторой непрерывно убывающей функции $\varphi (t)$ , удовлетворяющей условиям: $\varphi (0) = 0.5$ , $\varphi (t) \to 0$ при $t \to \infty$ . Тогда вероятность $p({\bf{x}})$ неправильной классификации вектора ${\bf{x}}$ будет равна $\varphi \left( {\rho ({\bf{x}},L_i )} \right)$ , если ${\bf{x}} \in \omega _i$ ( $i = 1,2$ ), где ${L_i}$ : $({\bf{w}},{\bf{x}}) + b + {{\rm sgn}} (\alpha - i) = 0$ , $1 < \alpha < 2$ . То есть $p({\bf{x}}) = \varphi \left( {\left| {\left( {\frac{{\bf{w}}}{{\left\| {\bf{w}} \right\|}},{\bf{x}}} \right) + \frac{{b + {{\rm sgn}} (\alpha - i)}}{{\left\| {\bf{w}} \right\|}}} \right|} \right)$ , если ${\bf{x}} \in \omega _i$ $(i = 1,2)$ .
В такой постановке алгоритм линейный классификации был разработан В. Вапником в 1963 году.

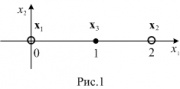
Пример. Методом опорных векторов разделите классы $\omega _1 = \left\{ {{\bf{x}}_1 } \right\}$ и $\omega _2 = \left\{ {{\bf{x}}_2 ,{\bf{x}}_3 } \right\}$ , если ${\bf{x}}_1 = (1,1)^T$ , ${\bf{x}}_2 = (1,2)^T$ , ${\bf{x}}_3 = (2,3)^T$ .

Решение. Положим $y_1 = 1$ , $y_2 = - 1$ , $y_3 = - 1$ . Тогда функция $\Phi ({\bf{\lambda }})$ будет иметь вид

$\Phi ({\bf{\lambda }}) = \sum\limits_{i = 1}^3 {\lambda _i } - 0.5\sum\limits_{i,j = 1}^3 {\lambda _i \lambda _j y_i y_j ({\bf{x}}_i ,{\bf{x}}_j )} =$ $\lambda _1 + \lambda _2 + \lambda _3 - 0.5(2\lambda _1^2 + 5\lambda _2^2 + 13\lambda _3^2 - 6\lambda _1 \lambda _2 - 10\lambda _1 \lambda _3 + 16\lambda _2 \lambda _3 )$ ,

причем $\lambda _1 - \lambda _2 - \lambda _3 = 0 \Rightarrow \lambda _3 = \lambda _1 - \lambda _2$ . Тогда $\Phi (\lambda _1 ,\lambda _2 ) = 2\lambda _1 - 2.5\lambda _1^2 - \lambda _2^2 + 3\lambda _1 \lambda _2$ . Составим и решим нормальную систему для функции $\Phi (\lambda _1 ,\lambda _2 )$ :

$\left\{ \begin{matrix}{l}\frac{{\partial \Phi }}{{\partial \lambda _1 }} = 0, \\ \frac{{\partial \Phi }}{{\partial \lambda _2 }} = 0 \\ \end{matrix} \right. \Leftrightarrow \left\{ \begin{matrix}{l} 2 - 5\lambda _1 + 3\lambda _2 = 0, \\ - 2\lambda _2 + \lambda _1 = 0 \\ \end{matrix} \right. \Leftrightarrow \left\{ \begin{matrix}{l} \lambda _1 = 4, \\ \lambda _2 = 6. \\ \end{matrix} \right.$

Следовательно, $\lambda _1 = 4$ , $\lambda _2 = 6$ , $\lambda _3 = - 2$ . Так как $\lambda _3 < 0$ , то исследуем функцию $\Phi ({\bf{\lambda }})$ на границе области $\lambda _i \ge 0\;\;(i = 1,2,3)$ при условии $\lambda _3 = \lambda _1 - \lambda _2$ . Если $\lambda _1 = 0$ , то $\lambda _3 = - \lambda _2 \Rightarrow \lambda _i^{(1)} = 0\;\;(i = 1,2,3) \Rightarrow \Phi ({\bf{\lambda }}^{(1)} ) = 0$ . Пусть $\lambda _2 = 0$ . Тогда $\lambda _1 = \lambda _3 = \lambda$ и $\Phi (\lambda ) = 2\lambda - 2.5\lambda ^2$ , $\Phi '(\lambda ) = 0$ при $\lambda ^{(2)} = {2/5}$ . Следовательно, $\lambda _1^{(2)} = \lambda _3^{(2)} = {2/5}$ , $\lambda _2^{(2)} = 0$ и $\Phi ({\bf{\lambda }}^{(2)} ) = {2/5}$ .

Если же $\lambda _3 = 0$ , то $\lambda _1 = \lambda _2 = \lambda$ и $\Phi (\lambda ) = 2\lambda - 0.5\lambda ^2$ , $\Phi '(\lambda ) = 0$ при $\lambda ^{(3)} = 2$ . Следовательно, $\lambda _1^{(3)} = \lambda _2^{(3)} = 2$ , $\lambda _3^{(3)} = 0$ и $\Phi ({\bf{\lambda }}^{(3)} ) = 2$ .

Таким образом, наибольшее значение функции $\Phi ({\bf{\lambda }})$ в области $\lambda _i \ge 0$ $(i = 1,2,3)$ при условии $\lambda _3 = \lambda _1 - \lambda _2$ достигается в точке ${\bf{\lambda }}^{(3)} = \left( {2,2,0} \right)^T$ . В этом случае,

$\left{ \begin{matrix}{l} \bf{w} = \sum\limits_{i = 1}^3 {\lambda _i y_i {\bf{x}}_i } = 2{\bf{x}}_1 - 2{\bf{x}}_2 = 2\left( \begin{matrix} 1 \\ 1 \\ \end{matrix} \right) - 2\left( \begin{matrix}1\\ 2 \\ \end{matrix} \right) = \left( \begin{matrix} 0 \\ - 2 \\ \end{matrix} \right ),\\ b = \frac {1} {{y_1 }} - ({\bf{w}},{\bf{x}}_1 ) = 1 - (0 - 2) = 3. \end{matrix}\right.$

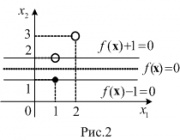
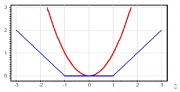
Таким образом, $f({\bf{x}}) = ({\bf{w}},{\bf{x}}) + b = - 2x_2 + 3$ и $f({\bf{x}}) = 0 \Leftrightarrow x_2 = 1.5$ . Ширина разделяющей полосы будет равна ${{\frac {{2}}{{\left\| {\bf{w}} \right\|}}$ , а прямые $f({\bf{x}}) + 1 = 0 \Leftrightarrow f({\bf{x}}) = 0 \Leftrightarrow x_2 = 2$ и $f({\bf{x}}) - 1 = 0 \Leftrightarrow x_2 = 1$ будут ее границами (см. рис.2).

Линейно неразделимая выборка

В 1992 году в работе Бернарда Бозера (Boser B.), Изабелл Гийон (Guyon I.) и Владимира Вапника был предложен способ адаптации машины опорных векторов для нелинейного разделения классов. В этом случае нужно вложить пространство признаков $R^n$ в пространство $H$ большей размерности с помощью отображения $\varphi:R^n \to H$ . Будем считать, что $H$ пространство со скалярным произведением. Тогда, рассматривая алгоритм опорных векторов для образов $\varphi ({\bf{x}}_i )$ обучающей выборки, сведем решение задачи к линейно разделимому случаю, т.е. разделяющую функцию будем искать в виде

$f({\bf{x}}) = \left( {{\bf{w}},\varphi ({\bf{x}})} \right) + b$ , ${\bf{w}} = \sum\limits_{i = 1}^N {\lambda _i y_i \varphi ({\bf{x}}_i )}$ ,

где коэффициенты $\lambda _i$ зависят от $y_i$ и от значения $\left( {\varphi ({\bf{x}}_i ),\varphi ({\bf{x}}_j )} \right)$ . Таким образом, для нахождения решающей функции нужно знать значения скалярных произведений $\left( {\varphi ({\bf{x}}_i ),\varphi ({\bf{x}}_j )} \right)$ . Для этого исследуем свойства функции $K({\bf{x}},{\bf{y}}) = \left( {\varphi ({\bf{x}}),\varphi ({\bf{y}})} \right)$ , которая называется ядром. Следующая теорема, известная в теории интегральных операторов и доказанная Джеймсом Мерсером в 1909 году, полностью характеризует ядро.

Теорема 1. Функция $K({\bf{x}},{\bf{y}})$ является ядром тогда и только тогда, когда она удовлетворяет условиям:

$K({\bf{x}},{\bf{y}}) = K({\bf{y}},{\bf{x}})$ (симметричность);
$K({\bf{x}},{\bf{y}})$ неотрицательно определена, т.е. матрица $K = (K_{i,j} )$ , $K_{i,j} = K({\bf{x}}_i ,{\bf{x}}_j )$ является неотрицательно определенной для любых векторов ${\bf{x}}_1 ,...,{\bf{x}}_m$ .

Упражнение. Докажите, что следующие функции являются ядрами:

$K({\bf{x}},{\bf{y}}) = ({\bf{x}},{\bf{y}})$ ;
$K({\bf{x}},{\bf{y}}) = \varphi ({\bf{x}})\varphi ({\bf{y}})$ ;
$K({\bf{x}},{\bf{y}}) = C > 0$ .

Теорема 2. Справедливы следующие свойства ядер:

сумма ядер – ядро;
произведение ядер – ядро;
сумма равномерно сходящегося ряда ядер – ядро;
композиция ядра и любого отображения (т.е. $K(\psi ({\bf{x}}),\psi ({\bf{y}}))$ ) – ядро.

Следствие.

многочлен с положительными коэффициентами от ядра – ядро;
экспонента от ядра – ядро;
функция $e^{ - \left\| {{\bf{x}} - {\bf{y}}} \right\|^2 }$ ядро.

Доказательство. Утверждения 1 и 2 следуют из пунктов 1, 2 и 3 теоремы. Справедливость утверждения 3 вытекает из того, что $e^{ - \left\| {{\bf{x}} - {\bf{y}}} \right\|^2 } = e^{ - (x_1 - y_1 )^2 } \cdot ... \cdot e^{ - (x_n - y_n )^2 }$ , а симметричность и положительная определенность функций $e^{ - (x_i - y_i )^2 }$ проверяется непосредственно.

Любые $m + 1$ векторов могут быть разделены на любые два класса с помощью мономиального отображения степени не больше $m$ . Поэтому, если $\varphi:{\bf{x}} \to \left\{ {x_1^{i_1 } ...x_n^{i_n } } \right\}$ , $i_1 + ... + i_n \le m$ такое отображение, то ядро, соответствующее этому отображению можно искать в виде

$K({\bf{x}},{\bf{y}}) = \left( {\varphi ({\bf{x}}),\varphi ({\bf{y}})} \right) = \left( {({\bf{x}},{\bf{y}}) + 1} \right)^m$ .

Таким образом, это ядро гарантирует разделение любых $m + 1$ векторов на любые два класса. В этом случае нахождение разделяющих функций осуществляется следующим образом:

1) найдем наибольшее значение функции

$\Phi ({\bf{\lambda }}) = \sum\nolimits_{i = 1}^N {\lambda _i } - 0.5\sum\nolimits_{i,j = 1}^N {\lambda _i \lambda _j y_i y_j K({\bf{x}}_i ,{\bf{x}}_j )}$

при условии $\sum\nolimits_{i = 1}^N {\lambda _i y_i } = 0$ в области $\lambda _i \ge 0\;\;(i = 1,...,N)$ , получим вектор ${\bf{\lambda }}^{(0)} = \left( {\lambda _1^{(0)} ,...,\lambda _N^{(0)} } \right)$ ;

2) разделяющую функцию ищем в виде

$f({\bf{x}}) = ({\bf{w}},\varphi ({\bf{x}})) + b = \left( {\sum\nolimits_{i = 1}^N {\lambda _i^0 y_i \varphi ({\bf{x}}_i )} ,\varphi ({\bf{x}})} \right) + b =$

$\sum\nolimits_{i = 1}^N {\lambda _i^0 y_i \left( {\varphi ({\bf{x}}_i ),\varphi ({\bf{x}})} \right)} + y_r^{ - 1} - \sum\nolimits_{i = 1}^N {\lambda _i^0 y_i \left( {\varphi ({\bf{x}}_i ),\varphi ({\bf{x}}_r )} \right)} =$

$\sum\nolimits_{i = 1}^N {\lambda _i^0 y_i K({\bf{x}}_i ,{\bf{x}})} + y_r^{ - 1} - \sum\nolimits_{i = 1}^N {\lambda _i^0 y_i K({\bf{x}}_i ,{\bf{x}}_r )}$ .

Преимущества и недостатки SVM:

это наиболее быстрый метод нахождения решающих функций;
метод сводится к решению задачи квадратичного программирования в выпуклой области, которая всегда имеет единственное решение;
метод находит разделяющую полосу максимальной ширины, что позволяет в дальнейшем осуществлять более уверенную классификацию;
метод чувствителен к шумам и стандартизации данных;
не существует общего подхода к автоматическому выбору ядра (и построению спрямляющего подпространства в целом) в случае линейной неразделимости классов.

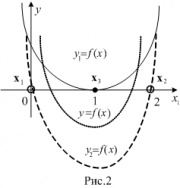
Пример. Методом опорных векторов разделите классы $\omega _1 = \left\{ {{\bf{x}}_1 ,{\bf{x}}_2 } \right\}$ и $\omega _2 = \left\{ {{\bf{x}}_3 } \right\}$ , если ${\bf{x}}_1 = (0,0)^T$ , ${\bf{x}}_2 = (2,0)^T$ , ${\bf{x}}_3 = (1,0)^T$ (рис.1).

Решение. Так как количество векторов обучающей выборки равно трем, то $m = 2$ и в качестве ядра возьмем функцию $K({\bf{x}},{\bf{y}}) = (({\bf{x}},{\bf{y}}) + 1)^2$ . Тогда

$\Phi ({\bf{\lambda }}) = \lambda _1 + \lambda _2 + \lambda _3 - 0.5(\lambda _1^2 + 25\lambda _2^2 + 4\lambda _3^2 + 2\lambda _1 \lambda _2 - 2\lambda _1 \lambda _3 - 18\lambda _2 \lambda _3 ) = \left| \begin{matrix}{l} \\ \lambda _1 + \lambda _2 =\lambda _3\\\\\end{matrix}\right|=$ $2\lambda _1 + 2\lambda _2 - 0.5(3\lambda _1^2 + 11\lambda _2^2 - 10\lambda _1 \lambda _2 )$ .

Составим нормальную систему

$\left\{\begin{matrix}{l}\frac{{\partial\Phi}}{{\partial\lambda_1}}=0,\\\frac{{\partial\Phi}}{{\partial\lambda_2}}=0\\\end{matrix}\right.\Leftrightarrow\left\{\begin{matrix}{l}2-3\lambda_1 + 5\lambda_2=0,\\2-11\lambda_2+5\lambda_1=0\\\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}{l}\lambda_1^{(0)}= 4,\\\lambda_2^{(0)}=2,\\\lambda_3^{(0)}=6.\\\end{matrix}\right.$

Можно показать, что в точке ${\bf{\lambda }}^{(0)}$ будет достигаться наибольшее значение функции $\Phi ({\bf{\lambda }})$ при условии $\lambda _1 + \lambda _2 = \lambda _3$ в области $\lambda _i \ge 0\;\;(i = 1,2,3)$ . Следовательно,

$f({\bf{x}}) = 4K({\bf{x}}_1 ,{\bf{x}}) + 2K({\bf{x}}_2 ,{\bf{x}}) - 6K({\bf{x}}_3 ,{\bf{x}}) + 1 -$ $\left({4K({\bf{x}}_1 ,{\bf{x}}_1 ) + 2K({\bf{x}}_2 ,{\bf{x}}_1 ) - 6K({\bf{x}}_3 ,{\bf{x}}_1 )} \right) =$

$4 \cdot 1 + 2(2x_1 + 1)^2 - 6(x_1 + 1)^2 + 1 -$ $(4 + 2 - 6) = 2x_1^2 - 4x_1 + 1$ .

Таким образом, $f({\bf{x}}) = 2x_1^2 - 4x_1 + 1$ и $f({\bf{x}}) = 0 \Leftrightarrow x_1 = 1 \pm {{\sqrt 2 }/2$ , $f_1 ({\bf{x}}) = f({\bf{x}}) + 1 = (x_1 - 1)^2$ , $f_2 ({\bf{x}}) = f({\bf{x}}) - 1 =$ $2x_1 (x_1 - 2)$ .

Тогда $f_1 ({\bf{x}}) = 0 \Leftrightarrow$ $x_1 = 1$ , $f_2 ({\bf{x}}) = 0 \Leftrightarrow x_1 = 0$ или $x_1 = 2$ . Если рассмотреть вложение двумерного пространства признаков в трехмерное по правилу $(x_1 ,x_2 ) \to (x_1 ,x_2 ,y)$ и проекцию последнего на плоскость $x_1 Oy$ , то можно проиллюстрировать разделение элементов обучающей выборки графиками функций $y = f(x_1 )$ , $y = f_i (x_1 )$ $(i = 1,2)$ (см. рис.2).

Ядра и спрямляющие пространства

Наиболее распространенные ядра:

Полиномиальное: $k(\mathbf{x},\mathbf{x}')=(\mathbf{x} \cdot \mathbf{x'})^d$
Полиномиальное: $k(\mathbf{x},\mathbf{x}')=(\mathbf{x} \cdot \mathbf{x'} + 1)^d$
Радиальное: $k(\mathbf{x},\mathbf{x}')=\exp(-\gamma \|\mathbf{x} - \mathbf{x'}\|^2)$ , для $\gamma > 0$

Алгоритмы настройки

Машина опорных векторов в задачах регрессии

Постановка задачи

Синяя - функция потерь $\mathcal{L}(y,g(x))$

Ставится задача регрессии: Дана обучающая выборка $X=\{(x_i,y_i)\}_{i=1}^l$ , где $x_i$ -признаковое описание i-го объекта, $y_i$ - характеристика, приписываемая объекту. Целью является поиск такой функции $g(\mathbf{x})$ , которая бы аппроксимировала выборку наилучшим образом. Задана функция потерь $\mathcal{L}(y,g(\mathbf{x}))= \begin{cases} 0, & \mbox{ } \mid y-g(x)\mid \le \epsilon\\ \mid y-g(x)\mid - \epsilon, & \mbox{ } \mid y-g(x)\mid > \epsilon \end{cases}$ , где $\epsilon>0$ определяет допустимое отклонение для результата. Считается, что этот параметр задает эксперт.

Анализ задачи

Будем искать решение задачи регрессии в линейном случае: $f(x) = (w,\mathbf{x})-w_0$ . Функция потерь принимает вид $a(x_i)=\mid (w,x_i)-w_0-y_i \mid_\epsilon$ для каждого вектора $(x_i,y_i)$ , где $\mid z \mid_\epsilon = max(0,\mid z \mid-\epsilon)$ .

В таком случае функционал потерь принимает вид

$Q_\epsilon(a,X)=\sum_{i=1}^l \mid (w,x_i)-w_0-y_i \mid_\epsilon + \tau (w,w)^2 \rightarrow \underset{w,w_0}{min}$ .

Последнее слагаемое удерживает коэффициенты $w$ от бесконечного возрастания. Как и в задаче классификации, решение зависит от скалярного произведения объектов, а не от самих объектов. Минимизация в данном случае эквивалентна задаче квадаратичного программирования с ограничениями типа неравенств. Покажем это. Положим $C=\frac{1}{2\tau}$ , и введем дополнительные переменные $\xi_i^+$ и $\xi_i^-$ , значения которых равны потере при завышенном и заниженном ответах соответственно

$\xi_i^+=(a(x_i)-y_i-\epsilon)_+$ , $\xi_i^-=(-a(x_i)+y_i-\epsilon)_-$ , $i=1,...,l$ .

Теперь мы можем записать задачу минимизации в виде задачи квадратичного программирования.

$\begin{cases} \frac{1}{2} (w,w)^2 + C\sum_{i=1}^l(\xi_i^+ + \xi_i^-)\rightarrow \underset{w,w_0,\xi_i^+,\xi_i^-}{min}, \\ (w,x_i)-w_0 \le y_i + \epsilon + \xi_i^+, & i=1,..,l; \\ (w,x_i)-w_0 \ge y_i - \epsilon - \xi_i^-, & i=1,..,l; \\ \xi_i^- \ge 0, \mbox{ } i=1,..,l; \\ \xi_i^+ \ge 0, \mbox{ } i=1,..,l; \\ \end{cases}$

Опорные векторы и двойственная задача

Как и в задаче классификации решается двойственная задача. Лагранжиан задается через двойственные переменные $\lambda_i^+, \lambda_i^-, i=1,...,l$ , а скалярные произведения можно заменить ядром $K(x_i,x_j)$

Получим результат:

$\begin{cases} \mathcal{L}(\lambda^+, \lambda^-)=-\epsilon \sum_{i=1}^l (\lambda_i^+ + \lambda_i^-)+\sum_{i=1}^l (\lambda_i^- - \lambda_i^+)y_i - \frac{1}{2}\sum_{i,j=1}^l (\lambda_i^- - \lambda_i^+)(\lambda_j^- - \lambda_j^+)K(x_i,x_j) \rightarrow \underset{\lambda^+,\lambda^-}{max}, \\ 0 \le \lambda_i^+ \le C,\mbox{ } i=1,...,l \\ 0 \le \lambda_i^- \le C,\mbox{ } i=1,...,l \\ \sum_{i=1}^l (\lambda_i^+ + \lambda_i^-) = 0;\\ \end{cases}$

Таким образом, все объекты $x_i, i=1,...,l$ делятся на 5 типов:

$1. \mid a(x_i)-y_i \mid < \epsilon;\mbox{ } \lambda_i^+=\lambda_i^-=\xi_i^+=\xi_i^-=0;$
$2. a(x_i)=y_i + \epsilon;\mbox{ }0 < \lambda_i^+ < C,\mbox{ } \lambda_i^-=\xi_i^+=\xi_i^-=0;\\$
$3. a(x_i)=y_i + \epsilon;\mbox{ }0 < \lambda_i^- < C,\mbox{ } \lambda_i^+=\xi_i^+=\xi_i^-=0;\\$
$4. a(x_i)>y_i + \epsilon;\mbox{ }\lambda_i^+ = C,\mbox{ } \lambda_i^-=0,\mbox{ }\xi_i^+=a(x_i) - y_i - \epsilon,\mbox{ } \xi_i^-=0;\\$
$5. a(x_i)<y_i - \epsilon;\mbox{ }\lambda_i^+ = 0,\mbox{ } \lambda_i^-=C,\mbox{ }\xi_i^+=0,\mbox{ } \xi_i^-=y_i - a(x_i) - \epsilon;\\$

Объекты 2-5 называются опорными и учитываются при определении вектора весов. На объектах 1-3 потери равны нулю, а на 4 и 5 потери больше нуля. Уравнение регрессии выражается через двойственные переменные: $a(x)=\sum_{i=1}^l (\lambda_i^- - \lambda_i^+)K(x_i,x)-w0;$ , где параметр $w_0$ определяется из уравнений

$(w,x_i)-w_0 = \begin{cases} y+\epsilon, & \mbox{ } \x_i \mbox{ belongs to 2nd type }\\ y-\epsilon, & \mbox{ } \x_i \mbox{ belongs to 3rd type }\\ \end{cases}$

Параметр $w_0$ можно определить из любого уравнения, но чтобы избежать вычислительных ошибок берется медиана полученного множества для $w_0$ .

Как уже упоминалось, параметр $\epsilon$ задает эксперт, а параметр С подбирается по скользящему контролю, что является трудоёмкой процедурой.

Мультиклассовый метод опорных векторов

В случае нескольких классов на практике зачастую применяется решающее правило, основанное на разбиении задачи на бинарные по схеме "один против остальных" (One-vs-Rest):

$f(x) = \arg \max_{y\in Y} (\langle w_y, x \rangle + b_y).$

Стоит отметить, что дальнейшее обобщение такого решающего правила приводит к методу опорных векторов со структурированным результатом (Structured Output SVM).

Для обучения параметров $w_0, b_0, \dots, w_K, b_K$ такой композиции алгоритмов может быть решено $K$ стандартных для метода опорных векторов задач оптимизации, однако данный подход имеет свои недостатки. В работе Краммера и Зингера была предложена следующая совместная формулировка задачи оптимизации

$\min_{w,\xi} \frac{1}{2} ||w_y||^2 + C \sum_{i} \xi_i,$

при ограничениях $\langle w_{y_i}, x_i \rangle - \langle w_{y}, x_i \rangle \geq 1 - \delta_{y_i, y} - \xi_i$ , задающих ответы классификатора на обучающей выборке и ограничениях положительности штрафов $\xi_i \geq 0$ .

Двойственная задача такой формулировки имеет вид

$\min_{\alpha} \frac{1}{2} \sum_{y\in Y} \sum_{i} \sum_{j} \alpha_i^y \alpha_j^y \langle x_i, x_j \rangle + \sum_{y \in Y} \sum_{i} (1-\delta_{y_i, y} ) \alpha_i^y$

при неотрицательных коэффициентах $\alpha_i^y \geq 0$ .

Программные реализации

SVMLight

Наиболее развитая и популярная реализация SVM на С++. Библиотека адаптирована для больших выборок и имеет эффективную реализацию скользящего контроля. Включены стандартные ядерные функции и допускается использование предварительно вычисленных матриц ядерных функций.

LIBSVM и LIBLINEAR

Эффективные и простые в использовании реализации SVM на С++ со схожими интерфейсами. В LibLinear реализована только линейная классификация и регрессия. Работают с большими выборками.

Литература

Вапник В. Н. Восстановление зависимостей по эмпирическим данным. — М.: Наука, 1979. — 448 с. (подробнее)
Hastie, T., Tibshirani, R., Friedman, J. The Elements of Statistical Learning, 2nd edition. — Springer, 2009. — 533 p. (подробнее)

Ссылки

SMO — Sequential Minimal Optimization — эффективный алгоритм настройки SVM.
Джон Платт — сайт автора SMO: статьи, реализации и тестовые примеры.
Линейный классификатор
Машинное обучение (курс лекций, К.В.Воронцов)
Alexey Nefedov. Support Vector Machines: A Simple Tutorial

Источник — «http://www.machinelearning.ru/wiki/index.php?title=%D0%9C%D0%B0%D1%88%D0%B8%D0%BD%D0%B0_%D0%BE%D0%BF%D0%BE%D1%80%D0%BD%D1%8B%D1%85_%D0%B2%D0%B5%D0%BA%D1%82%D0%BE%D1%80%D0%BE%D0%B2»

Категории: Классификация | Энциклопедия анализа данных | Линейные классификаторы