Графические модели (курс лекций)/2013/Задание 3
Материал из MachineLearning.
|
Начало выполнения задания: 1 апреля 2013 г.;
Срок сдачи: 11 апреля 2013 г. (четверг), 23:59.
Среда для выполнения задания — MATLAB. Неэффективная реализация кода может негативно отразиться на оценке.
Модель авторегрессии
Случайный процесс с дискретным временем ,
называется авторегрессией первого порядка, если
.
Здесь — параметр сдвига,
— авторегрессионная матрица,
— матрица ковариации шума, шумовые компоненты
предполагаются независимыми. Процесс авторегрессии является стационарным (в широком смысле), если все собственные значения матрицы
(включая комплексные) по модулю меньше единицы. Мат.ожидание
стационарного процесса авторегрессии определяется как
,
где — единичная матрица размера
.
В терминах графических моделей авторегрессия первого порядка представляет собой байесовскую сеть с графом вида цепочка (см. рис.), где совместное распределение задается как
,
а — начальная предыстория.
Авторегрессия M-го порядка задается как
.
Здесь шумовые компоненты по-прежнему предполагаются независимыми. Авторегрессия M-го порядка может быть сведена к авторегрессии первого порядка как
Поэтому авторегрессия M-го порядка является стационарной, когда все собственные значения матрицы по модулю меньше единицы. В частности, для случая
условие стационарности эквивалентно
, а для случая
— условию
. Мат.ожидание стационарной регрессии M-го порядка определяется как
.
В дальнейшем для удобства набор матриц будем обозначать через
.
В терминах графических моделей авторегрессия M-го порядка представляет собой байесовскую сеть с графом, показанном на рис. справа, где совместное распределение задается как
,
а — начальная предыстория.
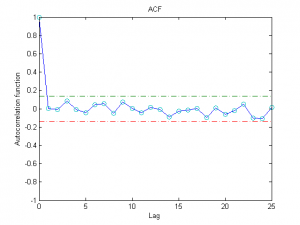
Одним из способов определения адекватности моделирования данных с помощью модели авторегрессии является исследование остатков
,
где — оценки параметров авторегрессии (например, оценки максимального правдоподобия). Для успешного объяснения данных с помощью авторегрессии необходимо, чтобы остатки не были коррелированы по времени. Другими словами, выборочная автокорреляционная функция
должна лежать в интервале для всех
. Здесь через
обозначена
-квантиль одномерного нормального распределения. Для уровня значимости
соответствующая квантиль равна 1.96.
Авторегрессионная скрытая марковская модель
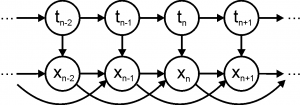
Авторегрессионная скрытая марковская модель M-го порядка — это байесовская сеть, граф которой показан на рис. справа, а совместное распределение задается как
.
Здесь — скрытые дискретные состояния,
— непрерывные наблюдаемые переменные. Априорное распределение
задается вектором
, причем все
и
. Распределение
задается матрицей перехода
размера
, где в
-ой позиции стоит вероятность перехода из состояния
в состояние
. Все элементы этой матрицы неотрицательны, а сумма элементов по каждой строке равна единице. Модель генерации данных соответствует модели авторегрессии, в которой параметры
зависят от текущего состояния
. Таким образом,
.
В результате полный набор параметров модели состоит из
. Глубина авторегрессии
, количество скрытых состояний
, а также начальная предыстория
задаются пользователем.
Формулировка задания
- Для модели авторегрессии M-го порядка:
- Вывести формулы для оценки параметров модели
по наблюдениям
с помощью метода максимального правдоподобия;
- Реализовать процедуру генерации сигнала из модели авторегрессии;
- Реализовать процедуру оценки параметров
по методу максимального правдоподобия;
- Вывести формулы для оценки параметров модели
- Провести эксперименты с авторегрессией M-го порядка:
- Сгенерировать данные из модели авторегрессии, а затем восстановить параметры по методу максимального правдоподобия (рассмотреть различные значения параметров модели, а также различные размерности параметров). Как ведут себя значение правдоподобия, авторегрессионные остатки и восстановленные параметры при глубине авторегрессии меньше истинного значения, равного истинному значению и больше истинного значения? Какой объем данных необходим для адекватного восстановления параметров модели?
- Сгенерировать данные из модели случайного процесса, отличного от авторегрессии. К чему приводит попытка объяснения таких данных с помощью авторегрессии?
- Для авторегрессионной скрытой марковской модели:
- Вывести формулы ЕМ-алгоритма для оценки параметров модели
, при этом предусмотреть ситуации, когда часть параметров задается пользователем;
- Реализовать процедуру генерации сигнала из модели;
- Реализовать процедуру вычисления маргинальных распределений для отдельных скрытых переменных
и пар соседних переменных
при известных наблюдениях и параметрах модели с помощью алгоритма «вперёд-назад»;
- Реализовать процедуру оценки параметров модели по методу максимального правдоподобия с помощью EM-алгоритма;
- Реализовать процедуру поиска наиболее вероятной конфигурации скрытых переменных по наблюдаемым данным и параметрам модели с помощью алгоритма Витерби;
- Вывести формулы ЕМ-алгоритма для оценки параметров модели
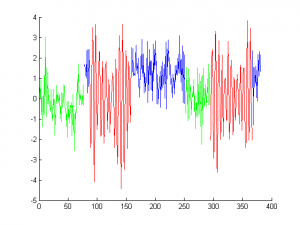
- Провести эксперименты с авторегрессионной скрытой марковской моделью:
- Сгенерировать наблюдаемые и скрытые переменные из модели, а затем восстановить скрытые компоненты с помощью алгоритма Витерби при истинных параметрах модели, а также путем взятия аргмаксимумов для маргинальных распределений на
. Рассмотреть ситуации хорошо отделимых и слабо отделимых состояний, а также различные размерности параметров модели. Привести пример ситуации, когда алгоритм Витерби и аргмаксимумы маргиналов приводят к существенно различным конфигурациям.
- Сгенерировать наблюдаемые и скрытые переменные из модели, а затем восстановить параметры модели только по наблюдаемым данным с помощью ЕМ-алгоритма. Рассмотреть различные ситуации. Имеет ли смысл в ЕМ-алгоритме задавать часть параметров модели вручную? Как параметры, задаваемые вручную, влияют на значение правдоподобия и на качество сегментации сигнала?
- Сгенерировать наблюдаемые и скрытые переменные из модели, а затем восстановить скрытые компоненты с помощью алгоритма Витерби при истинных параметрах модели, а также путем взятия аргмаксимумов для маргинальных распределений на
- [Бонус] Предложить свою схему сегментации подмножества сигналов, сгенерированных из авторегрессионной скрытой марковской модели, без использования модели авторегрессии.
- Составить отчёт в формате PDF с описанием всех проведённых исследований. Данный отчёт должен включать в себя вывод необходимых формул, различные графики с результатами экспериментов, а также развернутые комментарии к полученным результатам.
Рекомендации по выполнению задания
1. Вывод формул для авторегрессии и авторегрессионной скрытой марковской модели удобно осуществлять путем введения обозначений
.
Тогда выражение можно лаконично записать как
.
После вывода необходимых формул рекомендуется убедиться в том, что эти формулы переходят в стандартные формулы для оценки параметров многомерного нормального распределения (в том числе в рамках скрытой марковской модели) при обнулении всех A.
В случае вывода формул для при известном
или, наоборот, формул для
при фиксированном
нотация через
не подходит.
2. При тестировании ЕМ-алгоритма рекомендуется отслеживать монотонное возрастание логарифма неполного правдоподобия в итерациях. При этом вблизи локального максимума правдоподобия возможны небольшие нарушения монотонности из-за вычислительных погрешностей.
3. Обратите внимание, что для возможности реализации в сигналах сегментов типа некоторой длины
необходимо, чтобы величина
была существенно отлична от нуля.
Оформление задания
Выполненное задание следует отправить письмом по адресу bayesml@gmail.com с заголовком письма «[ГМ13] Задание 3 <ФИО>». Убедительная просьба присылать выполненное задание только один раз с окончательным вариантом. Также убедительная просьба строго придерживаться заданных ниже прототипов реализуемых функций.
Присланный вариант задания должен содержать в себе:
- Файл отчёта в формате PDF с указанием ФИО;
- Все исходные коды с необходимыми комментариями.
| Генерация выборки из модели авторегрессии | |||||
|---|---|---|---|---|---|
| X = ar_generate(N, w, A, Sigma, X0) | |||||
| ВХОД | |||||
| |||||
| ВЫХОД | |||||
|
Если начальная предыстория не задана, то
выбирается равной мат.ожиданию процесса авторегрессии.
| Оценка параметров авторегрессии | |||||
|---|---|---|---|---|---|
| [w, A, Sigma, res, logLH] = ar_fit(X, M) | |||||
| ВХОД | |||||
| |||||
| ВЫХОД | |||||
|
| Генерация выборки из авторегрессионной скрытой марковской модели | |||||||
|---|---|---|---|---|---|---|---|
| [X, T] = arhmm_generate(N, p, R, W, A, Sigmas, X0) | |||||||
| ВХОД | |||||||
| |||||||
| ВЫХОД | |||||||
|
Если начальная предыстория не задана, то
выбирается равной мат.ожиданию процесса авторегрессии, соответствующего сгенерированному состоянию
.
| Оценка маргиналов на скрытые переменные | ||||||
|---|---|---|---|---|---|---|
| [gamma, ksi, logLH] = arhmm_posterior(X, p, R, W, A, Sigmas) | ||||||
| ВХОД | ||||||
| ||||||
| ВЫХОД | ||||||
|
| Оценка параметров авторегрессионной скрытой марковской модели с помощью ЕМ-алгоритма | ||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [p, R, W, A, Sigmas, logLH] = arhmm_fit(X, K, M, param_name1, param_value1, ...) | ||||||||||||||||||||||||||||||||||||
| ВХОД | ||||||||||||||||||||||||||||||||||||
|