Критерий Бройша-Пагана

Материал из MachineLearning.

(Различия между версиями)

Версия 22:16, 27 декабря 2013

Критерий Бройша-Пагана (также Бреуша-Пагана, англ. Breusch-Pagan test) — один из статистических тестов для проверки наличия гетероскедастичности (то есть непостоянной дисперсии) случайных ошибок модели линейной регрессии. Применяется, если есть основания полагать, что дисперсия ошибок $\sigma_t$ может зависеть от некоторой совокупности наблюдаемых переменных:

$\sigma_t^2 = z_t^T \gamma, \;t = 1,\dots,n,$

где $z_t = (1,z_{2t},\dots,z_{pt})^T.$

Определение

Формулировки проверяемой и альтернативной гипотез выглядят следующим образом:

$H_0: \quad \gamma_2 = \ldots = \gamma_p = 0 \quad \Leftrightarrow \quad \sigma_1^2 = \ldots = \sigma_n^2 \quad \Leftrightarrow$ остатки гомоскедастичны;

$H_1: \quad H_0$ неверна.

Статистика критерия может быть получена на основе метода множителей Лагранжа и имеет следующий вид:

$LM=\left (\frac{\partial l}{\partial\theta} \right )'\left (-E\left [\frac{\partial^2 l}{\partial\theta \partial\theta'} \right ] \right )^{-1}\left(\frac{\partial l}{\partial\theta} \right )$ .

Вычисление статистики сводится к следующей процедуре^[1].

Шаг 1: Исходная модель $y = X\beta+\varepsilon$ оценивается обычным методом наименьших квадратов, вычисляются остатки $\varepsilon_t$ .
Шаг 2: Дисперсия ошибки модели (в предположении её гомоскедастичности) оценивается как $\hat{\sigma}^2 = \frac{1}{n} RSS$ .
Шаг 3: Вычисляются стандартизированные остатки $\frac{\varepsilon^2}{\hat{\sigma}^2}$ .
Шаг 4: Строится дополнительная регрессия квадратов стандартизированных ошибок на исходные наблюдаемые переменные:

$\varepsilon_t^2=\gamma_1+\gamma_2z_{2t}+\dots+\gamma_pz_{pt}+\eta_t$ .

Шаг 5: $LM=n R^{2}$ , где $R^{2}$ — коэффициент детерминации построенной на предыдущем шаге регрессии.

При справедливости нулевой гипотезы о гомоскедастичности остатков статистика критерия имеет распределение хи-квадрат с $p-1$ степенями свободы.

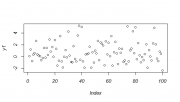
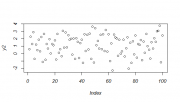
Пример

Рассмотрим пример с использованием системы R:

> ## моделируем наблюдаемые переменные
> x <- rep(c(-1,1), 50)
> ## генерируем гетероскедастичные ошибки
> err1 <- rnorm(100, sd=rep(c(1,2), 50))
> ## генерируем гомоскедастичные ошибки
> err2 <- rnorm(100)
> ## генерируем отклик
> y1 <- 1 + x + err1
> y2 <- 1 + x + err2
> ## проводим тест Бройша-Пагана
> bptest(y1 ~ x)$p.value
          BP 
0.0007141008  
> bptest(y2 ~ x)$p.value
       BP
0.9464273

Реализации

MatLab: встроенной реализации нет, есть реализации на File Exchange.
R: функция bptest в стандартном пакете lmtest и ncvtest в пакете car.

Ссылки

Breusch T.S., Pagan A.R. (1979). "Simple test for heteroscedasticity and random coefficient variation". Econometrica, 47(5), 1287-1294.
EnWiki: Breusch–Pagan test
Магнус Я.Р., Катышев П.К., Пересецкий А.А. (2007) "Эконометрика. Начальный курс". М.:Дело, стр. 179-183.
YouTube: The Breusch Pagan test for heteroscedasticity

Примечания

Источник — «http://www.machinelearning.ru/wiki/index.php?title=%D0%9A%D1%80%D0%B8%D1%82%D0%B5%D1%80%D0%B8%D0%B9_%D0%91%D1%80%D0%BE%D0%B9%D1%88%D0%B0-%D0%9F%D0%B0%D0%B3%D0%B0%D0%BD%D0%B0»

Категории: Линейная регрессия | Регрессионный анализ

@@ Строка 1: / Строка 1: @@
+'''Критерий Бройша-Пагана''' (также ''Бреуша-Пагана'', англ. ''Breusch-Pagan test'') — один из статистических тестов для проверки наличия гетероскедастичности (то есть непостоянной дисперсии) случайных ошибок модели [[Регрессионный анализ|линейной регрессии]]. Применяется, если есть основания полагать, что дисперсия ошибок <tex>\sigma_t</tex> может зависеть от некоторой совокупности наблюдаемых переменных:
+::<tex>\sigma_t^2 = z_t^T \gamma, \;t = 1,\dots,n,</tex>
+где <tex>z_t = (1,z_{2t},\dots,z_{pt})^T.</tex>
 ==Определение==
-'''Критерий Бройша-Пагана''' (также ''Бреуша-Пагана'', англ. ''Breusch-Pagan test'') - один из статистических тестов для проверки наличия гетероскедастичности (то есть непостоянной дисперсии) случайных ошибок модели линейной регрессии. Применяется, если есть основания полагать, что дисперсия случайных ошибок может зависеть от некоторой совокупности переменных. В данном случае проверяется линейная зависимость дисперсии случайных ошибок <tex> \sigma_t </tex> от наблюдаемых переменных:
-::<tex>\sigma_t^2 = z_t^T \gamma, \quad t = 1,\dots,n</tex>, где <tex>z_t = (1,z_{2t},\dots,z_{pt})^T</tex>.
 Формулировки проверяемой и альтернативной гипотез выглядят следующим образом:
@@ Строка 11: / Строка 10: @@
 ::<tex>H_1: \quad H_0</tex> неверна.
-==Процедура теста==
+Статистика критерия может быть получена на основе метода множителей Лагранжа и имеет следующий вид:
-Следуя методу множителей Лагранжа, получаем следующий вид статистики теста:
+::<tex>LM=\left (\frac{\partial l}{\partial\theta} \right )'\left (-E\left [\frac{\partial^2 l}{\partial\theta \partial\theta'} \right ] \right )^{-1}\left(\frac{\partial l}{\partial\theta} \right )</tex>.
-:<tex>LM=\left (\frac{\partial l}{\partial\theta} \right )'\left (-E\left [\frac{\partial^2 l}{\partial\theta \partial\theta'} \right ] \right )^{-1}\left(\frac{\partial l}{\partial\theta} \right )</tex>.
+Вычисление статистики сводится к следующей процедуре<ref name="heij">C. Heij, P. de Boer (2004). [https://akela.mendelu.cz/~xhavir3/ekm/Heij.pdf "Econometric Methods with Applications in Business and Economics"]. Oxford University Press, pp. 344–345.</ref>.
+* ''Шаг 1'': Исходная модель <tex> y = X\beta+\varepsilon</tex> оценивается обычным [[Метод наименьших квадратов|методом наименьших квадратов]], вычисляются остатки <tex>\varepsilon_t</tex>.
+* ''Шаг 2'': Дисперсия ошибки модели (в предположении её гомоскедастичности) оценивается как <tex>\hat{\sigma}^2 = \frac{1}{n} RSS</tex>.
+* ''Шаг 3'': Вычисляются стандартизированные остатки <tex>\frac{\varepsilon^2}{\hat{\sigma}^2} </tex>.
+* ''Шаг 4'': Строится дополнительная регрессия квадратов стандартизированных ошибок на исходные наблюдаемые переменные:
+::<tex> \varepsilon_t^2=\gamma_1+\gamma_2z_{2t}+\dots+\gamma_pz_{pt}+\eta_t </tex>.
+* ''Шаг 5'': <tex> LM=n R^{2}</tex>, где <tex>R^{2}</tex> — [[коэффициент детерминации]] построенной на предыдущем шаге регрессии.
-В учебнике [C. Heij, P. de Boer, 2004] говорится о том что подсчет статистики сводится к следующей процедуре:
+При справедливости нулевой гипотезы о гомоскедастичности остатков статистика критерия имеет распределение хи-квадрат с <tex>p-1</tex> степенями свободы.
-* ''Шаг 1'': Исходная модель <tex> y = X\beta+\varepsilon</tex> оценивается обычным МНК, вычисляются остатки <tex>\varepsilon_t</tex>;
-* ''Шаг 2'': Вычисление оценки дисперсии остатков (в предположении их гомоскедастичности):
-:<tex>\hat{\sigma}^2 = \frac{1}{n} RSS</tex>;
-* ''Шаг 3'': Вычисление стандартизированных остатков <tex>\frac{\varepsilon^2}{\hat{\sigma}^2} </tex>;
-* ''Шаг 4'': Построение дополнительной регрессии квадратов стандартизированных ошибок на исходные наблюдаемые переменные
-:<tex> \varepsilon_t^2=\gamma_1+\gamma_2z_{2t}+\dots+\gamma_pz_{pt}+\eta_t </tex>;
-* ''Шаг 5'': <tex> LM=n R^{2}</tex>, где <tex>R^{2}</tex> - коэффициент детерминации построенной на предыдущем шаге регрессии.
-В работе [Breush, Pagan, 1979] установлено, что при справедливости нулевой гипотезы о гомоскедастичности остатков статистика теста имеет распределение хи-квадрат с p-1 степенями свободы <tex> LM \sim \chi^2 \left (p - 1 \right )</tex>.
 ==Пример==
@@ Строка 62: / Строка 56: @@
 == Ссылки ==
-* Breusch T.S., Pagan A.R. (1979). [https://www.aae.wisc.edu/aae637/handouts/breusch_pagan_hetero_test_article.pdf "Simple test for heteroscedasticity and random coefficient variation"].
+* Breusch T.S., Pagan A.R. (1979). [https://www.aae.wisc.edu/aae637/handouts/breusch_pagan_hetero_test_article.pdf "Simple test for heteroscedasticity and random coefficient variation"]. Econometrica, 47(5), 1287-1294.
 * [http://en.wikipedia.org/wiki/Breusch%E2%80%93Pagan_test EnWiki: Breusch–Pagan test]
-* C. Heij, P. de Boer (2004). [https://akela.mendelu.cz/~xhavir3/ekm/Heij.pdf "Econometric Methods with Applications in Business and Economics"]. Oxford University Press, pp. 344–345.
 * Магнус Я.Р., Катышев П.К., Пересецкий А.А. (2007) [http://math.isu.ru/ru/chairs/me/files/books/magnus.pdf "Эконометрика. Начальный курс"]. М.:Дело, стр. 179-183.
 * [http://www.youtube.com/watch?v=wzLADO24CDk YouTube: The Breusch Pagan test for heteroscedasticity]
+== Примечания ==
+<references />
+[[Категория:Линейная регрессия]]
+[[Категория:Регрессионный анализ]]

Критерий Бройша-Пагана

Материал из MachineLearning.

Версия 22:16, 27 декабря 2013

Содержание

Определение

Пример

Реализации

Ссылки

Примечания

Просмотры

Личные инструменты

Навигация

Поиск

Инструменты