Марковский алгоритм кластеризации
Материал из MachineLearning.
(→Марковский алгоритм кластеризации) |
|||
| Строка 47: | Строка 47: | ||
| - | 1) распространение - представляет | + | 1) распространение (N) - представляет собой возведение матрицы в степень N. Данная операция усиливает поток из вершины на потенциальных участников кластера. |
| - | 2) накачивание - представляет собой | + | 2) накачивание (K) - представляет собой применение произведения Адамара матрицы самой на себя. (произведение Адамара - бинарная операция над двумя матрицами одинаковой размерности, результатом которой является матрица той же размерности, в которой каждый элемент с индексами i, j — это произведение элементов с индексами i, j исходных матриц). Данная операция уменьшает вероятности переходов между кластерами быстрее чем вероятности переходов внутри одного кластера. Так же на этом шаге выполняеца нормирование каждого столбца матрицы. |
| - | + | ||
| + | |||
| + | В данном алгоритме необходимо подбирать степь распространения и накачивании (так как это непосредственно вляйет на разбиение). Увеличение степени распространении - увеличивает средний размер кластера, в то время как увеличение степени накачивания - приводит к увеличению количества кластеров. | ||
| + | |||
| + | В ходе выполнения алгоритма выделяются узлы которые являются "центрами" кластеров. Наглядная визуализация алгоритма приведена на рисунки 3. Как можно заметить в ходе работы алгоритма граф становится все менее и менее связным пока не будет разделен на кластеры. | ||
| - | |||
| Строка 58: | Строка 61: | ||
---- | ---- | ||
| + | ==== Примеры способов кластеризации ==== | ||
| - | |||
[[Изображение:MCL1.jpeg|200px|thumb| Рисунок 4 кластеризации простого графа методом MCL. Слева грав до кластеризации, справо после кластеризации]] | [[Изображение:MCL1.jpeg|200px|thumb| Рисунок 4 кластеризации простого графа методом MCL. Слева грав до кластеризации, справо после кластеризации]] | ||
| Строка 66: | Строка 69: | ||
Расмотрим работу данного метода на примере кластеризации простого графа и его смежной матрицы. | Расмотрим работу данного метода на примере кластеризации простого графа и его смежной матрицы. | ||
| - | Возьмем граф состоящий из 12 вершин и составим для него матрицу вероятностей переходов между узлами. Так как граф является не взвешенным вероятности перехода между соседними узлами и вероятность остаться в этом узле будет равна 1/(количество ребер смежных с вершиной + 1). Матрица вероятностей переходов между узлами представленна на рисунке 5. | + | Возьмем граф состоящий из 12 вершин и составим для него матрицу вероятностей переходов между узлами. Так как граф является не взвешенным вероятности перехода между соседними узлами и вероятность остаться в этом узле будет равна 1/(количество ребер смежных с вершиной + 1). Матрица вероятностей переходов между узлами представленна вверху рисунка 5. Кроме этого на рисунке 5 представлен результат выполнения функции распространения без регулярной инфляции. Как не сложно заметить в результате этого получается полносвязный граф. Однако при выполнении инфляции в каждом цикле алгоритма приводит к выделению кластерной структуры алгоритма, это можно наблюдать на рисунке 6. |
| - | + | ||
| - | + | ||
| - | + | ||
[[Изображение:MCL2.png|200px|thumb| Рисунок 5 экспансия без инфляции]] | [[Изображение:MCL2.png|200px|thumb| Рисунок 5 экспансия без инфляции]] | ||
| Строка 75: | Строка 75: | ||
| - | [[Изображение:MCL3.jpeg|200px|thumb| Рисунок | + | [[Изображение:MCL3.jpeg|200px|thumb| Рисунок 6 экспансия с инфляцией]] |
---- | ---- | ||
| + | ==== Плюсы и минусы алгоритма ==== | ||
| - | + | ||
#Плюсы алгоритма | #Плюсы алгоритма | ||
##Работает как с взвешенными, так и с невзвешенными графами | ##Работает как с взвешенными, так и с невзвешенными графами | ||
| Строка 88: | Строка 89: | ||
##Не подходит для кластеров большого размера | ##Не подходит для кластеров большого размера | ||
##Часто кластеры получаются разного размера | ##Часто кластеры получаются разного размера | ||
| - | ##Время работы алгоритма в наихудшем случае Ο(V^3) | + | ##Время работы алгоритма в наихудшем случае Ο(V^3), однаков слкчае разряженной матрицы время расчета |
| - | + | может уменьшаться до Ο(V) и расчет может быть распаралален на несколько процессоров. | |
| Строка 97: | Строка 98: | ||
[Satuluri V. M. Scalable clustering of modern networks : дис. – The Ohio State University, 2012.] | [Satuluri V. M. Scalable clustering of modern networks : дис. – The Ohio State University, 2012.] | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| Строка 119: | Строка 107: | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
#На сегодняшний день данный алгоритм применяется для данных в молекулярной биологии (выделение групп генов) [S. Brohee and J. van Helden. Evaluation of clustering algorithms for protein- | #На сегодняшний день данный алгоритм применяется для данных в молекулярной биологии (выделение групп генов) [S. Brohee and J. van Helden. Evaluation of clustering algorithms for protein- | ||
protein interaction networks. BMC Bioinformatics, 7, 2006.][J. Vlasblom and S.J. Wodak. Markov clustering versus affinity propagation for the partitioning of protein interaction graphs. BMC bioinformatics, 10(1):99, 2009.] | protein interaction networks. BMC Bioinformatics, 7, 2006.][J. Vlasblom and S.J. Wodak. Markov clustering versus affinity propagation for the partitioning of protein interaction graphs. BMC bioinformatics, 10(1):99, 2009.] | ||
Версия 19:07, 12 декабря 2018
| | Данная статья является непроверенным учебным заданием.
До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru. По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}. См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе. |
Содержание |
Марковский алгоритм кластеризации
Марковский алгоритм кластеризации (MCL, Markov Clustering Algorithm) — алкоритм кластерного анализа основанный на потоке (случайном блуждании) в графе. Изначально разработан для выделения кластеров в простом графе, однако может быть применен к любым объектам для которых задана матрица сходства/различия. Данный алгоритм является быстрый и масштабируемым алгоритмо кластеризации.
Термины и определения
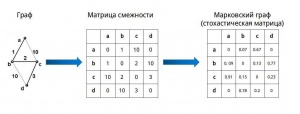
Граф состоит из двух типов объектов 1) вершин(узлов)- V 2)ребер (пар вершин соединенных между собой) - E. Формально это можно записать как G:=(V,E) Кроме этого, каждый граф можно представить в виде матрицы смежности (M) размером V*V. Где Mij равен растоянию между узлом i и узлом j.
Случайный обход графа - такой обход вершин граф, при котором выбор следующей вершины зависит только от текущего положения на графе, а вероятность перейти к любой вершинне расчитывется исходя из матрицы смежности. Следует отметить что при таком обходе одна вершина может быть посещена неограниченное число раз. Случайное блуждание в графе - это цепь Маркова.
Строго определить что такое кластер в графе, не представляется возможном, однако можно дать два близких определения:
- Длинна пути между узлами одного кластера мало по сравнению с длинно пути между точками пренадлежажащими
одному кластеру.
- При случайном обходе графа, прежде чем покинуть кластер будут посещены многоие из его вершин
Общее описание метода
Метод опирается на следующе допущение - расстояния между узлами графа относящихся к одному кластеру, меньше чем растояние между узлами относящимся к различным кластерам. т.е. верояность перехода (поток) между узлами внутри одного кластера много больше чем между узлами относящимися к разным кластерам. Таким образом если усиливать поток там где он силен и ослаблять его там где он слаб то согласно парадигме кластеризации графа границы между различными кластерами будут исчезать. Таким образом будет выявлена кластерная структура графа.
Моделирование потока в графе осуществляется путем преобразования его в марковский граф (см. рисуйнок 1).
На первом шаге граф преобразуется в матрицу растояний между узлами (смежную матрицу). В слуае если граф является не взвешенным можно считать что вес всех ребер равен единице. На втором шаге происходит преобразование смежной матрицы в матрицу вероятностей переходов между узлами (стохастическую матрицу). Для этого как правило нормируют значения в каждом отдельном столбце матрицы рассотяний, однако может быть применен любой другой алгоритм.
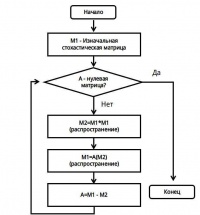
После того как стохастическую матрица получена, к ней поочердно применяют две функции (распространение и накачивание) до тех пор пока матрица изменяется (см. рисуйнок 2).
1) распространение (N) - представляет собой возведение матрицы в степень N. Данная операция усиливает поток из вершины на потенциальных участников кластера.
2) накачивание (K) - представляет собой применение произведения Адамара матрицы самой на себя. (произведение Адамара - бинарная операция над двумя матрицами одинаковой размерности, результатом которой является матрица той же размерности, в которой каждый элемент с индексами i, j — это произведение элементов с индексами i, j исходных матриц). Данная операция уменьшает вероятности переходов между кластерами быстрее чем вероятности переходов внутри одного кластера. Так же на этом шаге выполняеца нормирование каждого столбца матрицы.
В данном алгоритме необходимо подбирать степь распространения и накачивании (так как это непосредственно вляйет на разбиение). Увеличение степени распространении - увеличивает средний размер кластера, в то время как увеличение степени накачивания - приводит к увеличению количества кластеров.
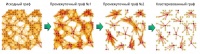
В ходе выполнения алгоритма выделяются узлы которые являются "центрами" кластеров. Наглядная визуализация алгоритма приведена на рисунки 3. Как можно заметить в ходе работы алгоритма граф становится все менее и менее связным пока не будет разделен на кластеры.
Примеры способов кластеризации
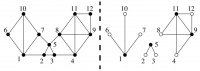
Расмотрим работу данного метода на примере кластеризации простого графа и его смежной матрицы.
Возьмем граф состоящий из 12 вершин и составим для него матрицу вероятностей переходов между узлами. Так как граф является не взвешенным вероятности перехода между соседними узлами и вероятность остаться в этом узле будет равна 1/(количество ребер смежных с вершиной + 1). Матрица вероятностей переходов между узлами представленна вверху рисунка 5. Кроме этого на рисунке 5 представлен результат выполнения функции распространения без регулярной инфляции. Как не сложно заметить в результате этого получается полносвязный граф. Однако при выполнении инфляции в каждом цикле алгоритма приводит к выделению кластерной структуры алгоритма, это можно наблюдать на рисунке 6.
Плюсы и минусы алгоритма
- Плюсы алгоритма
- Работает как с взвешенными, так и с невзвешенными графами
- Устойчив к шуму в данных
- Количество кластеров не указано заранее, но можно настроить степень детализации кластера
- Может находить кластера произвольной формы
- Минусы алгоритма
- Не нацелен находить перекрывающиеся кластеры (*)
- Не подходит для кластеров большого размера
- Часто кластеры получаются разного размера
- Время работы алгоритма в наихудшем случае Ο(V^3), однаков слкчае разряженной матрицы время расчета
может уменьшаться до Ο(V) и расчет может быть распаралален на несколько процессоров.
Данный алгоритм был разработан в рамках PhD работы Van Dongen в 2000 году в центре математических и компьютерных наук в Нидерландах. В 2012 году были разработанны такие вариации алгоритма как MLR-MCL и R-MCL которые облдали меньшим количеством недостатков. [Satuluri V. M. Scalable clustering of modern networks : дис. – The Ohio State University, 2012.]
Графы часто возникают при упрощении сложных систем. К примеру в виде графа удобно отображать:
- взамосвязи различных сайтов в интернете
- Социальные сети (сети контактов)
- Генные сети в молекулярной биологии
- порты, аэропорты, города (в качестве узлов графа)и пути их соединяюющие (в качестве ребер).
- На сегодняшний день данный алгоритм применяется для данных в молекулярной биологии (выделение групп генов) [S. Brohee and J. van Helden. Evaluation of clustering algorithms for protein-
protein interaction networks. BMC Bioinformatics, 7, 2006.][J. Vlasblom and S.J. Wodak. Markov clustering versus affinity propagation for the partitioning of protein interaction graphs. BMC bioinformatics, 10(1):99, 2009.]
- анилизе изображений.
Список используемой литературы
1) Van Dongen, S. 2000. “Graph clustering by flow simulation.” Ph.D. thesis, University of Utrecht, The Netherlands
2) https://www.micans.org/mcl/index.html
3) Li, Li, Christian J. Stoeckert, and David S. Roos. "OrthoMCL: identification of ortholog groups for eukaryotic genomes." Genome research 13.9 (2003): 2178-2189.
4)Satuluri, Venu, Srinivasan Parthasarathy, and Duygu Ucar. "Markov clustering of protein interaction networks with improved balance and scalability." Proceedings of the first ACM international conference on bioinformatics and computational biology. ACM, 2010.