Методы оптимизации в машинном обучении (курс лекций)/2012/Задание 3
Материал из MachineLearning.
(релиз) |
|||
| (8 промежуточных версий не показаны.) | |||
| Строка 1: | Строка 1: | ||
| - | |||
| - | |||
__NOTOC__ | __NOTOC__ | ||
| Строка 7: | Строка 5: | ||
[[Image:MOMO12_IPM.png|300px]] | [[Image:MOMO12_IPM.png|300px]] | ||
| - | '''Начало выполнения задания''': | + | '''Начало выполнения задания''': 23 ноября 2012 |
| - | '''Срок сдачи''': {{ins| | + | '''Срок сдачи''': {{ins|6 декабря 2012 (четверг), 23:59}} |
Среда реализации задания – MATLAB. | Среда реализации задания – MATLAB. | ||
=== Модель <tex>L_1</tex>-регуляризованной линейной регрессии === | === Модель <tex>L_1</tex>-регуляризованной линейной регрессии === | ||
| + | |||
| + | ==== Формулировка метода ==== | ||
| + | |||
| + | Рассматривается задача восстановления регрессии. Имеется обучающая выборка <tex>\{\vec{x}_n,t_n\}_{n=1}^N</tex>, где <tex>\vec{x}_n\in\mathbb{R}^D</tex> — вектор признаков для объекта <tex>n</tex>, а <tex>t_n\in\mathbb{R}</tex> — его регрессионное значение. Задача заключается в прогнозировании регрессионного значения <tex>t_{new}</tex> для нового объекта, представленного своим вектором признаков <tex>\vec{x}_{new}</tex>. | ||
| + | |||
| + | В линейной регрессии прогнозирование осуществляется с помощью линейной функции: | ||
| + | |||
| + | <tex>t(\vec{x}_{new}) = \sum_{d=1}^Dw_dx_{new,d} = \vec{w}^T\vec{x}_{new}</tex>, | ||
| + | |||
| + | где <tex>\vec{w}\in\mathbb{R}^D</tex> — некоторые веса. Настройка весов осуществляется путем минимизации следующего регуляризованного критерия: | ||
| + | |||
| + | <tex>J = \frac{1}{2}\sum_{n=1}^N(t_n - \vec{w}^T\vec{x}_n)^2 + \lambda\sum_{d=1}^D|w_d| = \frac{1}{2}||\vec{t} - X\vec{w}||^2 + \lambda||\vec{w}||_1\rightarrow\min_{\vec{w}}.\qquad (1)</tex> | ||
| + | |||
| + | Здесь <tex>\lambda\ge 0</tex> — задаваемый пользователем параметр регуляризации. Использование <tex>L_1</tex>-регуляризации позволяет, во-первых, снизить вероятность переобучения алгоритма, а во-вторых, получить т.н. разреженное решение. В разреженном решении часть компонент оптимального вектора весов <tex>\vec{w}</tex> равно нулю. Нулевые веса для некоторых признаков равносильны их исключению из модели (признание их неинформативными). | ||
| + | |||
| + | ==== Двойственная задача ==== | ||
| + | |||
| + | Рассмотрим получение двойственной задачи оптимизации для задачи (1). Для этого рассмотрим эквивалентную постановку данной задачи в виде задачи условной оптимизации: | ||
| + | |||
| + | <tex>\begin{cases}&\frac{1}{2}\vec{z}^T\vec{z} + \lambda ||\vec{w}||_1\rightarrow\min_{\vec{z},\vec{w}},\\ &X\vec{w}-\vec{t} = \vec{z}.\end{cases}</tex> | ||
| + | |||
| + | Далее можно показать, что двойственной к данной задаче выпуклой оптимизации будет следующая: | ||
| + | |||
| + | <tex>\begin{cases}&-\frac{1}{2}\vec{\mu}^T\vec{\mu} - \vec{\mu}^T\vec{t}\rightarrow\max_{\vec{\mu}},\\ &||X^T\vec{\mu}||_{\infty}\le\lambda.\end{cases}\qquad (2)</tex> | ||
| + | |||
| + | Здесь под <tex>||\vec{y}||_{\infty}</tex> понимается <tex>\max(|y_1|,\dots,|y_D|)</tex>. | ||
| + | |||
| + | ==== Гладкая задача ==== | ||
| + | |||
| + | Задачу выпуклой негладкой оптимизации (1) можно эквивалентно представить в виде задачи гладкой условной минимизации: | ||
| + | |||
| + | <tex>\begin{cases}&\frac{1}{2}||\vec{t}-X\vec{w}||^2 + \lambda\sum_{d=1}^Du_d\rightarrow\min_{\vec{w},\vec{u}},\\ &-u_d\le w_d\le u_d,\ \forall d = 1,\dots,D.\end{cases}\qquad (3)</tex> | ||
=== Формулировка задания === | === Формулировка задания === | ||
| - | * Вывести двойственную задачу оптимизации | + | * Вывести двойственную задачу оптимизации (2); записать, как по решению двойственной задачи (2) можно получить решение прямой задачи (1); |
| - | * Для | + | * Для задачи (2) предложить формулу вычисления допустимой двойственной точки <tex>\vec{\mu}</tex> по заданной прямой точке <tex>\vec{w}</tex>, на ее основе записать верхнюю оценку на зазор между решениями прямой задачи (1) и двойственной задачи (2); |
| - | * Вывести необходимые формулы для решения гладкой задачи обучения ( | + | * Вывести необходимые формулы для решения гладкой задачи обучения (3) с помощью метода барьерных функций; предложить свой способ эффективного решения соответствующей СЛАУ, необходимые для этого формулы вставить в отчет; |
| - | * Реализовать метод барьерных | + | * Реализовать метод барьерных функций для решения задачи (3); в качестве критерия останова использовать полученную верхнюю оценку на зазор; |
| - | * Вывести необходимые формулы для решения | + | * Вывести необходимые формулы для решения задачи (2) с помощью прямо-двойственного метода внутренней точки; предложить свой способ эффективного решения возмущенной ККТ-системы, необходимые для этого формулы вставить в отчет; |
| - | * Реализовать прямо-двойственный метод внутренней точки для | + | * Реализовать прямо-двойственный метод внутренней точки для задачи (2); в качестве критерия останова использовать норму правой части возмущенной ККТ-системы; |
| - | * Реализовать на выбор проксимальный или покоординатный метод для решения задачи обучения | + | * Реализовать на выбор проксимальный или покоординатный метод для решения задачи обучения (1); |
| - | * Провести экспериментальное сравнение трех реализованных методов на предмет скорости работы при 1) различных | + | * Провести экспериментальное сравнение трех реализованных методов (метод барьеров для задачи (1), прямо-двойственный метод внутренней точки для задачи (2) и проксимальный/покоординатный метод для задачи (1)) на предмет скорости работы при 1) различных соотношениях между количеством объектов и признаков в данных и 2) различных значениях параметра точности <tex>\varepsilon</tex>; |
| - | * Написать отчет в формате PDF с описанием всех проведенных исследований. Данный отчет должен содержать, в частности, | + | * Написать отчет в формате PDF с описанием всех проведенных исследований. Данный отчет должен содержать, в частности, необходимые формулы для всех методов. Также во всех приведенных экспериментах должно быть указано количество итераций, точность, параметры и время работы методов. |
=== Спецификация реализуемых функций === | === Спецификация реализуемых функций === | ||
{|class="standard" | {|class="standard" | ||
| - | !'' | + | !''Обучение методом штрафных функций'' |
|- | |- | ||
| - | | | + | |w = '''l1linreg_barrier'''(X, t, lambda, param_name1, param_value1, ...) |
|- | |- | ||
|ВХОД | |ВХОД | ||
| Строка 37: | Строка 67: | ||
| | | | ||
{|border="0" | {|border="0" | ||
| - | | | + | |X — обучающая выборка, матрица размера NxD; |
|- | |- | ||
| - | | | + | |t — регрессионные значения, вектор длины N; |
| + | |- | ||
| + | |lambda — параметр регуляризации, число; | ||
|- | |- | ||
|(param_name, param_value) — необязательные параметры, следующие названия и значения возможны: | |(param_name, param_value) — необязательные параметры, следующие названия и значения возможны: | ||
| Строка 45: | Строка 77: | ||
| | | | ||
{|border="0" | {|border="0" | ||
| - | |'eps' — точность оптимизации по | + | |'eps' — точность оптимизации по зазору, число, по умолчанию = 1e-5; |
|- | |- | ||
| - | |'max_iter' — максимальное число итераций, число, по умолчанию = | + | |'max_iter' — максимальное число внешних итераций, число, по умолчанию = 100; |
|- | |- | ||
| - | |' | + | |'max_iter2' — максимальное число внутренних итераций, число, по умолчанию = 10; |
|- | |- | ||
| - | + | |'t_params' — стратегия увеличения параметра центрирования <tex>\tau</tex>, вектор из двух чисел <tex>[\tau_{start},\ v]</tex>, по умолчанию = [1 10]; | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | |' | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
|- | |- | ||
| - | |' | + | |'b_params' — параметры для стратегии backtracking при поиске длины шага, вектор из трех чисел [alpha, beta, rho], по умолчанию = [1 0.5 0.1]; |
|- | |- | ||
| - | |'display' — режим отображения, true или false, по умолчанию = false; | + | |'display' — режим отображения, true или false, если true, то отображаются текущие показатели метода на каждой итерации, по умолчанию = false; |
|- | |- | ||
|} | |} | ||
| Строка 111: | Строка 97: | ||
| | | | ||
{| | {| | ||
| - | | | + | |w — найденные веса, вектор длины D. |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
|} | |} | ||
|} | |} | ||
| + | |||
| + | Аналогично выглядят прототипы функций ''l1linreg_pd'' для прямо-двойственного метода решения двойственной задачи, ''l1linreg_prox'' для проксимального метода и ''l1linreg_cd'' для метода покоординатного спуска. | ||
=== Оформление задания === | === Оформление задания === | ||
| Строка 134: | Строка 109: | ||
Письмо должно содержать: | Письмо должно содержать: | ||
*PDF-файл с описанием проведенных исследований; | *PDF-файл с описанием проведенных исследований; | ||
| - | *Файлы | + | *Файлы l1linreg_barrier, l1linreg_pd, l1linreg_prox или l1linreg_cd; |
*Набор вспомогательных файлов при необходимости. | *Набор вспомогательных файлов при необходимости. | ||
[[Категория:Учебные курсы]] | [[Категория:Учебные курсы]] | ||
Текущая версия
Начало выполнения задания: 23 ноября 2012
Срок сдачи: 6 декабря 2012 (четверг), 23:59
Среда реализации задания – MATLAB.
Модель 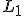 -регуляризованной линейной регрессии
-регуляризованной линейной регрессии
Формулировка метода
Рассматривается задача восстановления регрессии. Имеется обучающая выборка , где
— вектор признаков для объекта
, а
— его регрессионное значение. Задача заключается в прогнозировании регрессионного значения
для нового объекта, представленного своим вектором признаков
.
В линейной регрессии прогнозирование осуществляется с помощью линейной функции:
,
где — некоторые веса. Настройка весов осуществляется путем минимизации следующего регуляризованного критерия:
Здесь — задаваемый пользователем параметр регуляризации. Использование
-регуляризации позволяет, во-первых, снизить вероятность переобучения алгоритма, а во-вторых, получить т.н. разреженное решение. В разреженном решении часть компонент оптимального вектора весов
равно нулю. Нулевые веса для некоторых признаков равносильны их исключению из модели (признание их неинформативными).
Двойственная задача
Рассмотрим получение двойственной задачи оптимизации для задачи (1). Для этого рассмотрим эквивалентную постановку данной задачи в виде задачи условной оптимизации:
Далее можно показать, что двойственной к данной задаче выпуклой оптимизации будет следующая:
Здесь под понимается
.
Гладкая задача
Задачу выпуклой негладкой оптимизации (1) можно эквивалентно представить в виде задачи гладкой условной минимизации:
Формулировка задания
- Вывести двойственную задачу оптимизации (2); записать, как по решению двойственной задачи (2) можно получить решение прямой задачи (1);
- Для задачи (2) предложить формулу вычисления допустимой двойственной точки
по заданной прямой точке
, на ее основе записать верхнюю оценку на зазор между решениями прямой задачи (1) и двойственной задачи (2);
- Вывести необходимые формулы для решения гладкой задачи обучения (3) с помощью метода барьерных функций; предложить свой способ эффективного решения соответствующей СЛАУ, необходимые для этого формулы вставить в отчет;
- Реализовать метод барьерных функций для решения задачи (3); в качестве критерия останова использовать полученную верхнюю оценку на зазор;
- Вывести необходимые формулы для решения задачи (2) с помощью прямо-двойственного метода внутренней точки; предложить свой способ эффективного решения возмущенной ККТ-системы, необходимые для этого формулы вставить в отчет;
- Реализовать прямо-двойственный метод внутренней точки для задачи (2); в качестве критерия останова использовать норму правой части возмущенной ККТ-системы;
- Реализовать на выбор проксимальный или покоординатный метод для решения задачи обучения (1);
- Провести экспериментальное сравнение трех реализованных методов (метод барьеров для задачи (1), прямо-двойственный метод внутренней точки для задачи (2) и проксимальный/покоординатный метод для задачи (1)) на предмет скорости работы при 1) различных соотношениях между количеством объектов и признаков в данных и 2) различных значениях параметра точности
;
- Написать отчет в формате PDF с описанием всех проведенных исследований. Данный отчет должен содержать, в частности, необходимые формулы для всех методов. Также во всех приведенных экспериментах должно быть указано количество итераций, точность, параметры и время работы методов.
Спецификация реализуемых функций
| Обучение методом штрафных функций | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| w = l1linreg_barrier(X, t, lambda, param_name1, param_value1, ...) | |||||||||||
| ВХОД | |||||||||||
| |||||||||||
| ВЫХОД | |||||||||||
|
Аналогично выглядят прототипы функций l1linreg_pd для прямо-двойственного метода решения двойственной задачи, l1linreg_prox для проксимального метода и l1linreg_cd для метода покоординатного спуска.
Оформление задания
Выполненный вариант задания необходимо прислать письмом по адресу bayesml@gmail.com с темой «[МОМО12] Задание 3. ФИО». Убедительная просьба присылать выполненное задание только один раз с окончательным вариантом. Новые версии будут рассматриваться только в самом крайнем случае. Также убедительная просьба строго придерживаться заданной выше спецификации реализуемых функций.
Письмо должно содержать:
- PDF-файл с описанием проведенных исследований;
- Файлы l1linreg_barrier, l1linreg_pd, l1linreg_prox или l1linreg_cd;
- Набор вспомогательных файлов при необходимости.