Метод Ньютона. Проблема области сходимости. Метод парабол. Совмещение методов Ньютона и парабол
Материал из MachineLearning.
Содержание |
Постановка задачи одномерной оптимизации
Задача одномерной оптимизации определяется следующим образом:
- Допустимое множество — множество
;
- Целевую функцию — отображение
;
- Критерий поиска (max или min).
Тогда решить задачу означает одно из:
- Показать, что
.
- Показать, что целевая функция
не ограничена.
- Найти
.
- Если
, то найти
.
Если минимизируемая функция не является выпуклой, то часто ограничиваются поиском локальных минимумов и максимумов: точек таких, что всюду в некоторой их окрестности
для минимума и
для максимума.
Если допустимое множество , то такая задача называется задачей безусловной оптимизации, в противном случае — задачей условной оптимизации.
Метод Ньютона
Это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643—1727), под именем которого и обрёл свою известность. Поиск решения осуществляется путём построения последовательных приближений и основан на принципах простой итерации. Метод обладает квадратичной сходимостью. В случае решения задач оптимизации предполагается, что функция дважды непрерывно дифференцируема. Отыскание минимума функции
производится при помощи отыскания стационарной точки, т.е. точки
, удовлетворяющей уравнению
, которое решается методом Ньютона.
Если – точка, полученная на k-м шаге, то функция
аппроксимируется своим уравнением касательной:
а точка выбирается как пересечение этой прямой с осью
, т.е.
.
Неудобство этого метода состоит в необходимости вычисления в каждой точке первой и второй производных. Значит, он применим лишь тогда, когда функция имеет достаточно простую аналитическую форму, чтобы производные могли быть вычислены в явном виде вручную. Действительно, всякий раз, когда решается новая задача, необходимо выбрать две специфические подпрограммы (функции) вычисления производных
и
, что не позволяет построить общие алгоритмы, т.е. применимые к функции любого типа.
Когда начальная точка итераций достаточно близка к искомому минимуму, скорость сходимости метода Ньютона в общем случае квадратическая. Однако, глобальная сходимость метода Ньютона, вообще говоря, не гарантируется.
Хороший способ гарантировать глобальную сходимость этого метода состоит в комбинировании его с другим методом для быстрого получения хорошей аппроксимации искомого оптимума. Тогда несколько итераций метода Ньютона, с этой точкой в качестве исходной, достаточны для получения превосходной точности.
Ограничения
Пускай задано уравнение , где
и надо найти его решение.
Ниже приведена формулировка основной теоремы, которая позволяет дать чёткие условия применимости. Теорема Канторовича.
Если существуют такие константы , что:
-
на
, то есть
существует и не равна нулю;
-
на
, то есть
ограничена;
-
на
, и
;
Причём длина рассматриваемого отрезка . Тогда справедливы следующие утверждения:
- на
существует корень
уравнения
;
- если
, то итерационная последовательность сходится к этому корню:
;
- погрешность может быть оценена по формуле
.
Из последнего из утверждений теоремы в частности следует квадратичная сходимость метода:
Тогда ограничения на исходную функцию будут выглядеть так:
- функция должна быть ограничена;
- функция должна быть гладкой, дважды дифференцируемой;
- её первая производная
равномерно отделена от нуля;
- её вторая производная
должна быть равномерно ограничена.
В случае решения задачи оптимизации под функцией понимаем ее производную.
Проблема области сходимости
Запишем итерационный процесс:
.
Известно, что условием сходимости этого процесса будет неравенство
,
где , отсюда получем условие сходимости:
.
В силу того что мы ищем корень уравнения , существует такая окрестность, где
, но в общем случае эта область будет мала, то есть нужно подбирать начальное приближение достаточно близко расположенным к корню.
Теорма о сходимости метода Ньютона
Пусть - простой вещественный корень уравнения
, а функция
- дважды дифференцируема в некоторой окрестности
, причем первая произодная нигде не обращается в нуль.
Тогда, следуя обозначениям
,
При выборе начального приближения из той же окрестности
такого, что
,
итерационная последовательность
будет сходиться к , причем для погрешности на k-м шаге буддет справедлива оценка:
.
Метод парабол
Относительно метода Ньютона этот метод обладает тем преимуществом, что он не требует вычисления производных функции . Однако, его сходимость может быть гарантирована лишь для достаточно регулярных функций (непрерывных и много раз дифференцируемых).
В этом методе вычисляется значение функции сразу в трех близлежащих точках ,
,
, где h – малое число. Через эти три точки проводится интерполяционная парабола:
.
Минимум параболы достигается при , т.е. при
. Для трех точек получаем систему трех линейных уравнений для коэффициентов a, b, c. Находим a и b и тогда:
.
Числовой пример
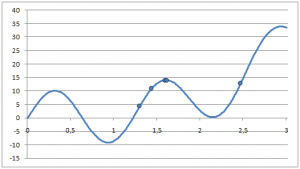
Сравним работу методов Ньютона и парабол на примере много экстремальной функции при одинаковом начальном приближении:
| | | | | |
|---|---|---|---|---|
| 0 | 1.3 | 1.3 | 53.89938129 | 53.89938129 |
| 1 | 2.472235424 | 2.472080749 | 67.28692280 | 67.27673489 |
| 2 | 1.449211232 | 1.452275085 | 34.85893188 | 34.25354559 |
| 3 | 1.626598277 | 1.624678936 | -5.832725638 | -5.389540219 |
| 4 | 1.601301575 | 1.601390533 | 0.095723918 | 0.074598093 |
| 5 | 1.60170464 | 1.601718525 | 1.59821E-05 | -0.003280363 |
| 6 | 1.601704707 | 1.601718641 | 4.0945E-13 | -0.00330785 |
Код функций на С++, с помощью которых были произведены все расчеты можно скачать тут.
Литература
- А.А.Самарский, А.В.Гулин. Численные методы М.: Наука, 1989.
- А.А.Самарский. Введение в численные методы М.: Наука, 1982.
- Н.В.Соснин. Численные методы. Конспект лекций (сост. Д.В.Ховратович, Е.А.Попов).
- М.М.Потапов. Методы оптимизаций. Конспект лекций (сост. М.Л.Буряков).
- Е.А.Волков. Численные методы. — М.: Физматлит, 2003.