Регрессионный анализ
Материал из MachineLearning.
м (→О терминах: викификация) |
м (→О терминах: исправление очипятки) |
||
| (22 промежуточные версии не показаны) | |||
| Строка 8: | Строка 8: | ||
Регрессионный анализ — раздел [[математическая статистика|математической статистики]] и [[машинное обучение|машинного обучения]]. | Регрессионный анализ — раздел [[математическая статистика|математической статистики]] и [[машинное обучение|машинного обучения]]. | ||
Предполагается, что зависимая переменная есть сумма значений некоторой модели и [[случайная величина|случайной величины]]. | Предполагается, что зависимая переменная есть сумма значений некоторой модели и [[случайная величина|случайной величины]]. | ||
| - | Относительно характера распределения этой величины делаются | + | Относительно характера распределения этой величины делаются предположения, называемые гипотезой порождения данных. |
Для подтверждения или опровержения этой гипотезы выполняются [[статистический тест|статистические тесты]], | Для подтверждения или опровержения этой гипотезы выполняются [[статистический тест|статистические тесты]], | ||
называемые [[анализ остатков|анализом остатков]]. | называемые [[анализ остатков|анализом остатков]]. | ||
| Строка 15: | Строка 15: | ||
[[тестирование гипотез|тестирования гипотез]] и выявления скрытых взаимосвязей в данных. | [[тестирование гипотез|тестирования гипотез]] и выявления скрытых взаимосвязей в данных. | ||
| - | == Определение == | + | == Определение регрессионного анализа == |
[[Изображение:Regression_Analysis_Regression.gif|frame|right|Выборка может быть не функцией, а отношением. Например, данные для | [[Изображение:Regression_Analysis_Regression.gif|frame|right|Выборка может быть не функцией, а отношением. Например, данные для | ||
построения регрессии могут быть такими: <tex>\{(0,0),(0,1),(0,2),(1,1),(1,2),(1,3)\}</tex>. В такой выборке одному значению | построения регрессии могут быть такими: <tex>\{(0,0),(0,1),(0,2),(1,1),(1,2),(1,3)\}</tex>. В такой выборке одному значению | ||
| Строка 40: | Строка 40: | ||
== Линейная регрессия == | == Линейная регрессия == | ||
| + | {{main|Многомерная линейная регрессия}} | ||
| + | |||
Линейная регрессия предполагает, что функция <tex>f</tex> зависит от параметров <tex>\mathbf{w}</tex> линейно. | Линейная регрессия предполагает, что функция <tex>f</tex> зависит от параметров <tex>\mathbf{w}</tex> линейно. | ||
При этом линейная зависимость от свободной переменной <tex>\mathbf{x}</tex> необязательна, | При этом линейная зависимость от свободной переменной <tex>\mathbf{x}</tex> необязательна, | ||
| - | <center><tex> y=f(\mathbf{w},\mathbf{x})+\nu=\sum_{j=1}^ | + | <center><tex> y=f(\mathbf{w},\mathbf{x})+\nu=\sum_{j=1}^N w_jg_j(\mathbf{x})+\nu. </tex></center> |
В случае, когда функция <tex>g\equiv\text{id}</tex> линейная регрессия имеет вид | В случае, когда функция <tex>g\equiv\text{id}</tex> линейная регрессия имеет вид | ||
<center><tex> y=\sum_{j=1}^N w_jx_j+\nu=\langle\mathbf{w},\mathbf{x}\rangle +\nu, </tex></center> | <center><tex> y=\sum_{j=1}^N w_jx_j+\nu=\langle\mathbf{w},\mathbf{x}\rangle +\nu, </tex></center> | ||
| Строка 49: | Строка 51: | ||
Значения параметров в случае линейной регрессии находят с помощью [[метод наименьших квадратов|метода наименьших квадратов]]. | Значения параметров в случае линейной регрессии находят с помощью [[метод наименьших квадратов|метода наименьших квадратов]]. | ||
Использование этого метода обосновано предположением о [[гауссовское распределение|гауссовском распределении]] случайной переменной. | Использование этого метода обосновано предположением о [[гауссовское распределение|гауссовском распределении]] случайной переменной. | ||
| - | + | ||
| + | Разности <tex>y_i-f(\mathbf{x}_i)</tex> между фактическими значениями зависимой переменной и восстановленными называются '''регрессионными остатками''' (residuals). В литературе используются также синонимы: ''невязки'' и ''ошибки''. | ||
| + | Одной из важных оценок критерия качества полученной зависимости является сумма квадратов остатков: | ||
<center><tex>SSE=\|f(\mathbf{x}_i)-y_i\|_2=\sum_{i=1}^N(y_i-f(\mathbf{w},\mathbf{x}_i))^2.</tex></center> | <center><tex>SSE=\|f(\mathbf{x}_i)-y_i\|_2=\sum_{i=1}^N(y_i-f(\mathbf{w},\mathbf{x}_i))^2.</tex></center> | ||
| - | Здесь <tex>SSE</tex> — Sum of Squared Errors | + | Здесь <tex>SSE</tex> — Sum of Squared Errors. |
| - | + | ||
Дисперсия остатков вычисляется по формуле | Дисперсия остатков вычисляется по формуле | ||
<center><tex>\bar{\sigma}^2_\nu=\frac{SSE}{N-2}=MSE.</tex></center> | <center><tex>\bar{\sigma}^2_\nu=\frac{SSE}{N-2}=MSE.</tex></center> | ||
| Строка 68: | Строка 72: | ||
== Нелинейная регрессия == | == Нелинейная регрессия == | ||
| + | {{main|Нелинейная регрессия}} | ||
| + | |||
Нелинейные регрессионные модели — [[регрессионная модель|модели]] вида | Нелинейные регрессионные модели — [[регрессионная модель|модели]] вида | ||
::<tex>y=f(\mathbf{w},\mathbf{x})+\nu,</tex> | ::<tex>y=f(\mathbf{w},\mathbf{x})+\nu,</tex> | ||
| Строка 76: | Строка 82: | ||
<tex>\nu</tex> — случайная величина и <tex>\mathbf{g}=[g_1,\ldots, g_n]</tex> — функция из некоторого | <tex>\nu</tex> — случайная величина и <tex>\mathbf{g}=[g_1,\ldots, g_n]</tex> — функция из некоторого | ||
заданного множества. | заданного множества. | ||
| + | |||
| + | Значения параметров в случае нелинейной регрессии находят с помощью одного из методов градиентного спуска, например [[алгоритм Левенберга-Марквардта|алгоритма Левенберга-Марквардта]]. | ||
== О терминах == | == О терминах == | ||
| - | Термин "регрессия" был | + | Термин "регрессия" был введён Фрэнсисом Гальтоном в конце 19-го века. |
Гальтон обнаружил, что дети родителей с высоким или низким ростом обычно не наследуют выдающийся рост и назвал этот | Гальтон обнаружил, что дети родителей с высоким или низким ростом обычно не наследуют выдающийся рост и назвал этот | ||
феномен "регрессия к посредственности". | феномен "регрессия к посредственности". | ||
| Строка 103: | Строка 111: | ||
Различают <i>параметрическую</i> и <i>непараметрическую</i> регрессию. | Различают <i>параметрическую</i> и <i>непараметрическую</i> регрессию. | ||
Строгую границу между этими двумя типами регрессий провести сложно. | Строгую границу между этими двумя типами регрессий провести сложно. | ||
| - | Сейчас | + | Сейчас не существует общепринятого критерия отличия одного типа моделей от другого. |
Например, считается, что линейные модели являются параметрическими, а модели, включающие усреднение зависимой переменной по пространству свободной переменной —непараметрическими. | Например, считается, что линейные модели являются параметрическими, а модели, включающие усреднение зависимой переменной по пространству свободной переменной —непараметрическими. | ||
Пример параметрической регресионной модели: линейный предиктор, многослойный персептрон. | Пример параметрической регресионной модели: линейный предиктор, многослойный персептрон. | ||
| Строка 138: | Строка 146: | ||
Регрессия и классификация тесно связаны друг с другом. | Регрессия и классификация тесно связаны друг с другом. | ||
| - | Термин <i>[[алгоритм]]</i> в классификации мог бы стать синонимом термина <i>[[модель]]</i> в регрессии, | + | Термин <i>[[алгоритм]]</i> в классификации мог бы стать синонимом термина <i>[[регрессионная модель|модель]]</i> в регрессии, |
если бы алгоритм не оперировал с дискретным множеством ответов-классов, а модель — с непрерывно-определенной свободной переменной. | если бы алгоритм не оперировал с дискретным множеством ответов-классов, а модель — с непрерывно-определенной свободной переменной. | ||
== Смотри также == | == Смотри также == | ||
* [[Регрессионная модель]] | * [[Регрессионная модель]] | ||
| + | * [[Линейная регрессия (пример)]] | ||
* [[Метод наименьших квадратов]] | * [[Метод наименьших квадратов]] | ||
| - | * [[ | + | * [[Нелинейная регрессия]] |
| + | * [[Алгоритм Левенберга-Марквардта]] | ||
| + | * [[Связанный Байесовский вывод]] | ||
* [[Метод группового учета аргументов]] | * [[Метод группового учета аргументов]] | ||
* [[Анализ регрессионных остатков]] | * [[Анализ регрессионных остатков]] | ||
| - | + | * [[:Категория:Практика и вычислительные эксперименты|Применение методов регрессионного анализа на практике]] | |
| + | * [[Регрессионный анализ (рекомендуемые обозначения)]] | ||
== Литература == | == Литература == | ||
* Дрейпер Н., Смит Г. Прикладной регрессионный анализ. М.: Издательский дом «Вильямс». 2007. | * Дрейпер Н., Смит Г. Прикладной регрессионный анализ. М.: Издательский дом «Вильямс». 2007. | ||
* Айвазян С.А. Прикладная статистика и основы эконометрики. М.: Юнити. 2001. | * Айвазян С.А. Прикладная статистика и основы эконометрики. М.: Юнити. 2001. | ||
* Брандт З. Анализ данных. М.: Мир. 2003. | * Брандт З. Анализ данных. М.: Мир. 2003. | ||
| + | * Стрижов В. В. Методы индуктивного порождения регрессионных моделей. М.: ВЦ РАН. 2008. 55 с. [[Media:strijov08ln.pdf|Брошюра, PDF]]. | ||
| + | * Стрижов В.В., Крымова Е.А. Методы выбора регрессионных моделей. М.: ВЦ РАН, 2010. 60 с. [[Media:Strijov-Krymova10Model-Selection.pdf|Брошюра, PDF]]. | ||
== Внешние ссылки == | == Внешние ссылки == | ||
| Строка 161: | Строка 175: | ||
[[Категория:Регрессионный анализ]] | [[Категория:Регрессионный анализ]] | ||
[[Категория:Энциклопедия анализа данных]] | [[Категория:Энциклопедия анализа данных]] | ||
| + | [[Категория:Популярные и обзорные статьи]] | ||
Текущая версия
Регрессионный анализ — метод моделирования измеряемых данных и исследования их свойств. Данные состоят из пар значений зависимой переменной (переменной отклика) и независимой переменной (объясняющей переменной). Регрессионная модель есть функция независимой переменной и параметров с добавленной случайной переменной. Параметры модели настраиваются таким образом, что модель наилучшим образом приближает данные. Критерием качества приближения (целевой функцией) обычно является среднеквадратичная ошибка: сумма квадратов разности значений модели и зависимой переменной для всех значений независимой переменной в качестве аргумента. Регрессионный анализ — раздел математической статистики и машинного обучения. Предполагается, что зависимая переменная есть сумма значений некоторой модели и случайной величины. Относительно характера распределения этой величины делаются предположения, называемые гипотезой порождения данных. Для подтверждения или опровержения этой гипотезы выполняются статистические тесты, называемые анализом остатков. При этом предполагается, что независимая переменная не содержит ошибок. Регрессионный анализ используется для прогноза, анализа временных рядов, тестирования гипотез и выявления скрытых взаимосвязей в данных.
Содержание |
Определение регрессионного анализа
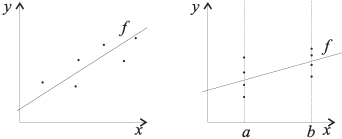
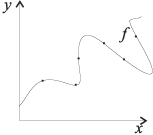
Регрессия — зависимость математического ожидания (например, среднего значения)
случайной величины от одной или нескольких других случайных величин (свободных переменных),
то есть .
Регрессионным анализом называется поиск такой функции
, которая описывает эту зависимость.
Регрессия может быть представлена в виде суммы неслучайной и случайной составляющих.
где — функция регрессионной зависимости, а
— аддитивная случайная величина с нулевым матожиданием.
Предположение о характере распределения этой величины называется гипотезой порождения данных.
Обычно предполагается, что величина
имеет гауссово распределение с нулевым средним и дисперсией
.
Задача нахождения регрессионной модели нескольких свободных переменных ставится следующим образом.
Задана выборка — множество значений свободных
переменных и множество
соответствующих им значений зависимой переменной.
Эти множества обозначаются как
, множество исходных данных
.
Задана регрессионная модель — параметрическое семейство функций
зависящая от параметров
и свободных переменных
.
Требуется найти наиболее вероятные параметры
:
Функция вероятности зависит от гипотезы порождения данных и задается Байесовским выводом или методом наибольшего правдоподобия.
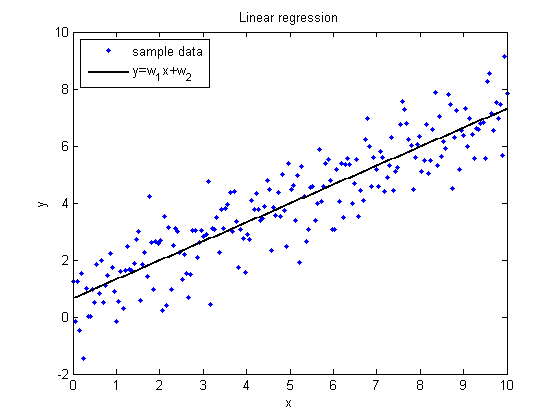
Линейная регрессия
Линейная регрессия предполагает, что функция зависит от параметров
линейно.
При этом линейная зависимость от свободной переменной
необязательна,
В случае, когда функция линейная регрессия имеет вид
здесь — компоненты вектора
.
Значения параметров в случае линейной регрессии находят с помощью метода наименьших квадратов. Использование этого метода обосновано предположением о гауссовском распределении случайной переменной.
Разности между фактическими значениями зависимой переменной и восстановленными называются регрессионными остатками (residuals). В литературе используются также синонимы: невязки и ошибки.
Одной из важных оценок критерия качества полученной зависимости является сумма квадратов остатков:
Здесь — Sum of Squared Errors.
Дисперсия остатков вычисляется по формуле
Здесь — Mean Square Error, среднеквадратичная ошибка.
На графиках представлены выборки, обозначенные синими точками, и регрессионные зависимости, обозначенные сплошными линиями. По оси абсцисс отложена свободная переменная, а по оси ординат — зависимая. Все три зависимости линейны относительно параметров.
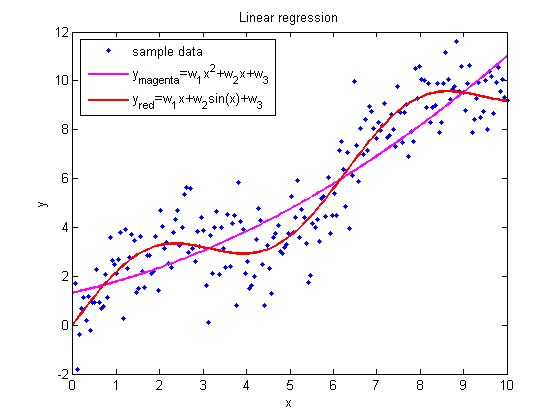
Нелинейная регрессия
Нелинейные регрессионные модели — модели вида
которые не могут быть представлены в виде скалярного произведения
где — параметры регрессионной модели,
— свободная переменная из пространства
,
— зависимая переменная,
— случайная величина и
— функция из некоторого
заданного множества.
Значения параметров в случае нелинейной регрессии находят с помощью одного из методов градиентного спуска, например алгоритма Левенберга-Марквардта.
О терминах
Термин "регрессия" был введён Фрэнсисом Гальтоном в конце 19-го века. Гальтон обнаружил, что дети родителей с высоким или низким ростом обычно не наследуют выдающийся рост и назвал этот феномен "регрессия к посредственности". Сначала этот термин использовался исключительно в биологическом смысле. После работ Карла Пирсона этот термин стали использовать и в статистике.
В статистической литературе различают регрессию с участием одной свободной переменной и с несколькими свободными переменными —
одномерную и многомерную регрессию.
Предполагается, что мы используем несколько свободных переменных,
то есть, свободная переменная — вектор .
В частных случаях, когда свободная переменная является скаляром,
она будет обозначаться
.
Различают линейную и нелинейную регрессию.
Если регрессионную модель не является линейной комбинацией функций
от параметров, то говорят о нелинейной регрессии.
При этом модель может быть произвольной суперпозицией функций
из некоторого набора.
Нелинейными моделями являются, экспоненциальные,
тригонометрические и другие (например, радиальные базисные функции или персептрон Розенблатта),
полагающие зависимость между параметрами и зависимой переменной нелинейной.
Различают параметрическую и непараметрическую регрессию. Строгую границу между этими двумя типами регрессий провести сложно. Сейчас не существует общепринятого критерия отличия одного типа моделей от другого. Например, считается, что линейные модели являются параметрическими, а модели, включающие усреднение зависимой переменной по пространству свободной переменной —непараметрическими. Пример параметрической регресионной модели: линейный предиктор, многослойный персептрон. Примеры смешанной регрессионной модели: функции радиального базиса. Непараметрическая модель — скользящее усреднение в окне некоторой ширины. В целом, непараметрическая регрессия отличается от параметрической тем, что зависимая переменная зависит не от одного значения свободной переменной, а от некоторой заданной окрестности этого значения.
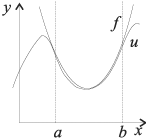
Есть различие между терминами: "приближение функций", "аппроксимация", "интерполяция", и "регрессия". Оно заключается в следующем.
Приближение функций. Дана функция дискретного или непрерывного аргумента.
Требуется найти функцию
из некоторого параметрическую семейства, например, среди алгебраических
полиномов заданной степени. Параметры функции
должны
доставлять минимум некоторому функционалу, например,
Термин аппроксимация — синоним термина "приближение функций".
Чаще используется тогда, когда речь идет о заданной функции, как о функции дискретного аргумента.
Здесь также требуется отыскать такую функцию , которая проходит наиболее близко ко всем точкам заданной функции.
При этом вводится понятие невязки — расстояния между точками непрерывной функции
и соответствующими точками функции
дискретного аргумента.
Интерполяция функций — частный случай задачи приближения,
когда требуется, чтобы в определенных точках, называемых
узлами интерполяции совпадали значения функции и
приближающей ее функции
. В более общем случае накладываются
ограничения на значения некоторых производных
производных.
То есть, дана функция
дискретного аргумента.
Требуется отыскать такую функцию
, которая проходит через все точки
.
При этом метрика обычно не используется, однако часто вводится понятие "гладкости" искомой функции.
Регрессия и классификация тесно связаны друг с другом. Термин алгоритм в классификации мог бы стать синонимом термина модель в регрессии, если бы алгоритм не оперировал с дискретным множеством ответов-классов, а модель — с непрерывно-определенной свободной переменной.
Смотри также
- Регрессионная модель
- Линейная регрессия (пример)
- Метод наименьших квадратов
- Нелинейная регрессия
- Алгоритм Левенберга-Марквардта
- Связанный Байесовский вывод
- Метод группового учета аргументов
- Анализ регрессионных остатков
- Применение методов регрессионного анализа на практике
- Регрессионный анализ (рекомендуемые обозначения)
Литература
- Дрейпер Н., Смит Г. Прикладной регрессионный анализ. М.: Издательский дом «Вильямс». 2007.
- Айвазян С.А. Прикладная статистика и основы эконометрики. М.: Юнити. 2001.
- Брандт З. Анализ данных. М.: Мир. 2003.
- Стрижов В. В. Методы индуктивного порождения регрессионных моделей. М.: ВЦ РАН. 2008. 55 с. Брошюра, PDF.
- Стрижов В.В., Крымова Е.А. Методы выбора регрессионных моделей. М.: ВЦ РАН, 2010. 60 с. Брошюра, PDF.