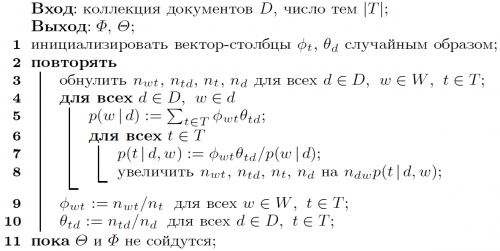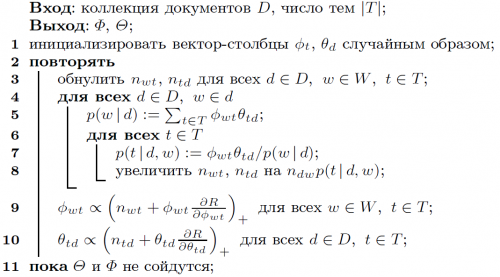Аддитивная регуляризация тематических моделей

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск
(→Литература)
(5 промежуточных версий не показаны.)
Строка 32: Строка 32:
Отсюда вытекают проблемы неустойчивости и плохой интерпретируемости тематических моделей.
Отсюда вытекают проблемы неустойчивости и плохой интерпретируемости тематических моделей.
 +
[[Изображение:PLSA-algorithm.png|500px|thumb|EM-алгоритм для PLSA]]
В [[PLSA|вероятностном латентном семантическом анализе]] (PLSA) для решения данной задачи используется [[EM-алгоритм]].
В [[PLSA|вероятностном латентном семантическом анализе]] (PLSA) для решения данной задачи используется [[EM-алгоритм]].
На каждой итерации ЕМ-алгоритма выполняется два шага:
На каждой итерации ЕМ-алгоритма выполняется два шага:
Строка 53: Строка 54:
при тех же ограничениях нормировки и неотрицательности.
при тех же ограничениях нормировки и неотрицательности.
 +
[[Изображение:ARTM-algorithm.png|500px|thumb|EM-алгоритм для ARTM]]
Для решения задачи регуляризованного правдоподобия используется EM-алгоритм с модифицированными формулами M-шага:
Для решения задачи регуляризованного правдоподобия используется EM-алгоритм с модифицированными формулами M-шага:
:::<tex>\phi_{wt} \propto \left(n_{wt} + \phi_{wt}\frac{\partial R}{\partial\phi_{wt}}\right)_{+},</tex>
:::<tex>\phi_{wt} \propto \left(n_{wt} + \phi_{wt}\frac{\partial R}{\partial\phi_{wt}}\right)_{+},</tex>
Строка 90: Строка 92:
* Не всякого рода знания удобно формализовать через априорные распределения. Попытка учесть больше знаний, чтобы построить более адекватную модель, приводит к значительному усложнению математического аппарата. В литературе почти нет работ по комбинированию тематических моделей, несмотря на их очевидную практическую востребованность.
* Не всякого рода знания удобно формализовать через априорные распределения. Попытка учесть больше знаний, чтобы построить более адекватную модель, приводит к значительному усложнению математического аппарата. В литературе почти нет работ по комбинированию тематических моделей, несмотря на их очевидную практическую востребованность.
* Не все верят, что естественный язык можно рассматривать как чисто статистическое явление. Одна из основных тенденций вычислительной лингвистики — создание гибридных моделей, объединяющих лучшие достижения статистических и лингвистических подходов. Лингвистические знания не всегда удобно описывать на вероятностном языке.
* Не все верят, что естественный язык можно рассматривать как чисто статистическое явление. Одна из основных тенденций вычислительной лингвистики — создание гибридных моделей, объединяющих лучшие достижения статистических и лингвистических подходов. Лингвистические знания не всегда удобно описывать на вероятностном языке.
-
* Многие байесовские модели используют априорные распределения Дирихле, имеющие весьма слабые лингвистические обоснования. Они не моделируют какие-либо явления естественного языка. Зато они удобны для математических выкладок благодаря свойству сопряжённости с мультиномиальным распределением.
+
* Большинство байесовских моделей вынужденно используют априорное распределение Дирихле. Оно математически удобно благодаря сопряжённости с мультиномиальным распределением. Однако оно не моделирует каких-либо явлений естественного языка и не имеет убедительных лингвистических обоснований. Более того, оно противоречит естественному требованию разреженности, не допуская чистых нулей в матрицах <tex>\Phi </tex> и <tex>\Theta</tex>.
* Априорное распределение Дирихле является слишком слабым регуляризатором. Проблему неустойчивости он не решает.
* Априорное распределение Дирихле является слишком слабым регуляризатором. Проблему неустойчивости он не решает.
Строка 104: Строка 106:
==Литература==
==Литература==
 +
# ''Воронцов К.В.'' [[Media:voron17survey-artm.pdf|Обзор вероятностных тематических моделей]]. 2018.
# ''Воронцов К. В.'' [[Media:Voron14dan-rus.pdf|Аддитивная регуляризация тематических моделей коллекций текстовых документов]] // Доклады РАН. 2014. — Т. 455., №3. 268–271
# ''Воронцов К. В.'' [[Media:Voron14dan-rus.pdf|Аддитивная регуляризация тематических моделей коллекций текстовых документов]] // Доклады РАН. 2014. — Т. 455., №3. 268–271
# ''Воронцов К. В. Потапенко А. А.'' [[Media:Voron14dialog.pdf|Регуляризация вероятностных тематических моделей для повышения интерпретируемости и определения числа тем]] // Компьютерная лингвистика и интеллектуальные технологии: По материалам ежегодной Международной конференции «Диалог» (Бекасово, 4–8 июня 2014 г.) Вып.13 (20). М: Изд-во РГГУ, 2014. C.676–687.
# ''Воронцов К. В. Потапенко А. А.'' [[Media:Voron14dialog.pdf|Регуляризация вероятностных тематических моделей для повышения интерпретируемости и определения числа тем]] // Компьютерная лингвистика и интеллектуальные технологии: По материалам ежегодной Международной конференции «Диалог» (Бекасово, 4–8 июня 2014 г.) Вып.13 (20). М: Изд-во РГГУ, 2014. C.676–687.
Строка 114: Строка 117:
* [[Тематическое моделирование]].
* [[Тематическое моделирование]].
* [[BigARTM]], [http://bigartm.org bigartm.org] — библиотека с открытым кодом для тематического моделирования больших коллекций.
* [[BigARTM]], [http://bigartm.org bigartm.org] — библиотека с открытым кодом для тематического моделирования больших коллекций.
-
* [[Вероятностные тематические модели (курс лекций, К.В.Воронцов)|Вероятностные тематические модели]] — семестровый спецкурс, [[Математические методы прогнозирования (кафедра ВМиК МГУ)|кафедра ММП]] [[ВМиК МГУ]].
 
* [[Коллекции документов для тематического моделирования]].
* [[Коллекции документов для тематического моделирования]].
 +
* [[Вероятностные тематические модели (курс лекций, К.В.Воронцов)|Вероятностные тематические модели]] — семестровый спецкурс, [[Математические методы прогнозирования (кафедра ВМиК МГУ)|кафедра ММП]] [[ВМиК МГУ]].
 +
* ''Воронцов К.В.'' Рекламная презентация про тематическое моделирование. [[Media:Voron-PTM-short.pdf|Voron-PTM-short.pdf]] {{важно|— обновление 14.03.2016}}.
 +
<!--
 +
* Тематическое моделирование в BigARTM: теория, алгоритмы, приложения. [[Media:Voron-2015-BigARTM.pdf|Voron-2015-BigARTM.pdf]].
* ''Воронцов К.В.'' Лекции по тематическому моделированию. [[Media:Voron-2013-ptm.pdf|Voron-2013-ptm.pdf]].
* ''Воронцов К.В.'' Лекции по тематическому моделированию. [[Media:Voron-2013-ptm.pdf|Voron-2013-ptm.pdf]].
-
* ''Воронцов К.В.'' Практическое задание по тематическому моделированию. [[Media:voron-2014-task-PTM.pdf|Voron-2014-task-ptm.pdf]].
+
-->
{{stub}}
{{stub}}
-
[[Категория:Инструменты и технологии]]
 
[[Категория:Тематическое моделирование]]
[[Категория:Тематическое моделирование]]
[[Категория:Анализ текстов]]
[[Категория:Анализ текстов]]
[[Категория:Машинное обучение]]
[[Категория:Машинное обучение]]

Версия 09:50, 5 мая 2018

Содержание

Аддитивная регуляризация тематических моделей — многокритериальный подход к построению вероятностных тематических моделей коллекций текстовых документов. Охватывает наиболее известные тематические модели PLSA, LDA и многие байесовские модели. Является альтернативой байесовскому обучению тематических моделей.

Основные отличия от байесовского подхода:

  • простой математический аппарат;
  • регуляризаторы не обязаны иметь вероятностную интерпретацию;
  • легко комбинировать регуляризаторы из разных моделей и строить многофункциональные тематические модели;
  • легко реализовать огромное разнообразие тематических моделей в одной библиотеке, см. BigARTM.

Теория

Тематическое моделирование

Основная статья: Тематическое моделирование

Вероятностное тематическое моделирование — это современный инструмент статистического анализа текстов, предназначенный для выявления тематики коллекций документов. Тематическая модель описывает каждую тему дискретным распределением на множестве терминов, каждый документ — дискретным распределением на множестве тем. Тематические модели используются для информационного поиска, классификации, категоризации, аннотирования, сегментации текстов.

Тематическая модель — это представление наблюдаемого условного распределения p(w|d) терминов (слов или словосочетаний) w в документах d коллекции D:

p(w|d) \;=\; \sum_{t\in T} p(w|t) p(t|d),

где T — множество тем;

\phi_{wt} = p(w|t) — неизвестное распределение терминов в теме t;
\theta_{td} = p(t|d) — неизвестное распределение тем в документе d.

Параметры тематической модели — матрицы \Phi=(\phi_{wt}) и \Theta=(\theta_{td}) находятся путём решения задачи максимизации правдоподобия

\sum_{d\in D} \sum_{w\in d} n_{dw}\log \sum_{t\in T} \phi_{wt}\theta_{td} \;\to\; \max_{\Phi,\Theta} ,

при ограничениях нормировки и неотрицательности

\sum_w \phi_{wt} = 1,\;\; \sum_t \theta_{td} = 1,\;\; \phi_{wt} \geq 0,\;\; \theta_{td}\geq 0,

где n_{dw} — число вхождений слова w в документ d.

Данная задача некорректно поставлена и имеет в общем случае бесконечно много решений вида (\Phi S) (S^{-1}\Theta) = \Phi\Theta. Отсюда вытекают проблемы неустойчивости и плохой интерпретируемости тематических моделей.

EM-алгоритм для PLSA
EM-алгоритм для PLSA

В вероятностном латентном семантическом анализе (PLSA) для решения данной задачи используется EM-алгоритм. На каждой итерации ЕМ-алгоритма выполняется два шага:

E-шаг:
p(t|d,w) \propto \phi_{wt} \theta_{td};
M-шаг:
\phi_{wt} \propto n_{wt},\;\;\; n_{wt} = \sum_{d\in D}n_{dw} p(t|d,w);
\theta_{td} \propto n_{td},\;\;\; n_{td} = \sum_{w\in d}n_{dw} p(t|d,w);

EM-алгоритм для PLSA сходится к одному из локальных решений.

Аддитивная регуляризация тематических моделей

Для решения проблемы неединственности и неустойчивости используется регуляризация. На искомое решение накладываются дополнительные ограничения.

Подход АРТМ основан на идее многокритериальной регуляризации. Он позволяет строить модели, удовлетворяющие многим ограничениям одновременно. Каждое ограничение формализуется в виде регуляризатора — оптимизационного критерия R_i(\Phi,\Theta)\to\max, зависящего от параметров модели. Взвешенная сума всех таких критериев

R(\Phi,\Theta) = \sum_{i=1}^k \tau_i R_i(\Phi,\Theta)

максимизируется совместно с основным критерием правдоподобия.

\sum_{d\in D} \sum_{w\in d} n_{dw}\log \sum_{t\in T} \phi_{wt}\theta_{td} \;+\; R(\Phi,\Theta)\;\to\; \max_{\Phi,\Theta} ,

при тех же ограничениях нормировки и неотрицательности.

EM-алгоритм для ARTM
EM-алгоритм для ARTM

Для решения задачи регуляризованного правдоподобия используется EM-алгоритм с модифицированными формулами M-шага:

\phi_{wt} \propto \left(n_{wt} + \phi_{wt}\frac{\partial R}{\partial\phi_{wt}}\right)_{+},
\theta_{td} \propto \left(n_{td} + \theta_{td}\frac{\partial R}{\partial\theta_{td}}\right)_{+}.

Для комбинирования регуляризаторов в АРТМ необходимо продумывать стратегию регуляризации:

  • какие регуляризаторы необходимы в данной задаче;
  • какие регуляризаторы должны работать одновременно, какие друг за другом или попеременно, делая необходимую подготовительную работу;
  • как менять коэффициент регуляризации каждого регуляризатора в ходе итераций: по каким условиям включать, усиливать, ослаблять и отключать каждый регуляризатор.

Ограничения подхода АРТМ:

  • Коэффициенты регуляризации приходится подбирать вручную. Автоматическая коррекция стратегий регуляризации в АРТМ пока является открытой проблемой.

Регуляризаторы

Следующие регуляризаторы реализованы в библиотеке BigARTM.

  • Сглаживание распределений терминов в темах. Используется для выделения фоновых тем, собирающих общую лексику языка или общую лексику данной коллекции.
  • Сглаживание распределений тем в документах. Используется для выделения фоновых слов в каждом документах.
  • Разреживание распределений терминов в темах. Используется для выделения лексических ядер предметных тем как относительно небольшой доли слов словаря.
  • Разреживание распределений тем в документах. Используется для выделения относительно небольшой доли предметных тем в каждом документах.
  • Декоррелирование распределений терминов в темах. Используется для повышения различности лексических ядер предметных тем.
  • Отбор тем путём обнуления вероятности темы во всех документах. Используется для выведения из модели незначимых тем. Позволяет оптимизировать число тем, начиная с заведомо избыточного числа тем и постепенно удаляя ненужные.

Модели PLSA и LDA

Две самые известные тематические модели — PLSA и LDA — реализуются как частные случаи в АРТМ:

  • PLSA (Probabilistic Latent Semantic Analysis) — это тематическая модель без регуляризаторов.
  • LDA (Latent Dirichlet Allocation) — это тематическая модель, в которой каждая тема сглажена одним и тем же регуляризатором Дирихле.

В АРТМ рекомендуется использовать небольшое число сглаженных тем (можно одну), чтобы моделировать общую лексику языка, а к остальным темам применять регуляризаторы разреживания и декоррелирования, чтобы помочь тематической модели выделить в них специфические темы предметных областей данной текстовой коллекции.

Сравнение с байесовскими моделями

Вероятностное тематическое моделирование развивается, главным образом, в рамках байесовского обучения и графических моделей. В байесовском подходе коллекция текстов описывается единой вероятностной порождающей моделью, при этом учёт дополнительных данных и формализация дополнительных ограничений производится через априорные распределения.

Это не очень хорошо по нескольким причинам:

  • Не всякого рода знания удобно формализовать через априорные распределения. Попытка учесть больше знаний, чтобы построить более адекватную модель, приводит к значительному усложнению математического аппарата. В литературе почти нет работ по комбинированию тематических моделей, несмотря на их очевидную практическую востребованность.
  • Не все верят, что естественный язык можно рассматривать как чисто статистическое явление. Одна из основных тенденций вычислительной лингвистики — создание гибридных моделей, объединяющих лучшие достижения статистических и лингвистических подходов. Лингвистические знания не всегда удобно описывать на вероятностном языке.
  • Большинство байесовских моделей вынужденно используют априорное распределение Дирихле. Оно математически удобно благодаря сопряжённости с мультиномиальным распределением. Однако оно не моделирует каких-либо явлений естественного языка и не имеет убедительных лингвистических обоснований. Более того, оно противоречит естественному требованию разреженности, не допуская чистых нулей в матрицах \Phi и \Theta.
  • Априорное распределение Дирихле является слишком слабым регуляризатором. Проблему неустойчивости он не решает.

Преимущества подхода АРТМ:

  • В АРТМ регуляризаторы не обязаны быть априорными распределениями и иметь какую-либо вероятностную интерпретацию.
  • Регуляризатор Дирихле утрачивает свою особую роль, его не обязательно использовать в каждой модели для всех тем.
  • Математический аппарат очень прост: чтобы добавить регуляризатор, достаточно добавить его производные в формулы М-шага.
  • Многие байесовские тематические модели (или заложенные в них идеи) удаётся переформулировать через регуляризаторы.
  • Суммируя регуляризаторы, взятые из разных моделей, можно легко строить многоцелевые комбинированные модели.
  • Тематические модели в АРТМ легче понимать, легче выводить и легче комбинировать.
  • Снижается порог вхождения в область тематического моделирования для исследователей из смежных областей.

Литература

  1. Воронцов К.В. Обзор вероятностных тематических моделей. 2018.
  2. Воронцов К. В. Аддитивная регуляризация тематических моделей коллекций текстовых документов // Доклады РАН. 2014. — Т. 455., №3. 268–271
  3. Воронцов К. В. Потапенко А. А. Регуляризация вероятностных тематических моделей для повышения интерпретируемости и определения числа тем // Компьютерная лингвистика и интеллектуальные технологии: По материалам ежегодной Международной конференции «Диалог» (Бекасово, 4–8 июня 2014 г.) Вып.13 (20). М: Изд-во РГГУ, 2014. C.676–687.
  4. Vorontsov K. V. Additive Regularization for Topic Models of Text Collections // Doklady Mathematics. 2014, Pleiades Publishing, Ltd. — Vol. 89, No. 3, pp. 301–304.
  5. Vorontsov K. V., Potapenko A. A. Tutorial on Probabilistic Topic Modeling: Additive Regularization for Stochastic Matrix Factorization // AIST’2014, Analysis of Images, Social networks and Texts. Springer International Publishing Switzerland, 2014. Communications in Computer and Information Science (CCIS). Vol. 436. pp. 29–46.
  6. Vorontsov K. V., Potapenko A. A. Additive Regularization of Topic Models // Machine Learning Journal. Special Issue “Data Analysis and Intelligent Optimization with Applications”. Русский перевод

См. также

Источник — «http://www.machinelearning.ru/wiki/index.php?title=%D0%90%D0%B4%D0%B4%D0%B8%D1%82%D0%B8%D0%B2%D0%BD%D0%B0%D1%8F_%D1%80%D0%B5%D0%B3%D1%83%D0%BB%D1%8F%D1%80%D0%B8%D0%B7%D0%B0%D1%86%D0%B8%D1%8F_%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D1%85_%D0%BC%D0%BE%D0%B4%D0%B5%D0%BB%D0%B5%D0%B9»
Личные инструменты