SVM для линейно разделимой выборки (пример)
Материал из MachineLearning.
(Содержимое страницы заменено на « {{Задание|Алексей Морозов|В.В.Стрижов|28 мая 2010}} [[Категория:Учебные матер...») |
(→Исходный код) |
||
| (54 промежуточные версии не показаны) | |||
| Строка 1: | Строка 1: | ||
| + | [[Изображение:Svm_with_margin.png|thumb|right|Пример разделения двух классов полосой максимальной ширины.]] | ||
| + | '''[[Машина опорных векторов]] (SVM — support vector machines)''' — группа алгоритмов классификации, основанных на обучении с учителем, использующих линейное разделение объектов в пространстве признаков с помощью гиперплоскости. Метод применяется для решения задачи бинарной классификации. Основной проблемой метода является выбор оптимальной гиперплоскости, которая позволяет разделить классы с максимальной точностью. Для этого разделяющая гиперплоскость должна быть выбрана таким образом, чтобы расстояние между ближайшими точками, расположенными по разные стороны от нее, было бы максимальным. Данное расстояние называется зазором (margin), а сами точки – опорными векторами (support vectors). Тогда разделяющая гиперплоскость должна быть выбрана таким образом, чтобы максимизировать зазор, что обеспечит более уверенное разделение классов. | ||
| - | |||
| - | [[Категория: | + | В данной статье приведен пример решения этой задачи для линейно разделимой выборки. Также исследуется устойчивость алгоритма: зависимость параметров разделяющей гиперплоскости от дисперсии случайной переменной. |
| + | |||
| + | == Постановка задачи линейной классификации == | ||
| + | |||
| + | Рассматривается задача обучения по прецедентам <tex>\left \langle X,\ Y,\ y*,\ X^\ell \right \rangle</tex> - , где <tex>X</tex> - пространство объектов, <tex>Y</tex> - множество ответов, <tex>y*:\ X \rightarrow Y</tex> - целевая зависимость, значения которой известны только на объектах обучающей выборки <tex>X=\(x_i,y_i\)_{i=1}^\ell\ ,\ y_i = y*(x_i)</tex>. Требуется построить алгоритм <tex>a:\ X \rightarrow Y</tex>, аппроксимирующий целевую | ||
| + | зависимость на всём пространстве <tex>X</tex>. | ||
| + | |||
| + | Требуется построить задачу классификации на два непересекающихся класса, в которой объекты описываются n-мерными вещественными векторами:<tex>\ X\ =\ \mathbb{R}^n,\ Y\ =\ \{-1,+1\}</tex>. | ||
| + | |||
| + | Будем строить линейный пороговый классификатор: | ||
| + | ::<tex>a(x)\ =\ sign(\sum_{j=1}^n w_jx^j\ -\ w_0)\ =\ sign(<w,x>\ -\ w_0)</tex>, | ||
| + | где <tex>x\ =\ (x^1,...,x^n)</tex> - признаковое описание объекта <tex>x</tex>; вектор <tex>w\ =\ (w^1,...,w^n)\ \in\ \mathbb{R}</tex> и скалярный порог <tex>w_0\ \in\ \mathbb{R}</tex> являются параметрами алгоритма. | ||
| + | |||
| + | Уравнение <tex><w,x>\ =\ w_0</tex> описывает гиперплоскость, разделяющую классы в пространстве <tex>\mathbb{R}^n</tex>. | ||
| + | |||
| + | == Описание алгоритма == | ||
| + | === Понятие оптимальной разделяющей гиперплоскости === | ||
| + | |||
| + | |||
| + | Предположим, что выборка <tex>X=\(x_i,y_i\)_{i=1}^\ell\</tex> линейно разделима. Тогда существуют значения параметров <tex>w,\ w_0</tex>, при которых функционал числа ошибок | ||
| + | ::<tex>Q(w,w_0)\ =\ \sum_{i=1}^\ell [y_i(<w,x_i>\ -\ w_0)\ <\ 0]</tex> | ||
| + | |||
| + | принимает нулевое значение. Но тогда разделяющая гиперплоскость не единственна. Можно выбрать другие её положения, реализующие такое же разбиение выборки на два класса. Идея метода заключается в том, чтобы разумным образом распорядиться этой свободой выбора. | ||
| + | |||
| + | Потребуем, чтобы разделяющая гиперплоскость максимально далеко отстояла от ближайших к ней точек обоих классов. Первоначально данный принцип классификации возник из эвристических соображений: вполне естественно полагать, что максимизация зазора между классами должна способствовать более надёжной классификации. | ||
| + | |||
| + | Заметим, что параметры линейного порогового классификатора определены с точностью до нормировки: алгоритм <tex>a(x)</tex> не изменится, если <tex>w</tex> и <tex>w_0</tex> одновременно умножить на одну и ту же положительную константу. Удобно выбрать эту константу таким образом, чтобы для всех пограничных (т. е. ближайших к разделяющей гиперплоскости) объектов <tex>x_i</tex> из <tex>X^\ell</tex> выполнялись условия ::<tex><w,x_i>\ -\ w_0\ =\ y_i</tex>. | ||
| + | |||
| + | Сделать это возможно, поскольку при оптимальном положении разделяющей гиперплоскости все пограничные объекты находятся от неё на одинаковом расстоянии. | ||
| + | Остальные объекты находятся дальше. Таким образом, для всех <tex>x_i\ \in\ X^\ell</tex> | ||
| + | {{eqno|1}} | ||
| + | <tex><w,x_i> - w_0 | ||
| + | \begin{cases} | ||
| + | \le -1, & \mbox{if }y_i=-1; \\ | ||
| + | \ge 1, & \mbox{if }y_i=+1. | ||
| + | \end{cases} | ||
| + | </tex> | ||
| + | |||
| + | Условие <tex>-1\ <\ \left \Big\langle w,x \right \Big\rangle -w_0<\ 1\ </tex> задаёт полосу, разделяющую классы. Ширина полосы, как не сложно показать, равна <tex>\frac{2}{||w||}</tex>. Она максимальна, когда норма вектора <tex>w</tex> минимальна. | ||
| + | |||
| + | === Линейно разделимая выборка === | ||
| + | Построение оптимальной разделяющей гиперплоскости сводится к минимизации квадратичной формы при <tex>\ell</tex> ограничениях-неравенствах вида {{eqref|1}} относительно <tex>n+1</tex> переменных <tex>w,\ w_0:</tex> | ||
| + | ::<tex>\left{<w,w>\rightarrow min\\y_i(<w,x_i>-w_0)\ge1,\qquad i=1,...,\ell\\ \right.</tex> | ||
| + | |||
| + | Используя аппарат функций Лагранжа, перейдем к решению двойственной задаче. Несложно показать эквивалентность этой задачи и следующей: | ||
| + | ::<tex>\left{-\mathcal{L}(\lambda)=-\sum\limits_{i=1}^\ell\lambda_i+\frac{1}{2}\sum\limits_{i=1}^\ell\sum\limits_{j=1}^\ell\lambda_i\lambda_jy_iy_j(<x_i,x_j>)\rightarrow \min\limits_\lambda \\ \lambda_i\ge 0\quad, i=1,...,\ell\\ \sum\limits_{i=1}^\ell\lambda_iy_i=0\quad\right. </tex> | ||
| + | |||
| + | Вектор весов будем искать в ввиде <tex>w = \sum\limits_{i=1}^l\lambda_ix_iy_i</tex>. Для определения порога <tex>w_0</tex> достаточно взять произвольный опорный вектор <tex>x_i</tex> и выразить <tex>w_0</tex> из равенства <tex>w_0=<w,x_i>-y_i</tex>. На практике для повышения численной устойчивости лучше взять в качестве <tex>w_0</tex> медиану: <tex>w_0=med\{<w_i,x_i>-y_i:\ \lambda_i>0,\ i=1,...,\ell\}</tex>. Параметры полосы найдены и можно строить разделяюую полосу. | ||
| + | |||
| + | |||
| + | |||
| + | == Вычислительный эксперимент == | ||
| + | |||
| + | Вычислительный экстперимент разбит на три частей: | ||
| + | ::1. Нормальное распределение выборки; | ||
| + | ::2. Реализация алгоритма SVM для линейно разделимой выборки; | ||
| + | ::3. Исследование устойчивости алгоритма SVM; | ||
| + | |||
| + | === Нормальное распределение выборки === | ||
| + | |||
| + | Нормальным случайным распределением генерируются два класса обьектов по 10 обьектов в каждом классе. | ||
| + | [[Изображение:Normal distribution.png|1000px]] | ||
| + | |||
| + | === Реализация алгоритма SVM для линейно разделимой выборки === | ||
| + | В ходе вычислений определяются параметры раздляющей полосы. Классы линейно разделимы и ширина зазора максимальна, как видно на рисунке снизу. | ||
| + | |||
| + | [[Изображение:Classified classes example.png|1000px]] | ||
| + | |||
| + | Но алгоритм не очень хорош тем, что очень чувствителен к выбросам | ||
| + | [[Изображение:Outlier example.png|1000px]] | ||
| + | |||
| + | === Исследование устойчивости алгоритма SVM === | ||
| + | В этой части вычислительного эксперимента исследуется зависимость параметров разделяющей прямой и среднеквадратичного отклонения параметров разделяющей прямой от среднеквадратичного отклонения выборки. Параметры разделяющей гипперплоскости на графике w_0,w_1 и w_2. Как можем видеть, с увеличением среднеквадратичного отклонения выборки параметры прямой сильно колеблются. | ||
| + | [[Изображение:Stability of SVM.png|1000px]] | ||
| + | |||
| + | === Удаление шумовых выбросов алгоритма SVM === | ||
| + | Опишем алгоритм по которому будем избавляться от выбросов: | ||
| + | |||
| + | 1. Проверяем, можно ли разделить все точки исходной выборки на два класса, так чтобы точки первого класса были по одну сторону от прямой, а точки второго класса по другую сторону. Если можем разделить, то строим эту плоскость и заканчиваем алгоритм. Иначе идем в пункт 2.; | ||
| + | |||
| + | 2. Выбираем случайным образом по половине точек из каждого класса исходной выборки. Проверяем, можно ли разделить все точки новой выборки на два класса по алгоритму из пункта 1.; Если можем, то получаем параметры новой разделяющей прямой и идем в пункт 3. Иначе повторяем пункт 2.; | ||
| + | |||
| + | 3. Находим все неправильно классифицированные точки относительно новой прямой. Все неправильно классифицированные точки ранжируем по расстоянию от них до новой разделяющей прямой. Отбрасываем половину неправильно классифицированных точек из исходной выборки. Идем в пункт 1. | ||
| + | |||
| + | |||
| + | |||
| + | Сгенерировали случайную выборку из двух классов. Видно что линейно она неразделимая. | ||
| + | [[Изображение:Training_sample.png|1000px]] | ||
| + | |||
| + | Использовав алгоритм удаления выбросов получаем линейно разделимую выборку. | ||
| + | [[Изображение:Classified_sample.png|1000px]] | ||
| + | |||
| + | Математические ожидания обоих классов равны (1,1) и (4,4) соответственно. Среднеквадратичное отклонение обоих классов равно (3,3). | ||
| + | Из графика видно что, классы разделены качественно. | ||
| + | |||
| + | == Исходный код == | ||
| + | Код MATLAB можно скачать здесь: [https://mlalgorithms.svn.sourceforge.net/svnroot/mlalgorithms/Group774/Morozov2010SVMLinear/] | ||
| + | |||
| + | == Смотри также == | ||
| + | * [[ Машина опорных векторов ]] | ||
| + | * [[ Линейный классификатор ]] | ||
| + | * [[ Численные методы обучения по прецедентам (практика, В.В. Стрижов) ]] | ||
| + | * [[ SVM для линейно неразделимой выборки (пример) ]] | ||
| + | |||
| + | == Литература == | ||
| + | * Вапник В.Н., Червоненкис А.Я. Теория распознавания образов. Статистические проблемы обучения. - Москва, "Наука", 1974. | ||
| + | * Cortes C., Vapnik V. Support Vector Networks. | ||
| + | |||
| + | {{ЗаданиеВыполнено|Алексей Морозов|В.В.Стрижов|28 мая 2010|MORAL|Strijov}} | ||
| + | [[Категория:Практика и вычислительные эксперименты]] | ||
[[Категория:Классификация]] | [[Категория:Классификация]] | ||
[[Категория:Линейные классификаторы]] | [[Категория:Линейные классификаторы]] | ||
Текущая версия
Машина опорных векторов (SVM — support vector machines) — группа алгоритмов классификации, основанных на обучении с учителем, использующих линейное разделение объектов в пространстве признаков с помощью гиперплоскости. Метод применяется для решения задачи бинарной классификации. Основной проблемой метода является выбор оптимальной гиперплоскости, которая позволяет разделить классы с максимальной точностью. Для этого разделяющая гиперплоскость должна быть выбрана таким образом, чтобы расстояние между ближайшими точками, расположенными по разные стороны от нее, было бы максимальным. Данное расстояние называется зазором (margin), а сами точки – опорными векторами (support vectors). Тогда разделяющая гиперплоскость должна быть выбрана таким образом, чтобы максимизировать зазор, что обеспечит более уверенное разделение классов.
В данной статье приведен пример решения этой задачи для линейно разделимой выборки. Также исследуется устойчивость алгоритма: зависимость параметров разделяющей гиперплоскости от дисперсии случайной переменной.
Содержание |
Постановка задачи линейной классификации
Рассматривается задача обучения по прецедентам - , где
- пространство объектов,
- множество ответов,
- целевая зависимость, значения которой известны только на объектах обучающей выборки
. Требуется построить алгоритм
, аппроксимирующий целевую
зависимость на всём пространстве
.
Требуется построить задачу классификации на два непересекающихся класса, в которой объекты описываются n-мерными вещественными векторами:.
Будем строить линейный пороговый классификатор:
,
где - признаковое описание объекта
; вектор
и скалярный порог
являются параметрами алгоритма.
Уравнение описывает гиперплоскость, разделяющую классы в пространстве
.
Описание алгоритма
Понятие оптимальной разделяющей гиперплоскости
Предположим, что выборка линейно разделима. Тогда существуют значения параметров
, при которых функционал числа ошибок
принимает нулевое значение. Но тогда разделяющая гиперплоскость не единственна. Можно выбрать другие её положения, реализующие такое же разбиение выборки на два класса. Идея метода заключается в том, чтобы разумным образом распорядиться этой свободой выбора.
Потребуем, чтобы разделяющая гиперплоскость максимально далеко отстояла от ближайших к ней точек обоих классов. Первоначально данный принцип классификации возник из эвристических соображений: вполне естественно полагать, что максимизация зазора между классами должна способствовать более надёжной классификации.
Заметим, что параметры линейного порогового классификатора определены с точностью до нормировки: алгоритм не изменится, если
и
одновременно умножить на одну и ту же положительную константу. Удобно выбрать эту константу таким образом, чтобы для всех пограничных (т. е. ближайших к разделяющей гиперплоскости) объектов
из
выполнялись условия ::
.
Сделать это возможно, поскольку при оптимальном положении разделяющей гиперплоскости все пограничные объекты находятся от неё на одинаковом расстоянии.
Остальные объекты находятся дальше. Таким образом, для всех
Условие задаёт полосу, разделяющую классы. Ширина полосы, как не сложно показать, равна
. Она максимальна, когда норма вектора
минимальна.
Линейно разделимая выборка
Построение оптимальной разделяющей гиперплоскости сводится к минимизации квадратичной формы при ограничениях-неравенствах вида (1) относительно
переменных
Используя аппарат функций Лагранжа, перейдем к решению двойственной задаче. Несложно показать эквивалентность этой задачи и следующей:
Вектор весов будем искать в ввиде . Для определения порога
достаточно взять произвольный опорный вектор
и выразить
из равенства
. На практике для повышения численной устойчивости лучше взять в качестве
медиану:
. Параметры полосы найдены и можно строить разделяюую полосу.
Вычислительный эксперимент
Вычислительный экстперимент разбит на три частей:
- 1. Нормальное распределение выборки;
- 2. Реализация алгоритма SVM для линейно разделимой выборки;
- 3. Исследование устойчивости алгоритма SVM;
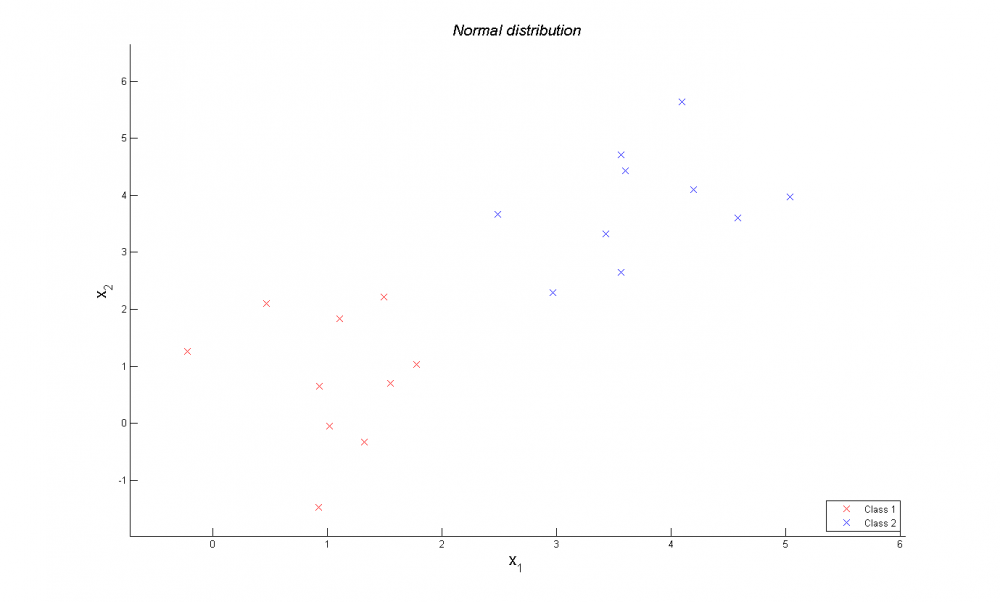
Нормальное распределение выборки
Нормальным случайным распределением генерируются два класса обьектов по 10 обьектов в каждом классе.
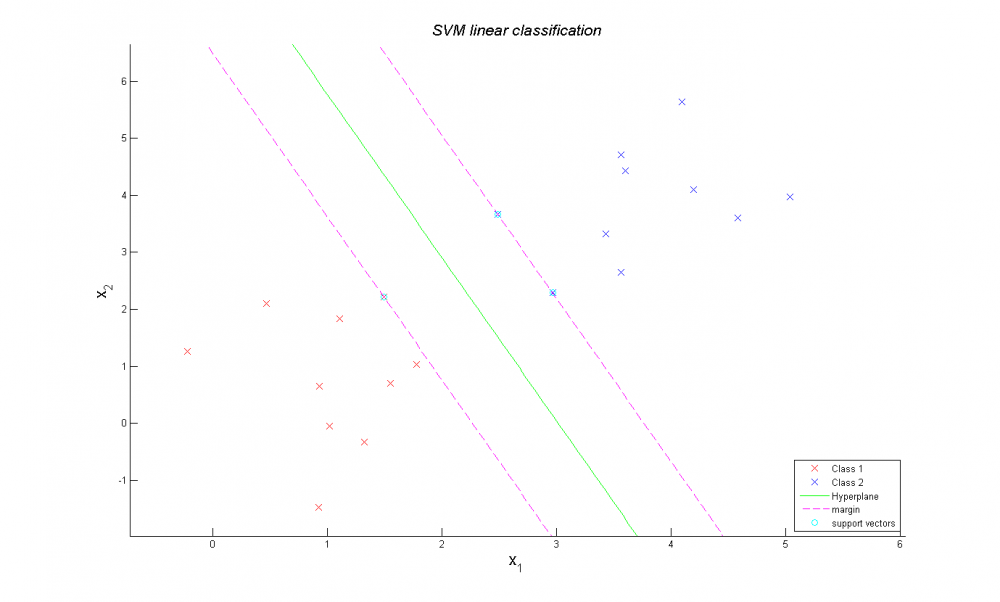
Реализация алгоритма SVM для линейно разделимой выборки
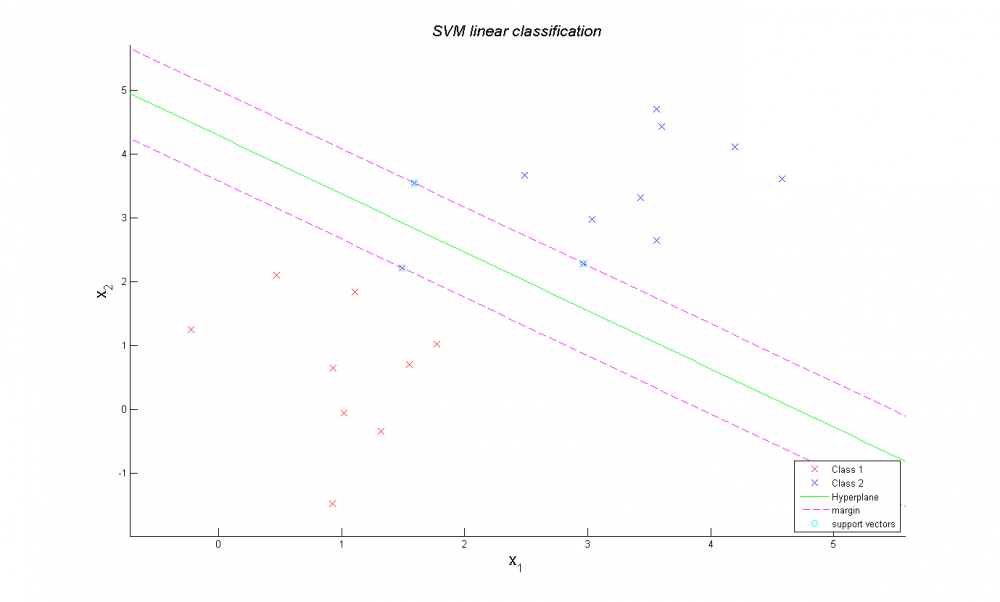
В ходе вычислений определяются параметры раздляющей полосы. Классы линейно разделимы и ширина зазора максимальна, как видно на рисунке снизу.
Но алгоритм не очень хорош тем, что очень чувствителен к выбросам
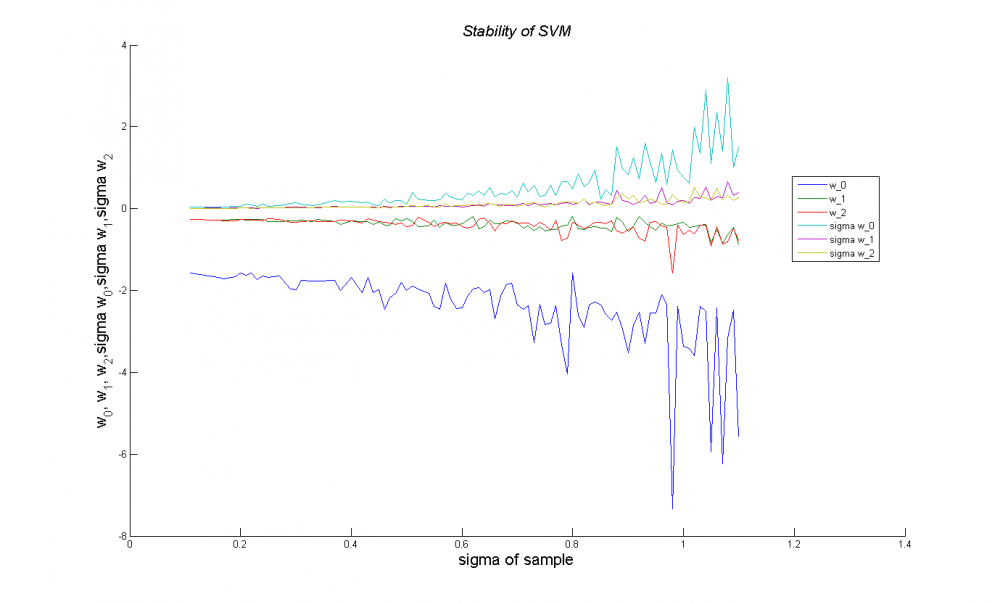
Исследование устойчивости алгоритма SVM
В этой части вычислительного эксперимента исследуется зависимость параметров разделяющей прямой и среднеквадратичного отклонения параметров разделяющей прямой от среднеквадратичного отклонения выборки. Параметры разделяющей гипперплоскости на графике w_0,w_1 и w_2. Как можем видеть, с увеличением среднеквадратичного отклонения выборки параметры прямой сильно колеблются.
Удаление шумовых выбросов алгоритма SVM
Опишем алгоритм по которому будем избавляться от выбросов:
1. Проверяем, можно ли разделить все точки исходной выборки на два класса, так чтобы точки первого класса были по одну сторону от прямой, а точки второго класса по другую сторону. Если можем разделить, то строим эту плоскость и заканчиваем алгоритм. Иначе идем в пункт 2.;
2. Выбираем случайным образом по половине точек из каждого класса исходной выборки. Проверяем, можно ли разделить все точки новой выборки на два класса по алгоритму из пункта 1.; Если можем, то получаем параметры новой разделяющей прямой и идем в пункт 3. Иначе повторяем пункт 2.;
3. Находим все неправильно классифицированные точки относительно новой прямой. Все неправильно классифицированные точки ранжируем по расстоянию от них до новой разделяющей прямой. Отбрасываем половину неправильно классифицированных точек из исходной выборки. Идем в пункт 1.
Сгенерировали случайную выборку из двух классов. Видно что линейно она неразделимая.
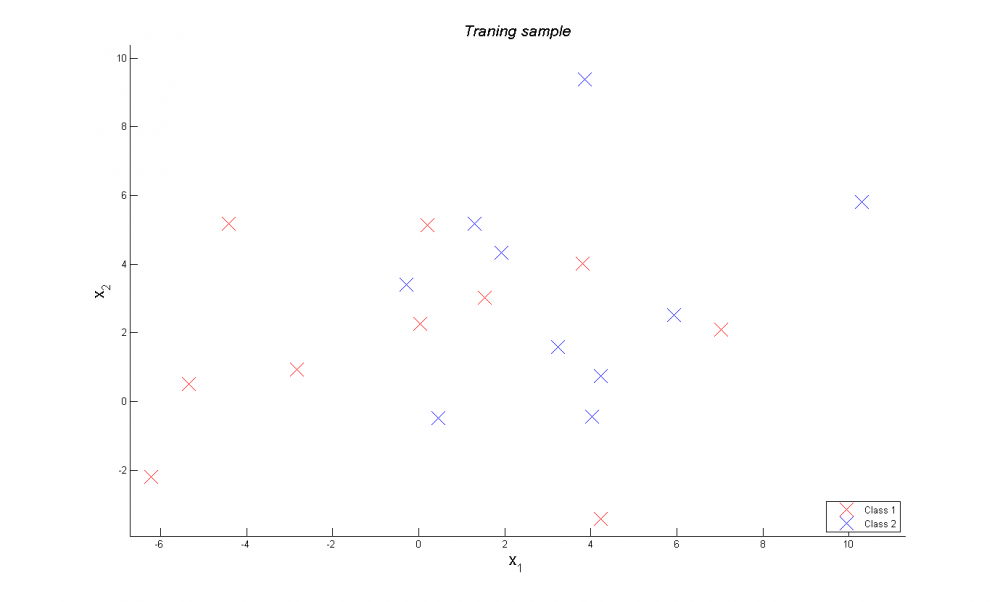
Использовав алгоритм удаления выбросов получаем линейно разделимую выборку.
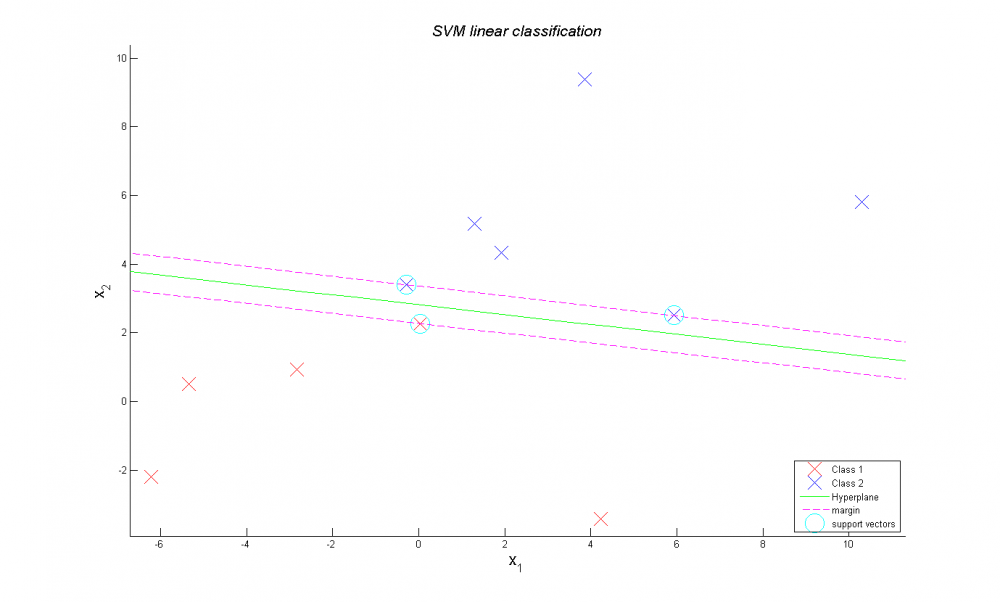
Математические ожидания обоих классов равны (1,1) и (4,4) соответственно. Среднеквадратичное отклонение обоих классов равно (3,3). Из графика видно что, классы разделены качественно.
Исходный код
Код MATLAB можно скачать здесь: [1]
Смотри также
- Машина опорных векторов
- Линейный классификатор
- Численные методы обучения по прецедентам (практика, В.В. Стрижов)
- SVM для линейно неразделимой выборки (пример)
Литература
- Вапник В.Н., Червоненкис А.Я. Теория распознавания образов. Статистические проблемы обучения. - Москва, "Наука", 1974.
- Cortes C., Vapnik V. Support Vector Networks.
| | Данная статья была создана в рамках учебного задания.
См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе. |