Анализ регрессионных остатков (пример)
Материал из MachineLearning.
(→Исходный код) |
|||
| (69 промежуточных версий не показаны.) | |||
| Строка 1: | Строка 1: | ||
| - | Для получения информации об адекватности построенной модели многомерной линейной регрессии используется '''[[анализ регрессионных остатков]]''' | + | {{TOCright}} |
| + | Для получения информации об адекватности построенной модели многомерной линейной регрессии используется '''[[анализ регрессионных остатков]]'''. | ||
== Постановка задачи == | == Постановка задачи == | ||
| Строка 5: | Строка 6: | ||
<tex>y_i=\sum_{j=1}^m w_j x_{ij} + \varepsilon_i, i=1,\dots,n</tex>. Требуется создать инструмент анализа адекватности модели используя '''[[анализ регрессионных остатков]]''' и исследовать значимость признаков и поведение остатков в случае гетероскедастичности. | <tex>y_i=\sum_{j=1}^m w_j x_{ij} + \varepsilon_i, i=1,\dots,n</tex>. Требуется создать инструмент анализа адекватности модели используя '''[[анализ регрессионных остатков]]''' и исследовать значимость признаков и поведение остатков в случае гетероскедастичности. | ||
| + | |||
== Описание алгоритма == | == Описание алгоритма == | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | Для проверки | + | === Анализ регрессионных остатков === |
| - | Для | + | Анализ регрессионных остатков заключается в проверке нескольких гипотез: |
| + | * <tex> E \varepsilon_i = 0,i= 1,\dots,n</tex>{{eqno|1}} | ||
| + | * <tex> D \varepsilon_i = \sigma^2,i= 1,\dots,n</tex>{{eqno|2}} | ||
| + | * <tex> \varepsilon_i \sim N(0,\sigma), i= 1,\dots,n</tex> {{eqno|3}} | ||
| + | * <tex> \varepsilon_i, i= 1,\dots,n</tex>{{eqno|4}} — независимы | ||
| + | где <tex>\varepsilon_i=y_i - f_i</tex>, <tex>i= 1,\dots,n</tex>, — регрессионные остатки конкретной модели. <tex>f_i</tex> - отклики посчитанные по модели, а <tex>y_i</tex> - эмпирические отклики. | ||
| + | |||
| + | Для проверки первой гипотезы воспользуемся [[критерий знаков|критерием знаков]]. | ||
| + | Проверка второй гипотезы, по сути, является проверкой на гомоскедастичность, то есть на постоянство дисперсии, случай гетероскедастичности будет рассмотрен ниже. Для этого воспользуемся двумя статистическими тестами: тестом Ансари-Брэдли и критерием Голдфелда-Кванта. | ||
| + | Так как тест Ансари-Брэдли фактически осуществляет проверку гипотезы, что у двух предоставленных выборок дисперсии одинаковы, а мы фактически имеем только один вектор остатков, то произведем несколько тестов, сравнивая в каждом две случайные выборки из нашего вектора остатков. | ||
| + | Проверку нормальности распределения осуществим с помощью [[критерий хи-квадрат|критерия согласия хи-квадрат]], модифицированного для проверки на нормальность, то есть сравнивая данное нам распределение в остатках с нормальным распределением, имеющим моментные характеристики, вычисленные из вектора остатков. Наконец, проверку последнего условия реализуем с помощью [[статистика Дарбина-Уотсона|статистики Дарбина-Уотсона]]. | ||
| + | |||
| + | === Оценка значимости признаков === | ||
| + | Задача состоит в проверке для каждого из признаков, дает ли нам учет этого признака в модели более хорошие результаты, нежели его отсутствие. Оценивать результаты будем с помощью [[коэффициент детерминации|коэффициента детерминации]]: | ||
| + | |||
| + | <tex>R^2 \equiv 1 - {\sum_i (y_i - {f}_i)^2\over \sum_i (y_i-\bar{y})^2\,</tex> | ||
| + | |||
| + | где <tex>y_i</tex> — эмпирический отклик, <tex>f_i</tex> — отклик, посчитанный по модели, и | ||
| + | <tex>\bar{y}</tex> — [[математическое ожидание]] <tex>y_i</tex>. | ||
| + | |||
| + | == Гетероскедастичность == | ||
| + | Термин гетероскедастичность применяется в ситуации, когда ошибки в различных наблюдениях некоррелированы, но их дисперсии — разные. Соответственно термин гомоскедастичность применяется в случае постоянных дисперсий. | ||
| + | |||
| + | === Визуальный анализ === | ||
| + | Одним из основных методов предварительного исследования на гетероскедастичность является визуальный анализ графика остатков. Целью данного анализа является нахождение факторов влияющих на изменение дисперсии, номер измерения или значение одного из признаков. Для сравнения приведем несколько примеров. | ||
| + | |||
| + | [[Изображение:homo.png|600px]] | ||
| + | |||
| + | Выше представлена госмоскедастичная модель. Действительно, используя визуальный анализ, не получается найти какие-то признаки непостоянства дисперсии и тем более какие-то зависимости. | ||
| + | |||
| + | [[Изображение:hetero1.png|600px]] | ||
| + | |||
| + | В данном случае визуально можно констатировать факт непостоянства дисперсии и даже связать это изменение с номером эксперимента (или возможно с одним из признаков, если он монотонно изменялся по номеру эксперимента). | ||
| + | |||
| + | [[Изображение:hetero2.png|600px]] | ||
| + | |||
| + | Еще один пример визуально определимой гетероскедастичности. | ||
| + | |||
| + | === Статистические методы детекции === | ||
| + | Опишем суть нескольких общеупотребительных статистических тестов на гетероскедастичность. | ||
| + | Во всех этих тестах основной гипотезой <tex>H_0</tex> является равенство <tex>\sigma_1^2=\sigma_2^2=\dots=\sigma_n^2</tex> против альтернативной гипотезы <tex>H_1</tex>: не <tex>H_0</tex>. | ||
| + | |||
| + | ==== Тест Уайта ==== | ||
| + | Содержательный смысл теста в том, что часто гетероскедастичность модели вызвана зависимостью (возможно довольно сложной) дисперсий ошибок от признаков. Реализуя эту идею, Уайт предложил метод тестирования гипотезы <tex>H_0</tex> без каких-либо предположений о структуре гетероскедастичности. Сначала к исходной модели применяется обычный [[метод наименьших квадратов]] и находятся остатки регрессии <tex>e_t, t=1,\dots\,n</tex>. Затем осуществляется регрессия квадратов этих остатков <tex>e_t^2</tex> на все признаки, их квадраты, попарные произведения и константу. | ||
| + | Тогда при гипотезе <tex>H_0</tex> величина <tex>nR^2</tex> асимптотически имеет распределение <tex>\chi^2(N-1)</tex>, где <tex>R^2</tex> — [[коэффициент детерминации]], а <tex>N</tex> — число регрессоров второй регрессии. | ||
| + | Плюс данного теста — его универсальность. Минусы : 1) если гипотеза <tex>H_0</tex> отвергается, то никаких указаний на функциональную форму гетероскедастичности мы не получаем; 2) несомненным минусом является поиск вслепую вида регрессии(начинаем приближать простыми полиномами второй степени без какой бы то ни было причины на это) | ||
| + | |||
| + | ====Тест Голдфелда-Кванта==== | ||
| + | Этот тест применяется, когда есть предположение о прямой зависимости дисперсии ошибок от некоторого признака. Алгоритм метода: | ||
| + | # упорядочить данные по убыванию того признака, относительно которого сделано предположение; | ||
| + | # Делим наблюдения на три части, причём они должны быть равны или примерно равны, а также первая и третья должны быть одинаковы. | ||
| + | # Провести две независимые регрессии для первой части и для последней. Рассчитать выровненные значения и построить соответствующие остатки (<tex>y_{vyr} -y</tex>):<tex>e_1</tex> и <tex>e_2</tex>; | ||
| + | # Cоставить [[критерий Фишера | cтатистику Фишера]] <tex>F=(\sum(e_1)^2)/(\sum(e_2)^2</tex>. Если <tex>F>F</tex>кр, следовательно есть гетероскедостичность. | ||
| + | |||
| + | ====Тест Ансари-Брэдли==== | ||
| + | Тест получает на вход две выборки размеров <tex>n_1</tex> и <tex>n_2</tex> и проверяет на равенство дисперсий распределения, из которых они могли быть получены. Алгоритм метода пошагово: | ||
| + | * Расположим <tex>n = n_1 + n_2</tex> по возрастанию; | ||
| + | * Расставим метки таким образом : <tex>(n_1+n_2)/2 , (n_1+n_2)/2 - 1, \dots ,2,1,1,2, \dots , (n_1+n_2)/2 - 1, (n_1+n_2)/2</tex> | ||
| + | |||
| + | ===Эвристика=== | ||
| + | Суть данной эвристики состоит в ранжировании псевдодисперсий и в анализе полученной гистограммы. Под псевдодисперсией будем понимать величины | ||
| + | <tex> dis_i = \varepsilon_i^2 - mean^2</tex>, где <tex>mean = \sum_{i=1}^n \varepsilon_i/n</tex>. Простейший анализ гистограммы, состоящей из 10 интервалов, будем проводить сравнением количества элементов на первых двух интервалах. Это отношение будем сравнивать с некоторой, заранее заданной константой, на основе чего и будем принимать решение о гетероскедастичности. Вот пример гистограммы для гомоскедастичного случая (график его остатков был представлен ранее): | ||
| + | |||
| + | [[image:hist.png]] | ||
| + | |||
| + | Легко заметить, что порядок отношения первых двух столбцов - около пяти-шести к одному, что же касается гетероскедастичного случая, это отношение будет больше семи (было замечено вплоть до 34) примеры можно посмотреть ниже, в вычислительном эксперименте. | ||
| + | |||
| + | == Вычислительный эксперимент на модельных данных == | ||
| + | |||
| + | В данном отчете представлены результаты применения созданного инструмента анализа представленной модели с помощью исследования ее регрессионных остатков. Отчет состоит из трех экспериментов, демонстрирующих плюсы и минусы созданного инструмента. | ||
| + | |||
| + | |||
| + | === Три модели === | ||
| + | |||
| + | Представленные модели были подобраны так, чтобы визуальный анализ регрессионных остатков не давал очевидных результатов. Будем проводить исследование в два этапа - вначале проверяя модель на выполнение основных гипотез, затем исследуя модель на гетероскедастичность с помощью теста Голдфелда-Кванта и несложной эвристики. | ||
| + | |||
| + | ==== Модель №1 (хорошая) ==== | ||
| + | |||
| + | Наша модель : <tex>y_i=\sum_{j=1}^m w_j x_{ij} + \varepsilon_i, i=1,\dots,n</tex>, где <tex>\varepsilon_i \sim N(0,\sigma), i= 1,\dots,n</tex>. Таким образом все гипотезы должны выполняться и гетероскедастичность должна отсутствовать. | ||
| + | |||
| + | <big>[A,x,res] = GetGoodExample | ||
| + | [meanst, distab, normchi2, normjb] = ResAnalysis(res) | ||
| + | GoldfeldQuandt(A(:,1:end-1),A(:,end),1) | ||
| + | GoldfeldQuandt(A(:,1:end-1),A(:,end),2) | ||
| + | HistAnalys(res)</big> | ||
| + | |||
| + | |||
| + | Получаем результат: | ||
| + | |||
| + | <big>% Проверка основных гипотез | ||
| + | meanst = 0 | ||
| + | distab = 0.0500 | ||
| + | normchi2 = 0 | ||
| + | normjb = 0 | ||
| + | %Проверка на гетероскедастичность% | ||
| + | goldfeldquandt1 = 0 | ||
| + | goldfeldquandt2 = 0 | ||
| + | result = 0</big> | ||
| + | |||
| + | |||
| + | График остатков этой модели уже был приведен выше и не представляет особого интереса. | ||
| + | |||
| + | ==== Модель №2 (плохая, одномерная) ==== | ||
| + | |||
| + | Наша модель : <tex>y_i=w*x_i + sin(x_i)\varepsilon_i, i=1,\dots,n</tex>, где <tex>\varepsilon_i \sim N(0,\sigma), i= 1,\dots,n</tex>. Таким образом, модель очевидным образом гетероскедастична, но визуальным анализом это сложно обнаружить(см.рисунок). | ||
| + | |||
| + | [[image:bad.png]] | ||
| + | |||
| + | <big>[A,x,res] = GetBadExample | ||
| + | [meanst, distab, normchi2, normjb] = ResAnalysis(res) | ||
| + | GoldfeldQuandt(A(:,1:end-1),A(:,end),1) | ||
| + | HistAnalys(res)</big> | ||
| + | |||
| + | |||
| + | Получаем результат: | ||
| + | |||
| + | <big>% Проверка основных гипотез | ||
| + | meanst = 0 | ||
| + | distab = 0.0340 | ||
| + | normchi2 = 1.0020 | ||
| + | normjb = 1.0020 | ||
| + | %Проверка на гетероскедастичность% | ||
| + | goldfeldquandt1 = 0 | ||
| + | result = 1</big> | ||
| + | |||
| + | |||
| + | Нормальность отвергнута. Гетероскедастичность была обнаружена только эвристикой. Приведем гистограмму полученную эвристикой: | ||
| + | |||
| + | [[image:badhist.png]] | ||
| + | |||
| + | ==== Модель №3 (плохая,многомерная) ==== | ||
| + | |||
| + | Наша модель : <tex>y_i=\sum_{j=1}^m w_j x_{ij} + ((x_1)^2+x_2)\varepsilon_i, i=1,\dots,n</tex>, где <tex>\varepsilon_i \sim N(0,\sigma), i= 1,\dots,n</tex>. Таким образом, модель очевидным образом гетероскедастична, но снова визуальным анализом это сложно обнаружить(см.рисунок). | ||
| + | |||
| + | [[image:bad1.png]] | ||
| + | |||
| + | <big> | ||
| + | [A,x,res] = GetBadExample1 | ||
| + | [meanst, distab, normchi2, normjb] = ResAnalysis(res) | ||
| + | GoldfeldQuandt(A(:,1:end-1),A(:,end),1) | ||
| + | GoldfeldQuandt(A(:,1:end-1),A(:,end),2) | ||
| + | GoldfeldQuandt(A(:,1:end-1),A(:,end),5) | ||
| + | HistAnalys(res)</big> | ||
| + | |||
| + | |||
| + | Получаем результат: | ||
| + | |||
| + | <big>% Проверка основных гипотез | ||
| + | meanst = 0 | ||
| + | distab = 0.0288 | ||
| + | normchi2 = 1.0025 | ||
| + | normjb = 1.0025 | ||
| + | %Проверка на гетероскедастичность% | ||
| + | goldfeldquandt1 = 1 | ||
| + | goldfeldquandt2 = 1 | ||
| + | goldfeldquandt5 = 0 | ||
| + | result = 1</big> | ||
| + | |||
| + | |||
| + | Нормальность отвергнута. Гетероскедастичность была обнаружена как эвристикой, так и тестом Голдфелда-Квандта (зависимость от первой и второй и независимость от пятой переменной). Приведем гистограмму полученную эвристикой: | ||
| + | |||
| + | [[image:badhist1.png]] | ||
| + | |||
| + | === Выводы === | ||
| + | |||
| + | Статистические проверки на нормальность показали себя с наилучшей стороны. Эвристика показала хорошие результаты в исследовании на гетероскедастичность. Тест Голдфелда-Квандта не сработал только в одном тесте. Тест Ансари-Брэдли (использовался для проверки на постоянство дисперсии) показал наихудшие результаты, так как с его помощью не удалось различить две существенно разные модели. Это вполне объяснимо: мы применяли этот тест для сравнения дисперсий двух случайных выборок взятых из нашего вектора остатков. Вполне очевидно что результат достаточно не предсказуем вследствие именно этой случайности выборок. В итоге мы получали одинаковые результаты для разных моделей. (причем увеличение числа экспериментов не решает данной проблемы). | ||
| + | |||
| + | ==Исходный код== | ||
| + | |||
| + | [https://mlalgorithms.svn.sourceforge.net/svnroot/mlalgorithms/Group774/Ivkin2010Analysis Функции анализирующие остатки (реализовано в MATLAB)] | ||
| + | |||
| + | ==См. также== | ||
| + | [http://en.wikipedia.org/wiki/Heteroscedasticity Wikipedia о гетероскедастичности, англ.] | ||
| + | |||
| + | [[Коэффициент детерминации]] | ||
| + | |||
| + | [[Анализ регрессионных остатков]] | ||
| + | |||
| + | == Литература == | ||
| + | * Н.Джонсон, Ф.Лион Статистика и планирование эксперимента в технике и науке, перевод с английского «Мир»,1980. — 610 c. | ||
| + | * Я. Р. Магнус, П. К. Катышев, А. А. Пересецкий Эконометрика. Начальный курс:Учеб. — 6 изд.,перераб.и доп. — М.:Дело,2004. — 576 с. ISBN 5-7749-0055-Х | ||
| + | * Applied Logistic Regression/ David W. Hosmer,Stanley Lemeshow.-2nd ed. -Wiley-Interscience Publication,2000. - 397 c. ISBN 0-471-35632-8 | ||
| + | * Кобзарь А. И. Прикладная математическая статистика. — М.: Физматлит, 2006. — 816 с. ISBN 5-9221-0707-0 | ||
| + | |||
| + | |||
| + | {{ЗаданиеВыполнено|Никита Ивкин|В.В.Стрижов|28 мая 2010|Nikitaivkin|strijov}} | ||
| + | [[Категория:Практика и вычислительные эксперименты]] | ||
| + | [[Категория:Регрессионный анализ]] | ||
Текущая версия
|
Для получения информации об адекватности построенной модели многомерной линейной регрессии используется анализ регрессионных остатков.
Постановка задачи
Задана выборка откликов и признаков. Рассматривается множество линейных регрессионных моделей вида:
. Требуется создать инструмент анализа адекватности модели используя анализ регрессионных остатков и исследовать значимость признаков и поведение остатков в случае гетероскедастичности.
Описание алгоритма
Анализ регрессионных остатков
Анализ регрессионных остатков заключается в проверке нескольких гипотез:
- (1)
- (2)
- (3)
- (4)— независимы
где ,
, — регрессионные остатки конкретной модели.
- отклики посчитанные по модели, а
- эмпирические отклики.
Для проверки первой гипотезы воспользуемся критерием знаков. Проверка второй гипотезы, по сути, является проверкой на гомоскедастичность, то есть на постоянство дисперсии, случай гетероскедастичности будет рассмотрен ниже. Для этого воспользуемся двумя статистическими тестами: тестом Ансари-Брэдли и критерием Голдфелда-Кванта. Так как тест Ансари-Брэдли фактически осуществляет проверку гипотезы, что у двух предоставленных выборок дисперсии одинаковы, а мы фактически имеем только один вектор остатков, то произведем несколько тестов, сравнивая в каждом две случайные выборки из нашего вектора остатков. Проверку нормальности распределения осуществим с помощью критерия согласия хи-квадрат, модифицированного для проверки на нормальность, то есть сравнивая данное нам распределение в остатках с нормальным распределением, имеющим моментные характеристики, вычисленные из вектора остатков. Наконец, проверку последнего условия реализуем с помощью статистики Дарбина-Уотсона.
Оценка значимости признаков
Задача состоит в проверке для каждого из признаков, дает ли нам учет этого признака в модели более хорошие результаты, нежели его отсутствие. Оценивать результаты будем с помощью коэффициента детерминации:
где — эмпирический отклик,
— отклик, посчитанный по модели, и
— математическое ожидание
.
Гетероскедастичность
Термин гетероскедастичность применяется в ситуации, когда ошибки в различных наблюдениях некоррелированы, но их дисперсии — разные. Соответственно термин гомоскедастичность применяется в случае постоянных дисперсий.
Визуальный анализ
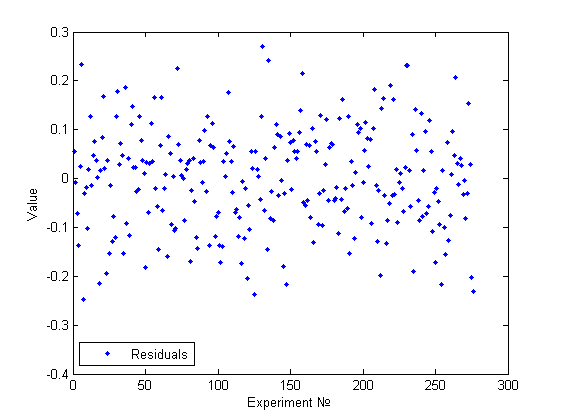
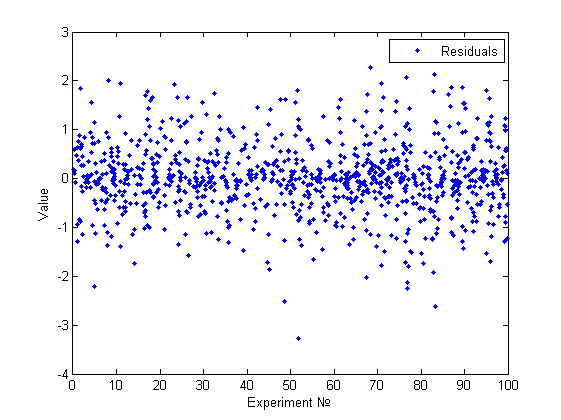
Одним из основных методов предварительного исследования на гетероскедастичность является визуальный анализ графика остатков. Целью данного анализа является нахождение факторов влияющих на изменение дисперсии, номер измерения или значение одного из признаков. Для сравнения приведем несколько примеров.
Выше представлена госмоскедастичная модель. Действительно, используя визуальный анализ, не получается найти какие-то признаки непостоянства дисперсии и тем более какие-то зависимости.
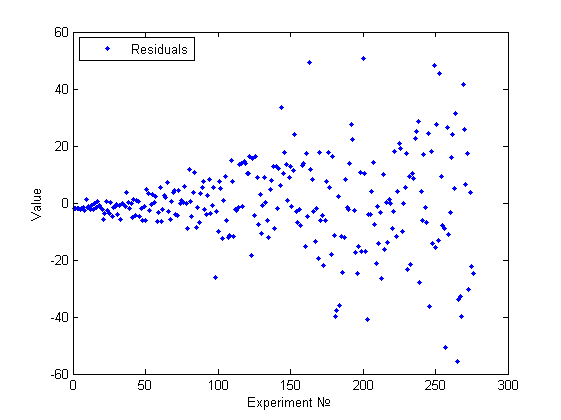
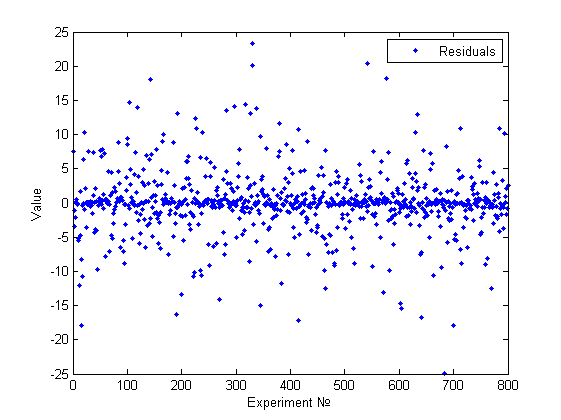
В данном случае визуально можно констатировать факт непостоянства дисперсии и даже связать это изменение с номером эксперимента (или возможно с одним из признаков, если он монотонно изменялся по номеру эксперимента).
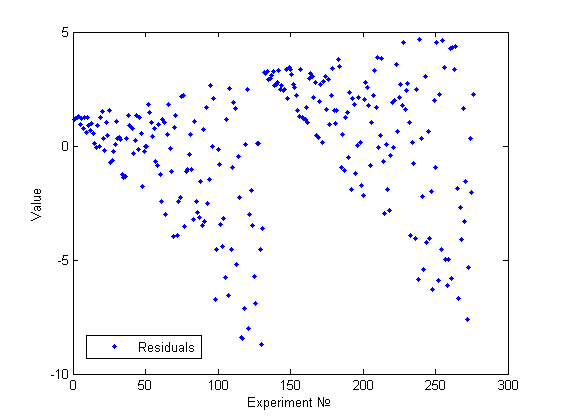
Еще один пример визуально определимой гетероскедастичности.
Статистические методы детекции
Опишем суть нескольких общеупотребительных статистических тестов на гетероскедастичность.
Во всех этих тестах основной гипотезой является равенство
против альтернативной гипотезы
: не
.
Тест Уайта
Содержательный смысл теста в том, что часто гетероскедастичность модели вызвана зависимостью (возможно довольно сложной) дисперсий ошибок от признаков. Реализуя эту идею, Уайт предложил метод тестирования гипотезы без каких-либо предположений о структуре гетероскедастичности. Сначала к исходной модели применяется обычный метод наименьших квадратов и находятся остатки регрессии
. Затем осуществляется регрессия квадратов этих остатков
на все признаки, их квадраты, попарные произведения и константу.
Тогда при гипотезе
величина
асимптотически имеет распределение
, где
— коэффициент детерминации, а
— число регрессоров второй регрессии.
Плюс данного теста — его универсальность. Минусы : 1) если гипотеза
отвергается, то никаких указаний на функциональную форму гетероскедастичности мы не получаем; 2) несомненным минусом является поиск вслепую вида регрессии(начинаем приближать простыми полиномами второй степени без какой бы то ни было причины на это)
Тест Голдфелда-Кванта
Этот тест применяется, когда есть предположение о прямой зависимости дисперсии ошибок от некоторого признака. Алгоритм метода:
- упорядочить данные по убыванию того признака, относительно которого сделано предположение;
- Делим наблюдения на три части, причём они должны быть равны или примерно равны, а также первая и третья должны быть одинаковы.
- Провести две независимые регрессии для первой части и для последней. Рассчитать выровненные значения и построить соответствующие остатки (
):
и
;
- Cоставить cтатистику Фишера
. Если
кр, следовательно есть гетероскедостичность.
Тест Ансари-Брэдли
Тест получает на вход две выборки размеров и
и проверяет на равенство дисперсий распределения, из которых они могли быть получены. Алгоритм метода пошагово:
- Расположим
по возрастанию;
- Расставим метки таким образом :
Эвристика
Суть данной эвристики состоит в ранжировании псевдодисперсий и в анализе полученной гистограммы. Под псевдодисперсией будем понимать величины
, где
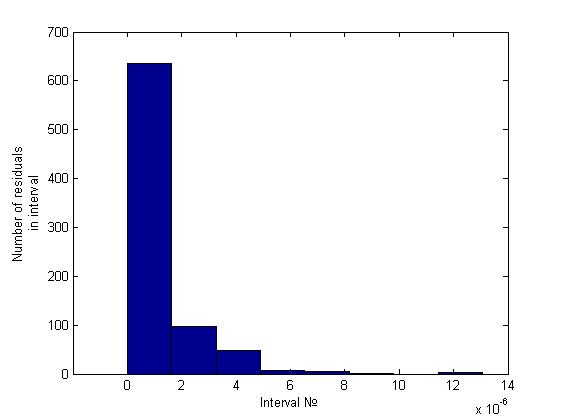
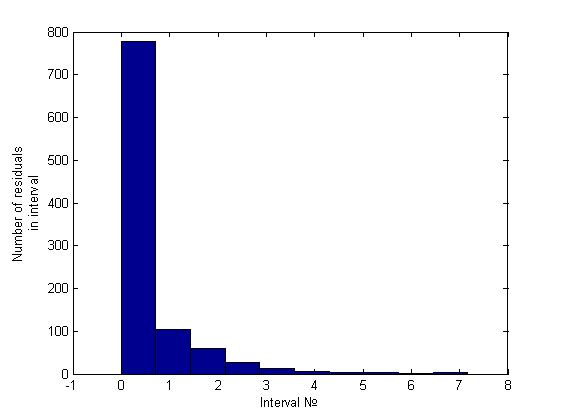
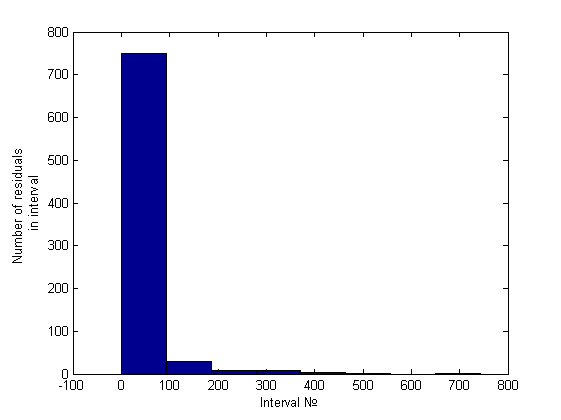
. Простейший анализ гистограммы, состоящей из 10 интервалов, будем проводить сравнением количества элементов на первых двух интервалах. Это отношение будем сравнивать с некоторой, заранее заданной константой, на основе чего и будем принимать решение о гетероскедастичности. Вот пример гистограммы для гомоскедастичного случая (график его остатков был представлен ранее):
Легко заметить, что порядок отношения первых двух столбцов - около пяти-шести к одному, что же касается гетероскедастичного случая, это отношение будет больше семи (было замечено вплоть до 34) примеры можно посмотреть ниже, в вычислительном эксперименте.
Вычислительный эксперимент на модельных данных
В данном отчете представлены результаты применения созданного инструмента анализа представленной модели с помощью исследования ее регрессионных остатков. Отчет состоит из трех экспериментов, демонстрирующих плюсы и минусы созданного инструмента.
Три модели
Представленные модели были подобраны так, чтобы визуальный анализ регрессионных остатков не давал очевидных результатов. Будем проводить исследование в два этапа - вначале проверяя модель на выполнение основных гипотез, затем исследуя модель на гетероскедастичность с помощью теста Голдфелда-Кванта и несложной эвристики.
Модель №1 (хорошая)
Наша модель : , где
. Таким образом все гипотезы должны выполняться и гетероскедастичность должна отсутствовать.
[A,x,res] = GetGoodExample [meanst, distab, normchi2, normjb] = ResAnalysis(res) GoldfeldQuandt(A(:,1:end-1),A(:,end),1) GoldfeldQuandt(A(:,1:end-1),A(:,end),2) HistAnalys(res)
Получаем результат:
% Проверка основных гипотез meanst = 0 distab = 0.0500 normchi2 = 0 normjb = 0 %Проверка на гетероскедастичность% goldfeldquandt1 = 0 goldfeldquandt2 = 0 result = 0
График остатков этой модели уже был приведен выше и не представляет особого интереса.
Модель №2 (плохая, одномерная)
Наша модель : , где
. Таким образом, модель очевидным образом гетероскедастична, но визуальным анализом это сложно обнаружить(см.рисунок).
[A,x,res] = GetBadExample [meanst, distab, normchi2, normjb] = ResAnalysis(res) GoldfeldQuandt(A(:,1:end-1),A(:,end),1) HistAnalys(res)
Получаем результат:
% Проверка основных гипотез meanst = 0 distab = 0.0340 normchi2 = 1.0020 normjb = 1.0020 %Проверка на гетероскедастичность% goldfeldquandt1 = 0 result = 1
Нормальность отвергнута. Гетероскедастичность была обнаружена только эвристикой. Приведем гистограмму полученную эвристикой:
Модель №3 (плохая,многомерная)
Наша модель : , где
. Таким образом, модель очевидным образом гетероскедастична, но снова визуальным анализом это сложно обнаружить(см.рисунок).
[A,x,res] = GetBadExample1 [meanst, distab, normchi2, normjb] = ResAnalysis(res) GoldfeldQuandt(A(:,1:end-1),A(:,end),1) GoldfeldQuandt(A(:,1:end-1),A(:,end),2) GoldfeldQuandt(A(:,1:end-1),A(:,end),5) HistAnalys(res)
Получаем результат:
% Проверка основных гипотез meanst = 0 distab = 0.0288 normchi2 = 1.0025 normjb = 1.0025 %Проверка на гетероскедастичность% goldfeldquandt1 = 1 goldfeldquandt2 = 1 goldfeldquandt5 = 0 result = 1
Нормальность отвергнута. Гетероскедастичность была обнаружена как эвристикой, так и тестом Голдфелда-Квандта (зависимость от первой и второй и независимость от пятой переменной). Приведем гистограмму полученную эвристикой:
Выводы
Статистические проверки на нормальность показали себя с наилучшей стороны. Эвристика показала хорошие результаты в исследовании на гетероскедастичность. Тест Голдфелда-Квандта не сработал только в одном тесте. Тест Ансари-Брэдли (использовался для проверки на постоянство дисперсии) показал наихудшие результаты, так как с его помощью не удалось различить две существенно разные модели. Это вполне объяснимо: мы применяли этот тест для сравнения дисперсий двух случайных выборок взятых из нашего вектора остатков. Вполне очевидно что результат достаточно не предсказуем вследствие именно этой случайности выборок. В итоге мы получали одинаковые результаты для разных моделей. (причем увеличение числа экспериментов не решает данной проблемы).
Исходный код
Функции анализирующие остатки (реализовано в MATLAB)
См. также
Wikipedia о гетероскедастичности, англ.
Литература
- Н.Джонсон, Ф.Лион Статистика и планирование эксперимента в технике и науке, перевод с английского «Мир»,1980. — 610 c.
- Я. Р. Магнус, П. К. Катышев, А. А. Пересецкий Эконометрика. Начальный курс:Учеб. — 6 изд.,перераб.и доп. — М.:Дело,2004. — 576 с. ISBN 5-7749-0055-Х
- Applied Logistic Regression/ David W. Hosmer,Stanley Lemeshow.-2nd ed. -Wiley-Interscience Publication,2000. - 397 c. ISBN 0-471-35632-8
- Кобзарь А. И. Прикладная математическая статистика. — М.: Физматлит, 2006. — 816 с. ISBN 5-9221-0707-0
| | Данная статья была создана в рамках учебного задания.
См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе. |