Статистический анализ данных (курс лекций, К.В.Воронцов)/2010
Материал из MachineLearning.
Содержание |
Задание 1. Исследование свойств одномерных статистических критериев на модельных данных
Необходимо провести исследование одного или нескольких классических критериев проверки статистических гипотез. Интерес представляет поведение достигаемого уровня значимости (p-value) как функции размера выборок и параметров распределения. В соответствии с индивидуальными параметрами задания необходимо указанным способом сгенерировать одну или несколько выборок из заданного распределения, выполнить проверку гипотезы при помощи соответствующего критерия, а затем многократно повторить эту процедуру для различных значений параметров. По результатам расчётов необходимо построить требуемые в задании графики, среди которых могут быть следующие:
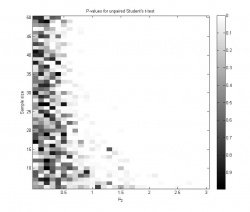
- график зависимости достигаемого уровня значимости от значений параметров при однократном проведении эксперимента;
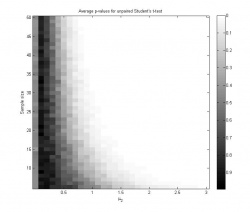
- график зависимости достигаемого уровня значимости от значений параметров, усреднённого по большому количеству повторений эксперимента (например, по 100, 500, 1000 повторений);
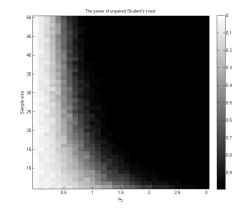
- график с эмпирическими оценками мощности критерия для разных значений параметров.
В качестве оценки мощности принимается доля отвержений нулевой гипотезы среди всех проверок. То есть, если эксперимент повторялся раз для каждого набора значений параметра, и в
из
случаев гипотеза была отвергнута на некотором фиксированном уровне значимости
(примем
), оценкой мощности будет отношение
.
Необходимо сдать: выполненный в LaTex или Microsoft Word отчёт с описанием алгоритма, построенными графиками и выводами (объяснение полученных результатов моделирования, границы применимости критерия и т.д.), а также *.m-файл, при запуске которого на экран выводятся графики, соответствующие имеющимся в отчёте (допускается, хотя и не рекомендуется использование среды R).
Пример задания
Исследуем поведение классического двухвыборочного критерия Стьюдента для проверки гипотезы однородности против альтернативы сдвига при разных значениях параметров.
При каждом значении выборки для разных значений
генерируются независимо.
Задания
Анализ устойчивости критериев к нарушению предположений
- Исследовать устойчивость одновыборочного критерия Стьюдента к нарушению предположения о нормальности данных.
— смесь распределений
и
с весами
и
соответственно (при генерации выборки используется случайный датчик — если его значение не превосходит
, то добавляем в выборку элемент, взятый из нормального распределения, иначе — элемент, взятый из равномерного). Для разных значений параметров выборки генерируются независимо.
Построить графики вида 1, 2, 3, сделать выводы о чувствительности критерия к зашумлению выборки.
- Вишневский Валерий:
- Гарсиа Анхела:
- Дергунов Вадим:
- Вишневский Валерий:
- Исследовать устойчивость двухвыборочного критерия Стьюдента для независимых выборок к нарушению предположения о нормальности данных.
— смесь распределений
и
с весами
и
соответственно (при генерации выборки используется случайный датчик — если его значение не превосходит
, то добавляем в выборку элемент, взятый из нормального распределения, иначе — элемент, взятый из равномерного). Для разных значений параметров выборки генерируются независимо.
Построить графики вида 1, 2, 3, сделать выводы о чувствительности критерия к зашумлению одной из выборок.
- Добров Григорий:
- Дячкин Олег:
- Ерошенко Александр:
- Добров Григорий:
Анализ чувствительности критериев к редактированию выборки
- Известно, что исключение из выборки определённых наблюдений зачастую может достаточно сильно повлиять на результат анализа. Необходимо исследовать чувствительность одновыборочного критерия критерия Стьюдента к редактированию выборки.
При каждом значении параметрагенерируется выборка размера
, проводится проверка гипотезы
, затем по некоторому правилу из выборки исключается один из элементов, проверка гипотезы повторяется, затем исключается ещё один, и т.д. Обозначим за
максимальное число исключённых в таком процессе элементов. Построить графики вида 1, 2, 3, сделать выводы о чувствительности критерия к редактированию выборки.
- Когадеева Мария:
на каждом шаге исключается максимальный элемент.
- Колесниченко Алексей:
на каждом шаге исключается максимальный элемент.
- Кошманова Наталья:
на каждом шаге исключается минимальный элемент.
- Лаптев Дмитрий:
на каждом шаге исключается минимальный элемент.
- Когадеева Мария:
Анализ поведения схожих критериев
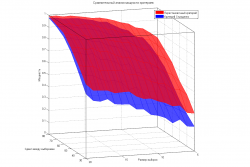
Требуется исследовать поведение указанной пары статистических критериев, подходящих для решения одной и той же задачи, сравнить мощность и достигаемые уровни значимости и сделать выводы о границах применимости критериев. Необходимо для каждого из критериев построить графики зависимости достигаемых уровней значимости и оценок мощностей от параметров, и показать, в каких областях изменения параметров предпочтительнее использовать тот или иной критерий. Выбрать вид графиков так, чтобы различия между критериями были видны наиболее ясно (например, график вида 4).
- Логачев Юрий: двухвыборочный критерий Стьюдента для независимых выборок и критерий Уилкоксона-Манна-Уитни.
- Полежаева Елена: двухвыборочный критерий Стьюдента для связных выборок и критерий Уилкоксона для связных выборок.
- Прокашева Ольга: двухвыборочные критерий Стьюдента для связных и независимых выборок.
- Пятков Евгений: критерий Уилкоксона-Манна-Уитни и медианный критерий.
- Сизов Алексей: критерий Уилкоксона для связных выборок и критерий знаков.
- Кожахметова Жанна: критерий знаков и медианный критерий.
-
связь между признаками в таблице сопряжённости 2×2, задаваемой величинами
отсутствует;
признаки связаны между собой.
- Слепнева Екатерина: критерий хи-квадрат и точный критерий Фишера.
- Тишин Кирилл: критерий хи-квадрат и точный критерий Фишера.
- Слепнева Екатерина: критерий хи-квадрат и точный критерий Фишера.
-
— смесь распределений
и
с весами
и
соответственно (при генерации выборки используется случайный датчик — если его значение не превосходит
, то добавляем в выборку элемент, взятый из нормального распределения, иначе — элемент, взятый из равномерного).
неверна;
- Чернышов Виктор: критерий Шапиро-Уилка и критерий Колмогорова-Смирнова.
- Чиркова Алла: критерий омега-квадрат и критерий Шапиро-Уилка.
- Шевцова Алена: критерий хи-квадрат и критерий омега-квадрат.
- Щичко Антон: критерий Колмогорова-Смирнова и критерий хи-квадрат.
- Чернышов Виктор: критерий Шапиро-Уилка и критерий Колмогорова-Смирнова.
Задание 2. Анализ реальных данных
Ниже приведены описания анализируемых данных и постановки задач. Сами данные каждый студент может получить по электронной почте сразу после сдачи первого задания. При проведении анализа можно пользоваться любыми доступными программными средствами. Необходимо предоставить подробный письменный отчёт по проведённому исследованию, содержащий выводы и описания каждого этапа анализа — используемые методы, обоснование их применимости, промежуточные результаты вычислений, графики. Помимо выводов, касающихся математических особенностей решения, необходимо включить в отчёт заключения, сформулированные в терминах предметной области, которые могли бы быть понятны гипотетическому заказчику-нематематику.
Летальность пациентов с сепсисом
По 454 пациентам с сепсисом (лихорадка, тахикардия, тахипноэ и острая недостаточность по крайней мере одной системы органов) имеются следующие данные: оценка начального состояния по шкале APACHE острых и хронических функциональных изменений, факт наступления смерти в течение 30 дней после начала исследования (для каждого значения APACHE score приведены общее число пациентов в таком состоянии и соответствующее число пациентов, умерших в течение 30 дней).
- Когадеева Мария: Оценить вероятность наступления в 30-дневный срок летального исхода в зависимости от исходного состояния. Построить функции, дающие точечную оценку и границы 95% доверительного интервала.
Линейные размеры швейцарских банкнот
Имеются данные измерений двухсот швейцарских тысячефранковых банкнот, бывших в обращении в первой половине XX века. Сто из банкнот были настоящими, а сто - поддельными. Измерены следующие величины: — длина банкноты,
—ширина банкноты с левой стороны,
—ширина банкноты с правой стороны,
—расстояние от нижнего края до рамки рисунка,
— расстояние от нижнего края до рамки рисунка,
— длина диагонали рисунка.
- Логачев Юрий: Построить функцию, оценивающую по данным измерений вероятность того, что имеющаяся банкнота фальшивая, и 95% доверительный интервал для этой вероятности.
- Пятков Евгений: Построить функции, оценивающие вероятность того, что имеющаяся банкнота фальшивая, по признакам
и по признакам
. Сравнить эффективность выявления фальшивых купюр по двум группам признаков.