Статистический анализ данных (курс лекций, К.В.Воронцов)/2011, ФУПМ
Материал из MachineLearning.
|
Задание 1. Исследование свойств одномерных статистических критериев на модельных данных
Необходимо провести исследование одного из классических критериев проверки статистических гипотез. Интерес представляет поведение достигаемого уровня значимости (p-value) как функции размера выборок и параметров распределения. В соответствии с индивидуальными параметрами задания необходимо указанным способом сгенерировать одну или несколько выборок из заданного распределения, выполнить проверку гипотезы при помощи соответствующего критерия, а затем многократно повторить эту процедуру для различных значений параметров. По результатам расчётов необходимо построить следующие графики:
- график зависимости достигаемого уровня значимости от значений параметров при однократном проведении эксперимента;
- график зависимости достигаемого уровня значимости от значений параметров, усреднённого по большому количеству повторений эксперимента (например, по 100, 500, 1000 повторений — чем больше, тем лучше);
- график с эмпирическими оценками мощности критерия для разных значений параметров.
В качестве оценки мощности принимается доля отвержений нулевой гипотезы среди всех проверок. То есть, если эксперимент повторялся раз для каждого набора значений параметра, и в
из
случаев гипотеза была отвергнута на некотором фиксированном уровне значимости
(примем
), оценкой мощности будет отношение
.
Необходимо сдать: отчёт с описанием алгоритма, построенными графиками и выводами (объяснение полученных результатов моделирования, границы применимости критерия и т.д.), а также файл с текстом программы на использованном языке (Matlab, R, и т.д.), при выполнении которой проводятся указанные в задаче вычисления и на экран выводятся графики, соответствующие имеющимся в отчёте.
Задание принимается до девятого апреля.
Пример задания
Исследуем поведение классического двухвыборочного критерия Стьюдента для проверки гипотезы однородности против альтернативы сдвига при разных значениях параметров.
При каждом значении выборки для разных значений
генерируются независимо.
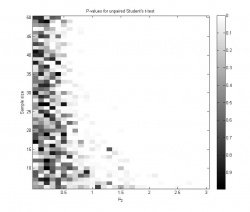
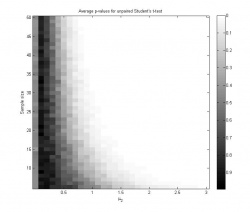
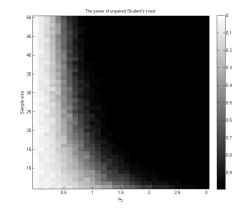
Графики 1 и 2 иллюстрируют зависимость достигаемого уровня значимости от размера выборки и среднего . На графике 3 показана зависимость мощности критерия от параметров задачи; мощность в каждой точке оценивается как доля экспериментов, в которых гипотеза была отвергнута на уровне значимости
.
- Видно, что при
среднее значение достигаемого уровня значимости при многократном повторении эксперимента равно 0.5 для любого размера выборки. Это логично, так как при
нулевая гипотеза справедлива, и достигаемый уровень значимости имеет равномерное распределение на
- При
и
критерий имеет достаточную мощность, и нулевая гипотеза чаще всего отвергается.
- При размере выборки до 50 элементов и среднем второй выборки
критерий практически не способен отклонить гипотезу однородности, мощность в этой области изменения параметров низка.
- При большой разнице между средними выборок
критерий достаточно уверенно отвергает гипотезу однородности даже на выборках небольшого размера (5-6 элементов).
Задания
Устойчивость критериев к нарушению предположений
Исследовать поведение параметрических критериев, предполагающих нормальность данных, при зашумлении выборок наблюдениями, взятыми из равномерного распределения. Построить графики вида 1, 2, 3, сделать выводы о чувствительности критерия к зашумлению.
- Двухвыборочный критерий Стьюдента для независимых выборок.
— выборка длины
из смеси нормального
и равномерного
распределений с весами
и
соответственно (при генерации выборки используется случайный датчик — если его значение не превосходит
, то добавляем в выборку элемент, взятый из нормального распределения, иначе — элемент, взятый из равномерного).
— аналогичная выборка.
- Кононенко Даниил:
- Голкин Александр:
- Завадский Глеб:
- Чугунов Кирилл:
- Корниенко Алексей:
- Кузнецов Михаил:
- Кононенко Даниил:
- Критерий Фишера для проверки равенства дисперсий.
— выборка длины
из смеси нормального
и равномерного
распределений с весами
и
соответственно (при генерации выборки используется случайный датчик — если его значение не превосходит
, то добавляем в выборку элемент, взятый из нормального распределения, иначе — элемент, взятый из равномерного).
— аналогичная выборка.
- Иванов Николай:
- Рубцов Александр:
- Рукина Дарья:
- Савгиров Арш:
- Спиридонов Роман:
- Стукалюк Владимир:
- Иванов Николай:
Влияние связок на поведение статистических критериев
Многие статистические критерии неявно предполагают, что выборка извлечена из абсолютно непрерывного распределения, что значит, что вероятность наличия в ней одинаковых элементов равна нулю. Необходимо исследовать поведение такого критерия в случае наличия в выборке совпадающих значений. Построить графики вида 1, 2, 3, сделать выводы о чувствительности критерия к наличию связок.
Для генерации выборки со связками может использоваться округление элементов выборки, либо следующая процедура:
- генерируется выборка
размера
из указанного в задаче распределения;
- в вариационном ряду выборки
выбираются
непересекающихся пар элементов
, лежащих ближе всего друг к другу;
- для всех
выбранных пар элементы выборки
и
заменяются их средним.
- Статистические критерии, проверяющие гипотезу нормальности.
— выборка длины
из смеси нормального
и равномерного
распределений с весами
и
соответственно (при генерации выборки используется случайный датчик — если его значение не превосходит
, то добавляем в выборку элемент, взятый из нормального распределения, иначе — элемент, взятый из равномерного);
распределена нормально;
распределена по какому-то другому закону.
- Сунгуров Дмитрий: критерий Андерсона-Дарлинга, указанная процедура порождения связок,
- Животовский Никита: критерий Шапиро-Уилка, указанная процедура порождения связок,
- Мафусалов Александр: критерий Андерсона-Дарлинга, округление элементов выборки до десятых,
- Сечин Павел: критерий Шапиро-Уилка, округление элементов выборки до десятых,
- Сунгуров Дмитрий: критерий Андерсона-Дарлинга, указанная процедура порождения связок,
- Джамтырова Раиса: элементы выборок округляются до десятых,
- Ивкин Никита: элементы выборок округляются до 0.5,
- Пронин Яков: указанная процедура порождения связок,
- Фирстенко Александр: указанная процедура порождения связок,
- Джамтырова Раиса: элементы выборок округляются до десятых,
Анализ чувствительности критериев к редактированию выборки
Известно, что исключение из выборки определённых наблюдений зачастую может достаточно сильно повлиять на результат анализа. Необходимо исследовать чувствительность указанного критерия к редактированию выборки, построить графики вида 1, 2, 3, сделать выводы.
- Одновыборочный критерий Стьюдента.
При каждом значении параметра генерируется выборка размера
, проводится проверка гипотезы
, затем по некоторому правилу из выборки исключается один из элементов, проверка гипотезы повторяется, затем исключается ещё один, и т.д. Обозначим за
максимальное число исключённых в таком процессе элементов.
- Фадеев Илья:
на каждом шаге исключается максимальный элемент.
- Берновский Михаил:
на каждом шаге исключается максимальный элемент.
- Бессарабов Никита:
на каждом шаге исключается минимальный элемент.
- Гнедков Игорь:
на каждом шаге исключается минимальный элемент.
- Фадеев Илья:
- Двухвыборочный критерий Стьюдента.
На каждом шаге генерируются выборки исходной длины, проводится проверка гипотезы , затем по некоторому правилу из указанной выборки исключается один из элементов, проверка гипотезы повторяется, затем исключается ещё один, и т.д. Обозначим за
максимальное число исключённых в таком процессе элементов.
- Фирстенко Александр:
на каждом шаге исключается максимальный элемент
.
- Татарников Дмитрий:
на каждом шаге исключается минимальный элемент
.
- Зайцев Евгений:
на каждом шаге исключается максимальный элемент
.
- Морозов Алексей:
на каждом шаге исключается минимальный элемент
.
- Фирстенко Александр:
Литература
Кобзарь А. И. Прикладная математическая статистика. — М.: Физматлит, 2006.