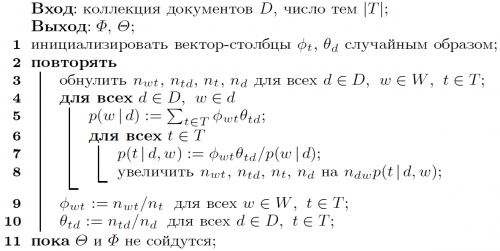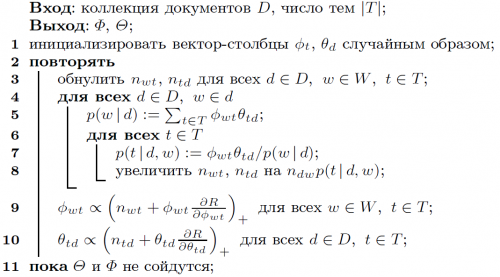Аддитивная регуляризация тематических моделей
Материал из MachineLearning.
|
Аддитивная регуляризация тематических моделей — многокритериальный подход к построению вероятностных тематических моделей коллекций текстовых документов. Охватывает наиболее известные тематические модели PLSA, LDA и многие байесовские модели. Является альтернативой байесовскому обучению тематических моделей.
Основные отличия от байесовского подхода:
- простой математический аппарат;
- регуляризаторы не обязаны иметь вероятностную интерпретацию;
- легко комбинировать регуляризаторы из разных моделей и строить многофункциональные тематические модели;
- легко реализовать огромное разнообразие тематических моделей в одной библиотеке, см. BigARTM.
Теория
Тематическое моделирование
Вероятностное тематическое моделирование — это современный инструмент статистического анализа текстов, предназначенный для выявления тематики коллекций документов. Тематическая модель описывает каждую тему дискретным распределением на множестве терминов, каждый документ — дискретным распределением на множестве тем. Тематические модели используются для информационного поиска, классификации, категоризации, аннотирования, сегментации текстов.
Тематическая модель — это представление наблюдаемого условного распределения терминов (слов или словосочетаний)
в документах
коллекции
:
где — множество тем;
— неизвестное распределение терминов в теме
;
— неизвестное распределение тем в документе
.
Параметры тематической модели — матрицы и
находятся путём решения задачи максимизации правдоподобия
при ограничениях нормировки и неотрицательности
где — число вхождений слова
в документ
.
Данная задача некорректно поставлена и имеет в общем случае бесконечно много решений вида
.
Отсюда вытекают проблемы неустойчивости и плохой интерпретируемости тематических моделей.
В вероятностном латентном семантическом анализе (PLSA) для решения данной задачи используется EM-алгоритм. На каждой итерации ЕМ-алгоритма выполняется два шага:
- E-шаг:
- M-шаг:
- E-шаг:
EM-алгоритм для PLSA сходится к одному из локальных решений.
Аддитивная регуляризация тематических моделей
Для решения проблемы неединственности и неустойчивости используется регуляризация. На искомое решение накладываются дополнительные ограничения.
Подход АРТМ основан на идее многокритериальной регуляризации. Он позволяет строить модели, удовлетворяющие многим ограничениям одновременно. Каждое ограничение формализуется в виде регуляризатора — оптимизационного критерия , зависящего от параметров модели. Взвешенная сума всех таких критериев
максимизируется совместно с основным критерием правдоподобия.
при тех же ограничениях нормировки и неотрицательности.
Для решения задачи регуляризованного правдоподобия используется EM-алгоритм с модифицированными формулами M-шага:
Для комбинирования регуляризаторов в АРТМ необходимо продумывать стратегию регуляризации:
- какие регуляризаторы необходимы в данной задаче;
- какие регуляризаторы должны работать одновременно, какие друг за другом или попеременно, делая необходимую подготовительную работу;
- как менять коэффициент регуляризации каждого регуляризатора в ходе итераций: по каким условиям включать, усиливать, ослаблять и отключать каждый регуляризатор.
Ограничения подхода АРТМ:
- Коэффициенты регуляризации приходится подбирать вручную. Автоматическая коррекция стратегий регуляризации в АРТМ пока является открытой проблемой.
Регуляризаторы
Следующие регуляризаторы реализованы в библиотеке BigARTM.
- Сглаживание распределений терминов в темах. Используется для выделения фоновых тем, собирающих общую лексику языка или общую лексику данной коллекции.
- Сглаживание распределений тем в документах. Используется для выделения фоновых слов в каждом документах.
- Разреживание распределений терминов в темах. Используется для выделения лексических ядер предметных тем как относительно небольшой доли слов словаря.
- Разреживание распределений тем в документах. Используется для выделения относительно небольшой доли предметных тем в каждом документах.
- Декоррелирование распределений терминов в темах. Используется для повышения различности лексических ядер предметных тем.
- Отбор тем путём обнуления вероятности темы во всех документах. Используется для выведения из модели незначимых тем. Позволяет оптимизировать число тем, начиная с заведомо избыточного числа тем и постепенно удаляя ненужные.
Модели PLSA и LDA
Две самые известные тематические модели — PLSA и LDA — реализуются как частные случаи в АРТМ:
- PLSA (Probabilistic Latent Semantic Analysis) — это тематическая модель без регуляризаторов.
- LDA (Latent Dirichlet Allocation) — это тематическая модель, в которой каждая тема сглажена одним и тем же регуляризатором Дирихле.
В АРТМ рекомендуется использовать небольшое число сглаженных тем (можно одну), чтобы моделировать общую лексику языка, а к остальным темам применять регуляризаторы разреживания и декоррелирования, чтобы помочь тематической модели выделить в них специфические темы предметных областей данной текстовой коллекции.
Параллельный онлайновый EM-алгоритм
Онлайновый EM-алгоритм реализует наиболее эффективную схему вычислений, при которой большие коллекции документов обрабатываются вообще за одну итерацию. Это возможно благодаря тому, что в матричном разложении матрица
зависит от всей коллекции, тогда как в матрице
каждый столбец зависит от своего документа. На больших коллекциях темы неплохо определяются по небольшой доле документов. Поэтому матрица
успевает сойтись задолго до того, как заканчивается первая итерация.
В онлайновом EM-алгоритме коллекция разделяется на пакеты документов. Каждый пакет обрабатывается при фиксированной матрице
, при этом для каждого документа из пакета производится несколько итераций до сходимости. На каждой итерации вычисляются переменные
. Переменные
обновляются гораздо реже, после обработки каждого пакета.
Онлайновый алгоритм не держит в памяти всю коллекцию. Пакеты документов загружаются и выгружаются по необходимости. Это позволяет обрабатывать сколь угодно большие коллекции, которые не помещаются целиком ни в оперативную память, ни даже на диск одного компьютера. Эксперименты показывают, что качество модели и время обработки слабо зависят от размера пакетов, причём с ростом размера коллекции эта зависимость становится ещё менее заметной.
В ARTM онлайновый EM-алгоритм обобщён для мультимодальных регуляризованных моделей.
Параллельная архитектура BigARTM разработана исходя из требований асинхронной обработки данных, минимизации используемого объёма оперативной памяти, масштабируемости при увеличении количества ядер на узле, кроссплатформенности, возможности быстрой установки и использования на одной машине.
Для организации параллельной обработки данных на одном узле используется многопоточный параллелизм в пределах одного процесса. Это позволяет получить хорошую скорость обработки и хранить общую матрицу для узла, а не для каждого ядра. Кроме того, обеспечивается возможность асинхронной работы с данными.
Мультимодальные тематические модели
Мультимодальные тематические модели учитывают метаданные документа — информацию, дополнительную по отношению к основному тексту. Метаданные могут помогать выявлять тематику документа, и, наоборот, определив тематику документа по его тексту, можно автоматически формировать метаданные, восполнять пропущенные метаданные, строить рекомендации для пользователей.
В тематических моделях могут учитываться метаданные различных типов: авторы, метки времени создания документа или его фрагментов, категории, изображения и отдельные элементы изображений, цитируемые документы, цитируемые авторы, пользователи документов и т.д.
BigARTM реализует мультимодальные модели, позволяющие обрабатывать метаданные любого числа типов одновременно. Для каждой модальности создаётся словарь возможных значений. Вхождение элементов каждой модальности рассматривается точно так же, как вхождение терминов в текст. По сути дела, термины (слова и словосочетания) — это лишь элементы одной из модальностей. Мультимодальная тематическая модель строит для каждой темы дискретное вероятностное распределение на конечном множестве (словаре) всех элементов каждой модальности.
Сравнение с байесовскими моделями
Вероятностное тематическое моделирование развивается, главным образом, в рамках байесовского обучения и графических моделей. В байесовском подходе коллекция текстов описывается единой вероятностной порождающей моделью, при этом учёт дополнительных данных и формализация дополнительных ограничений производится через априорные распределения.
Недостатки байесовского подхода в тематическом моделировании:
- Многие требования к модели удобно вводить через оптимизационные критерии. Их переформулировка в терминах априорных распределений сильно усложняет байесовский вывод. Комбинирование нескольких априорных распределений не может быть сделано эффективно в общем виде.
- Байесовское обучение определяет не сами параметры модели, а их распределения. Однако в тематическом моделировании найденные распределения используются исключительно для оценивания математических ожиданий. Таким образом, решается намного более трудная задача, чем это необходимо.
- Многие байесовские модели вынужденно используют априорное распределение Дирихле. Оно математически удобно благодаря сопряжённости с мультиномиальным распределением. Однако оно не моделирует каких-либо явлений естественного языка и не имеет убедительных лингвистических обоснований. Более того, оно противоречит естественному требованию разреженности, не допуская нулевых значений в матрицах
и
.
- Априорное распределение Дирихле является слишком слабым регуляризатором. Проблему неединственности и неустойчивости модели он не решает.
Преимущества подхода АРТМ:
- В АРТМ регуляризаторы не обязаны быть априорными распределениями и иметь какую-либо вероятностную интерпретацию.
- Регуляризатор Дирихле утрачивает свою особую роль, его не обязательно использовать в каждой модели для всех тем.
- Математический аппарат очень прост: чтобы добавить регуляризатор, достаточно добавить его производные в формулы М-шага.
- Многие байесовские тематические модели (или заложенные в них идеи) удаётся переформулировать через регуляризаторы.
- Суммируя регуляризаторы, взятые из разных моделей, можно строить многоцелевые комбинированные модели.
- Тематические модели в АРТМ легче понимать, легче выводить и легче комбинировать.
- Снижается порог вхождения в область тематического моделирования для исследователей из смежных областей.
Литература
- Воронцов К.В. Вероятностное тематическое моделирование: теория регуляризации ARTM и библиотека с открытым кодом BigARTM. 2024.
- Воронцов К. В. Аддитивная регуляризация тематических моделей коллекций текстовых документов // Доклады РАН. 2014. — Т. 455., №3. 268–271
- Воронцов К. В. Потапенко А. А. Регуляризация вероятностных тематических моделей для повышения интерпретируемости и определения числа тем // Компьютерная лингвистика и интеллектуальные технологии: По материалам ежегодной Международной конференции «Диалог» (Бекасово, 4–8 июня 2014 г.) Вып.13 (20). М: Изд-во РГГУ, 2014. C.676–687.
- Vorontsov K. V. Additive Regularization for Topic Models of Text Collections // Doklady Mathematics. 2014, Pleiades Publishing, Ltd. — Vol. 89, No. 3, pp. 301–304.
- Vorontsov K. V., Potapenko A. A. Tutorial on Probabilistic Topic Modeling: Additive Regularization for Stochastic Matrix Factorization // AIST’2014, Analysis of Images, Social networks and Texts. Springer International Publishing Switzerland, 2014. Communications in Computer and Information Science (CCIS). Vol. 436. pp. 29–46.
- Vorontsov K. V., Potapenko A. A. Additive Regularization of Topic Models // Machine Learning Journal. Special Issue “Data Analysis and Intelligent Optimization with Applications”. Русский перевод
См. также
- Тематический анализ больших данных. Краткое популярное введение в ARTM и BigARTM.
- Тематическое моделирование.
- BigARTM, bigartm.org — библиотека с открытым кодом для тематического моделирования больших коллекций.
- Коллекции документов для тематического моделирования.
- Вероятностные тематические модели — семестровый спецкурс, кафедра ММП ВМиК МГУ.