Математические методы классификации (курс лекций, К.В. Рудаков)
Материал из MachineLearning.
(→Содержание курса) |
(+ часть 2) |
||
| (1 промежуточная версия не показана) | |||
| Строка 8: | Строка 8: | ||
== Аннотация == | == Аннотация == | ||
| - | Основу данного курса составляют теория категорий и теория универсальных и локальных ограничений для задач классификации и распознавания. В курс входит построение теории категорий, изучение понятий категорий, подкатегорий, | + | Основу данного курса составляют теория категорий и теория универсальных и локальных ограничений для задач классификации и распознавания. В курс входит построение теории категорий, изучение понятий категорий, подкатегорий, морфизфов (мономорфизм, эпиморфизм, биморфизм). Рассмотрена задача синтеза алгоритмов, изучены понятия допустимых и корректных алгоритмов, понятие разрешимости. Так же введены понятия полноты семейства алгоритмов и категорий, базы категорий. Изучен критерий регулярности задач классификации. Рассмотрены понятия функциональной сигнатуры и универсальных ограничений. |
== Содержание курса == | == Содержание курса == | ||
| Строка 15: | Строка 15: | ||
=== Морфизмы === | === Морфизмы === | ||
| - | Мономорфизмы. Теорема о композиции мономорфизмов. | + | Мономорфизмы. Теорема о композиции мономорфизмов. Мономорфизмы в категории отображений. Эпиморфизмы. Теорема о композиции эпиморфизмов. Эпиморфизмы в категории отображений. Изоморфизмы и биморфизмы. Пример неэквивалентности. |
=== Элементы теории множеств === | === Элементы теории множеств === | ||
| - | Декартово произведение произвольной | + | Декартово произведение произвольной индексированной системы множеств. Аксиома выбора. Парадокс Рассела. Отношение эквивалентности множеств и теорема Кантора-Бернштейна. Парадокс Кантора. Разложение произвольного отображения в суперпозицию отображений определенного вида. Булевы функции. Неявные булевы функции. |
=== Алгебраический подход === | === Алгебраический подход === | ||
| - | Общий вид алгоритмов, синтезируемых методами | + | Общий вид алгоритмов, синтезируемых методами алгебраического подхода. Лемма о достаточности условий допустимости. Регулярность задач распознавания. Обоснование необходимости условия полноты. Определения баз категорий. Лемма об эквивалентности определений баз для полных допустимых категорий. |
=== Базы === | === Базы === | ||
| - | Общая схема перехода от пространства матриц информации к | + | Общая схема перехода от пространства матриц информации к пространству информационных матриц. Лемма о необходимости для, вообще говоря, неодноэлементных баз. Лемма о достаточности для одноэлементных баз. |
=== Г-Полнота === | === Г-Полнота === | ||
| - | Общий критерий регулярности. Условие 1-Г-полноты. Условие | + | Общий критерий регулярности. Условие 1-Г-полноты. Условие слабой 1-Г-пол-ноты. Корректность. Условие Г-полноты. Условие слабой Г-полноты. Теорема о полноте алгебраических расширений. |
=== Симметрические универсальные ограничения === | === Симметрические универсальные ограничения === | ||
| - | Определение. Лемма о | + | Определение. Лемма о достаточности использования подгрупп. Лемма о допустимости симметрических категорий. Лемма о полноте симметрических категорий. Лемма о базах. |
=== Функциональные сигнатуры и универсальные ограничения === | === Функциональные сигнатуры и универсальные ограничения === | ||
| Строка 39: | Строка 39: | ||
== Литература == | == Литература == | ||
| + | # {{П:Рудаков 1992 Алгебраическая теория}} | ||
# Букур И., Деляну А. Ведение в теорию категорий и функторов. М.: Мир. 1972. | # Букур И., Деляну А. Ведение в теорию категорий и функторов. М.: Мир. 1972. | ||
# Журавлев Ю.И. Избранные научные труды. М.: Магистр. 1999. | # Журавлев Ю.И. Избранные научные труды. М.: Магистр. 1999. | ||
| Строка 45: | Строка 46: | ||
# Ленг С. Алгебра. М.: Мир. 1968. | # Ленг С. Алгебра. М.: Мир. 1968. | ||
# Мальцев А.И. Алгебраические системы. М.: Наука. 1970. | # Мальцев А.И. Алгебраические системы. М.: Наука. 1970. | ||
| - | # Матросов В.Л. Корректные алгебры ограниченной емкости над множествами | + | # Матросов В.Л. Корректные алгебры ограниченной емкости над множествами некорректных алгоритмов // ДАН СССР. 1980. Т. 253. № 1. С. 25-30. |
| - | # Рудаков К.В. Универсальные и локальные ограничения в проблеме коррекции | + | # Рудаков К.В. Универсальные и локальные ограничения в проблеме коррекции эвристических алгоритмов классификации // Кибернетика. 1987. № 2. С. 30-34. |
| - | # Рудаков К.В. Полнота и универсальные ограничения в проблеме коррекции | + | # Рудаков К.В. Полнота и универсальные ограничения в проблеме коррекции эвристических алгоритмов классификации // Кибернетика. 1987. № 3. С. 106-109. |
| - | # Рудаков К.В. Симметрические и функциональные ограничения в проблеме | + | # Рудаков К.В. Симметрические и функциональные ограничения в проблеме коррекции эвристических алгоритмов классификации // Кибернетика. 1987. № 4. С. 35-40. |
# Рудаков К.В. О применимости универсальных ограничений при исследовании алгоритмов классификации // Кибернетика. 1987. № 5. С. 32-38. | # Рудаков К.В. О применимости универсальных ограничений при исследовании алгоритмов классификации // Кибернетика. 1987. № 5. С. 32-38. | ||
| - | # Рудаков К.В. Об алгебраической теории универсальных и локальных | + | # Рудаков К.В. Об алгебраической теории универсальных и локальных ограничений для задач классификации // Распознавание, классификация, прогноз. Математические методы и их применение. Вып. 1. М.: Наука. 1989. С. 176-200. |
# Фейс С. Алгебра: кольца, модули и категории: В 2-х т. М.: Мир. 1979. | # Фейс С. Алгебра: кольца, модули и категории: В 2-х т. М.: Мир. 1979. | ||
| Строка 61: | Строка 62: | ||
== Аннотация == | == Аннотация == | ||
| - | Данный курс составляет часть алгебраического подхода к проблеме синтеза | + | Данный курс составляет часть алгебраического подхода к проблеме синтеза алгоритмов распознавания. В курс входит построение теории категорий, изучение свойств функциональных и симметрических категорий, баз и полноты категорий, соотношений категорий (функциональные подкатегории симметрических категорий и симметрические подкатегории функциональных категорий). Так же в данном курсе изложены основные принципы построения R и Г моделей, классы решаемых задач, их регулярность, полнота и семейства подмоделей. Рассмотрены семейства корректирующих операций, изучены понятия полноты и суперполноты моделей. |
== Содержание курса == | == Содержание курса == | ||
| Строка 71: | Строка 72: | ||
=== Одноэлементная база категории <tex>\Phi_0</tex> === | === Одноэлементная база категории <tex>\Phi_0</tex> === | ||
| - | Лемма о существовании одноэлементной базы категории | + | Лемма о существовании одноэлементной базы категории <tex>\Phi_0</tex> в линейной оболочке базы. |
| - | + | ||
| - | + | === Полнота семейств === | |
| - | + | Теорема о полноте семейства <tex>A^{ql-1}</tex>. Теорема о полноте семейства <tex>LM^{](ql-1)/2[}</tex>. Теорема о 0-1 полноте модели <tex>M(\gamma_m,\varepsilon)</tex>. Теорема о 0-1 полноте семейства <tex>A^{[\log_2ql]}</tex>. Теорема о 0-1 полноте семейства <tex>LM^1</tex>. | |
| - | + | ||
| - | + | === Категории <tex>\Phi_0</tex> и <tex>\Sigma_0</tex> === | |
| - | + | Критерий разрешимости для категорий <tex>\Phi_0</tex> и <tex>\Sigma_0</tex>. Теорема о суперполноте для категории <tex>\Phi_0</tex>. Теорема о суперполноте для категории <tex>\Sigma_0</tex>. | |
| + | |||
| + | === Замыкания модели <tex>M(R_j,\gamma_m,x)</tex> === | ||
| + | Прямая теорема о полноте линейного замыкания модели <tex>M(R_j,\gamma_m,x)</tex>. Прямая теорема о полноте полиномиального замыкания модели <tex>M(R_j,\gamma_m,x)</tex>. | ||
| + | |||
| + | === Глобальный и локальный базисы для задач распознавания === | ||
| + | Общий итерационный процесс построения локальных базисов задач распознавания. Построение локального базиса в комитете большинства. Построение локального базиса в комитете старшинства. Построение локального базиса в алгоритме бустинга AdaBoost. | ||
| + | |||
| + | === Монотонные корректирующие операции === | ||
| + | Дефект алгоритмического оператора. Дефект набора алгоритмических операторов. Построение локального базиса для случая монотонных корректирующих операций. Теорема о сходимости итерационного процесса построения проблемно-ориентированного базиса за конечное число шагов в случае монотонных корректирующих операций. | ||
| + | |||
| + | === Проблемно-ориентированные теории === | ||
| + | Задачи синтеза алгоритмов выделения трендов. Формализация задач синтеза алгоритмов выделения трендов. Разрешимость и регулярность. Проблемы локальности. | ||
== Литература == | == Литература == | ||
| + | # {{П:Рудаков 1992 Алгебраическая теория}} | ||
# Букур И., Деляну А. Введение в теорию категорий и функторов. М.: Мир. 1972. | # Букур И., Деляну А. Введение в теорию категорий и функторов. М.: Мир. 1972. | ||
# Журавлев Ю.И. Об алгебраическом подходе к решению задач распознавания или классификации // Проблемы кибернетики. Вып. 33. М.: Наука. 1978. С. 5-69. | # Журавлев Ю.И. Об алгебраическом подходе к решению задач распознавания или классификации // Проблемы кибернетики. Вып. 33. М.: Наука. 1978. С. 5-69. | ||
Текущая версия
|
МАТЕМАТИЧЕСКИЕ МЕТОДЫ КЛАССИФИКАЦИИ (часть 1)
- Обязательный курс для студентов 4 курса каф. ММП, читается в 7 семестре
- Лекции – 36 часов
- Форма контроля - экзамен
- Автор программы: д.ф.-м.н. Рудаков К.В.
- Лектор: д.ф.-м.н. Рудаков К.В.
Аннотация
Основу данного курса составляют теория категорий и теория универсальных и локальных ограничений для задач классификации и распознавания. В курс входит построение теории категорий, изучение понятий категорий, подкатегорий, морфизфов (мономорфизм, эпиморфизм, биморфизм). Рассмотрена задача синтеза алгоритмов, изучены понятия допустимых и корректных алгоритмов, понятие разрешимости. Так же введены понятия полноты семейства алгоритмов и категорий, базы категорий. Изучен критерий регулярности задач классификации. Рассмотрены понятия функциональной сигнатуры и универсальных ограничений.
Содержание курса
Категории
Определение понятия категории. Двойственность. Подкатегории. Традиционное определение полной подкатегории.
Морфизмы
Мономорфизмы. Теорема о композиции мономорфизмов. Мономорфизмы в категории отображений. Эпиморфизмы. Теорема о композиции эпиморфизмов. Эпиморфизмы в категории отображений. Изоморфизмы и биморфизмы. Пример неэквивалентности.
Элементы теории множеств
Декартово произведение произвольной индексированной системы множеств. Аксиома выбора. Парадокс Рассела. Отношение эквивалентности множеств и теорема Кантора-Бернштейна. Парадокс Кантора. Разложение произвольного отображения в суперпозицию отображений определенного вида. Булевы функции. Неявные булевы функции.
Алгебраический подход
Общий вид алгоритмов, синтезируемых методами алгебраического подхода. Лемма о достаточности условий допустимости. Регулярность задач распознавания. Обоснование необходимости условия полноты. Определения баз категорий. Лемма об эквивалентности определений баз для полных допустимых категорий.
Базы
Общая схема перехода от пространства матриц информации к пространству информационных матриц. Лемма о необходимости для, вообще говоря, неодноэлементных баз. Лемма о достаточности для одноэлементных баз.
Г-Полнота
Общий критерий регулярности. Условие 1-Г-полноты. Условие слабой 1-Г-пол-ноты. Корректность. Условие Г-полноты. Условие слабой Г-полноты. Теорема о полноте алгебраических расширений.
Симметрические универсальные ограничения
Определение. Лемма о достаточности использования подгрупп. Лемма о допустимости симметрических категорий. Лемма о полноте симметрических категорий. Лемма о базах.
Функциональные сигнатуры и универсальные ограничения
Категории Ф0, Фi, Фj. Допустимые функциональные сигнатуры. Лемма об условиях существования единичного морфизма. Лемма об условиях существования единичного морфизма. Лемма об условиях замкнутости относительно суперпозиций. Лемма об условиях замкнутости относительно суперпозиций.
Функциональные категории
Лемма о полноте функциональных категорий. Лемма о допустимости функциональных категорий. Лемма о базах.
Литература
- Рудаков, К. В. Алгебраическая теория универсальных и локальных ограничений для алгоритмов распознавания: Дис. док. физ.-мат. наук: 05-13-17. — Вычислительный центр АН СССР, 1992. — 274 с. (подробнее)
- Букур И., Деляну А. Ведение в теорию категорий и функторов. М.: Мир. 1972.
- Журавлев Ю.И. Избранные научные труды. М.: Магистр. 1999.
- Журавлев Ю.И., Исаев И.В. Построение алгоритмов распознавания, корректных для данной выборки // ЖВМ и МФ. 1979. Том 19. № 3. С. 728 738.
- Журавлев Ю.И., Рудаков К.В. Об алгебраической коррекции процедур обработки (преобразования) информации // Прикладная математика и информатика. М.: Наука. 1987. С. 240-251.
- Ленг С. Алгебра. М.: Мир. 1968.
- Мальцев А.И. Алгебраические системы. М.: Наука. 1970.
- Матросов В.Л. Корректные алгебры ограниченной емкости над множествами некорректных алгоритмов // ДАН СССР. 1980. Т. 253. № 1. С. 25-30.
- Рудаков К.В. Универсальные и локальные ограничения в проблеме коррекции эвристических алгоритмов классификации // Кибернетика. 1987. № 2. С. 30-34.
- Рудаков К.В. Полнота и универсальные ограничения в проблеме коррекции эвристических алгоритмов классификации // Кибернетика. 1987. № 3. С. 106-109.
- Рудаков К.В. Симметрические и функциональные ограничения в проблеме коррекции эвристических алгоритмов классификации // Кибернетика. 1987. № 4. С. 35-40.
- Рудаков К.В. О применимости универсальных ограничений при исследовании алгоритмов классификации // Кибернетика. 1987. № 5. С. 32-38.
- Рудаков К.В. Об алгебраической теории универсальных и локальных ограничений для задач классификации // Распознавание, классификация, прогноз. Математические методы и их применение. Вып. 1. М.: Наука. 1989. С. 176-200.
- Фейс С. Алгебра: кольца, модули и категории: В 2-х т. М.: Мир. 1979.
МАТЕМАТИЧЕСКИЕ МЕТОДЫ КЛАССИФИКАЦИИ (часть 2)
- Обязательный курс для студентов 4 курса каф. ММП, читается в 8 семестре
- Лекции – 32 часа
- Форма контроля - экзамен
- Автор программы: д.ф.-м.н. Рудаков К.В.
- Лектор: д.ф.-м.н. Рудаков К.В.
Аннотация
Данный курс составляет часть алгебраического подхода к проблеме синтеза алгоритмов распознавания. В курс входит построение теории категорий, изучение свойств функциональных и симметрических категорий, баз и полноты категорий, соотношений категорий (функциональные подкатегории симметрических категорий и симметрические подкатегории функциональных категорий). Так же в данном курсе изложены основные принципы построения R и Г моделей, классы решаемых задач, их регулярность, полнота и семейства подмоделей. Рассмотрены семейства корректирующих операций, изучены понятия полноты и суперполноты моделей.
Содержание курса
Модель )
Иерархия подмоделей модели . Теорема о полноте модели
. Теорема о полноте модели
. Теорема о неполноте моделей
и
.
Модель )
Иерархия подмоделей модели . Теорема о полноте модели
. Теорема о неполноте моделей
и
.
Одноэлементная база категории 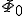
Лемма о существовании одноэлементной базы категории в линейной оболочке базы.
Полнота семейств
Теорема о полноте семейства . Теорема о полноте семейства
. Теорема о 0-1 полноте модели
. Теорема о 0-1 полноте семейства
. Теорема о 0-1 полноте семейства
.
Категории 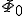 и
и 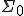
Критерий разрешимости для категорий и
. Теорема о суперполноте для категории
. Теорема о суперполноте для категории
.
Замыкания модели )
Прямая теорема о полноте линейного замыкания модели . Прямая теорема о полноте полиномиального замыкания модели
.
Глобальный и локальный базисы для задач распознавания
Общий итерационный процесс построения локальных базисов задач распознавания. Построение локального базиса в комитете большинства. Построение локального базиса в комитете старшинства. Построение локального базиса в алгоритме бустинга AdaBoost.
Монотонные корректирующие операции
Дефект алгоритмического оператора. Дефект набора алгоритмических операторов. Построение локального базиса для случая монотонных корректирующих операций. Теорема о сходимости итерационного процесса построения проблемно-ориентированного базиса за конечное число шагов в случае монотонных корректирующих операций.
Проблемно-ориентированные теории
Задачи синтеза алгоритмов выделения трендов. Формализация задач синтеза алгоритмов выделения трендов. Разрешимость и регулярность. Проблемы локальности.
Литература
- Рудаков, К. В. Алгебраическая теория универсальных и локальных ограничений для алгоритмов распознавания: Дис. док. физ.-мат. наук: 05-13-17. — Вычислительный центр АН СССР, 1992. — 274 с. (подробнее)
- Букур И., Деляну А. Введение в теорию категорий и функторов. М.: Мир. 1972.
- Журавлев Ю.И. Об алгебраическом подходе к решению задач распознавания или классификации // Проблемы кибернетики. Вып. 33. М.: Наука. 1978. С. 5-69.
- Ленг С. Алгебра. М.: Мир. 1968.
- Мальцев А.И. Алгебраические системы. М.: Наука.1970.
- Рудаков К.В. Об алгебраической теории универсальных и локальных ограничений для задач классификации // Распознавание, классификация, прогноз. Математические методы и их применение. Вып. 1. М.: Наука. 1989. С. 176-200.
- Фейс С. Алгебра: кольца, модули и категории: В 2-х т. М.: Мир. 1979.
- Рудаков К.В., Воронцов К.В. О методах оптимизации и монотонной коррекции в алгебраическом подходе к проблеме распознавания // Доклады РАН. 1999. Т. 367. № 3. С. 314-317.

