Непараметрическая регрессия
Материал из MachineLearning.
Непараметрическая регрессия, в отличие от параметрических подходов, использует модель, которая не описывается конечным числом параметров.
Содержание |
Введение
- Цель регрессионного анализа состоит в осуществлении разумной аппроксимации неизвестной функции отклика
по известным точкам
. В случае малых ошибок наблюдения становится возможным сконцентрировать внимание на важных деталях средней зависимости
от
при ее интерпретации.
Отличие от параметрических подходов
- Процедура аппроксимации обычно называется сглаживанием. По существу эта аппроксимация функции отклика
может быть выполнена двумя способами. Довольно часто используется параметрический подход, заключающийся в предположении, что функция отклика
имеет некоторую предписанную функциональную форму, например, это прямая линия с неизвестными свободным членом и наклоном. Альтернативой этому может служить попытка оценить
непараметрическим образом, без указания конкретного ее вида. Первый подход к анализу регрессионной зависимости называется параметрическим, поскольку предполагается, что вид функции полностью описывается конечным набором параметров. Типичный пример параметрической модели представляет собой полиномиальное уравнение регрессии, когда параметрами являются коэффициенты при неизвестных. Однако при параметрическом подходе молчаливо предполагается, что кривая может быть представлена в терминах параметрической модели, или, по крайней мере, имеется уверенность в том, что ошибка аппроксимации для наилучшего параметрического приближения пренебрежимо мала. Наоборот, в непараметрической модели регрессионной зависимости не производится проектирования данных в "прокрустово ложе" фиксированной параметризации. Предварительное задание параметрической модели может оказаться слишком ограничительным или чересчур малой размерности для аппроксимации непредвиденных характеристик, в то время как непараметрическое сглаживание предоставляет гибкие средства анализа неизвестных регрессионных зависимостей.
- Непараметрический подход приводит, таким образом, к гибкому функциональному виду кривой регрессии.
Разновидности
Ядерное сглаживание
- Одним из простейших методов является ядерное сглаживание. Этот метод прост в применении, не требует дополнительных математических сведений и понятен на интуитивном уровне. Ядерное сглаживание во многих случаях является подходящим средством. Существуют разнообразные альтернативные методы сглаживания такие, например, как сплайны, но в [Хардле В, гл3] показывается, что в асимптотическом смысле они эквивалентны ядерному сглаживанию.
- Ключом к проведению качественного непараметрического оценивания является выбор подходящей ширины окна для имеющейся задачи. Хотя ядерная функция
остается важной, ее главная роль состоит в обеспечении дифференцируемости и гладкости получающейся оценки. Ширина окна
, с другой стороны, определяет поведение оценки в конечных выборках, что ядерная функция сделать просто не в состоянии. Существуют четыре общих подхода к выбору ширины окна:
- референтные эвристические правила
- методы подстановки
- методы кросс-валидации
- бутстраповские методы.
Ради аккуратности подчеркнем, что диктуемые данными методы выбора ширины окна не всегда гарантируют хороший результат.
- Исходя из минимизации глобальной ошибки следует
брать равным::
, где
- неизвестная аппроксимируемая зависимость.
Референтные эвристические правила
- Референтные эвристические правила выбора ширины окна используют стандартное семейство распределений для определения
.
Рассмотрим оценку Парзена-Розенблата для одномерной функции плотности
-
.
-
- В случае семейства нормальных распределений и гауссовского ядра
. На практике применяется
, выборочное стандартное отклонение.
Методы подстановки
Методы подстановки, такие как в Sheather, Jones (1991), состоят в подстановке оценок неизвестной константы в формулу для оптимальной ширины окна на основе первоначальной оценки
, которая в свою очередь основана на «предварительной» ширине окна, например, найденной по правилу
. Все прочие константы в выражении для
известны после выбора ядерной функции
(то есть
и
известны). Хотя такие правила популярны, заинтересованный читатель может обратиться к работе Loader (1999), где обсуждаются относительные достоинства методов подстановки по сравнению с другими методами выбора ширины окна, обсуждаемыми ниже.
Методы кросс-валидации
- Методы кросс-валидация на основе наименьших квадратов – это полностью автоматический и диктуемый данными метод выбора сглаживающего параметра. Этот метод основан на принципе выбора ширины окна, минимизирующей интегральную среднеквадратическую ошибку получающейся оценки. Интеграл квадрата разности
и
имеет вид
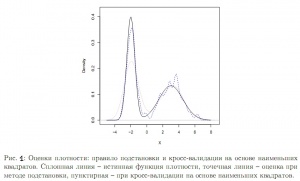
- Можно заменить эти величины их выборочными аналогами, сделать поправку на смещение и получить целевую функцию, которую затем можно минимизировать с помощью численных методов. Этот подход был предложен в работах Rudemo (1982) и Bowman (1984). Для понимания сущности комментариев в Loader (1999) на Рис. 1 изображены оценки бимодальной плотности – ядерная оценка при применении правила подстановки и кросс-валидации на основе наименьших квадратов. Рис. 1 показывает, что на самом деле правило подстановки чрезмерно сглаживает, приводя к существенному смещению в левой вершине. Кросс-валидация на основе наименьших квадратов исправляет это, как отмечает Loader (1999), но ценой дополнительной вариации в правой вершине.
- Одна из проблем данного подхода – его чувствительность к наличию округленных или дискретизированных данных, а также к мелкомасштабным эффектам в данных.
- Из примера следует, что, возможно, ядерную оценку с фиксированным параметром
можно улучшить, и существуют «адаптивные» ядерные оценки, которые позволяют
меняться в точке
или
; см. Abramson (1982) и Breiman, Meisel, Purcell (1977). Эти оценки, однако, способствуют введению ложного шума в оценку плотности. Однако метод с фиксированным
доминирует в прикладных исследованиях.
Бутстраповские методы
- Faraway, Jhun (1990) предложили метод выбора ширины окна
на основе бутстрапа путем оценивания интегральной среднеквадратичной ошибки для каждой фиксированной ширины окна, и затем минимизации по всем значениям. Данный подход использует сглаженный бутстраповский метод на основе начальной оценки плотности. Один из недостатков этого подхода в том, что целевая функция является случайной, что может привести к проблемам при численной минимизации, а также его вычислительная сложность.
Ядерные веса определяют некоторую окрестность вокруг точки лежащей на сетке. Следующий вопрос сглаживания – полиномиальное приближение функции
в этой окрестности.
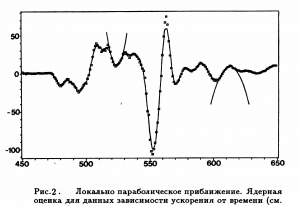
Локально полиномиальное приближение
- Простейшим полиномом приближения в такой окрестности является константа. Ядерная оценка минимизирует сумму квадратов невязок в окрестности точки
, форма и размер которой определяется ядром
.
- Локально полиномиальное приближение и его связь с ядерным сглаживанием подробно исследованы в работе (Muller 1987), где показана их эквивалентность.
- Подробнее также см. Алгоритм LOWESS
kNN оценки
- Конструкция оценок ближайших соседей отличается от ядерных оценок. Ядерная оценка определяется как взвешенное среднее перемененных отклика в фиксированной окрестности точки
, причем веса определялись ядром
и шириной окна
. Оценка k-ближайших соседей представляет собой среднее, взвешенное в изменяющейся окрестности. Эта окрестность определяется только теми значениями переменной
, которые являются
ближайшими к
по евклидову (обычно) расстоянию. Последовательность
весов была введена в работе Loftsgaarden, Quesenberry (1965) для близкой задачи оценивания плотности и использовалась в Cover, Hart(1967) для целей классификации.
- Параметр сглаживания
определяет степень гладкости оценки кривой. Он играет ту же роль, что и ширина окна для ядерных сглаживателей. Влияние переменного
на качественные характеристики оценки аналогочино случаю ядерных оценок с прямоугольным ядром.
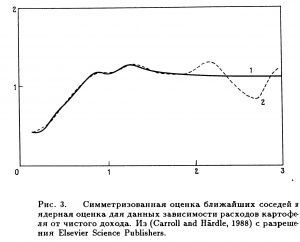
- На Рис. 3. изображен пример сравнения ядерного сглаживания с квартическим ядром и
сглаживания. Ширина окна выбиралась методом кросс-проверки. Данные прогонялись через окна шириной
для ядерного сглаживания на отрезке
и
для оси значений. Получившиеся кривые регрессии практически совпадают для
, где лежит большая часть данных. При бо‘льших значения
наблюдается существенное расхождение кривых: ядерная оценка показывает очевидное бимодальное соотношение, а симметризованная оценка ближайших соседей указывает либо на асимптоту, либо даже на слабое убывание с ростом дохода. В контексте задачи, кажется, что последнее содержит больше смысла с точки зрения экономики...
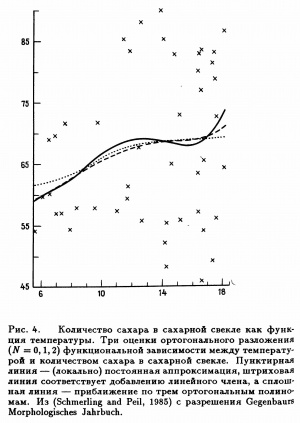
Оценки ортогональных разложений
Предположим, что функция регрессии может быть представлена в виде ряда Фурье
,
- где
- известна система базисных функций, а
- неизвестные коэффициенты Фурье. В работе Szego (1959) приведены условия, при которых такое представление возможно. Хорошо известными системами базисных функций являются полиномы Лагерра и полиномы Лежандра. Как только фиксирован базис функций, проблема оценивания функции регрессии может быть сведена к оцениванию коэффициентов Фурье. Конечно, существует определенная трудность, состоящая в том, что может быть бесконечно много ненулевых коэффициентов
. Таким образом, при заданном конечном объеме выборки
можно эффективно оценить лишь подмножество коэффициентов.
- Пример применения показан на Рис. 4.
Сглаживание сплайнами
Общей мерой близости к данным для некоторой кривой является сумма квадратов невязок
- Если
может любой кривой - неограниченной в функциональном смысле - то эта мера, имеющая смысл расстояния, равна нулю для всякой кривой
, интерполирующей данные. Подход, основанный на сглаживании сплайнами, исключает эту нежелательную интерполяцию данных за счет достижения компромисса между двумя противоречивыми целями: получить хорошую аппроксимацию данных и получить кривую, не имеющую слишком быстрых локальных изменений.
- Известны различные способы количественной оценки локальных изменений. Можно определить меру плавности кривой, основанную, например, на первой, второй, и более старших производных. Для успешного раскрытия основной идеи удобнее всего ввести интеграл от квадрата второй производной, т.е. для количественной оценки локального изменения использовать штраф за нарушение плавности
.
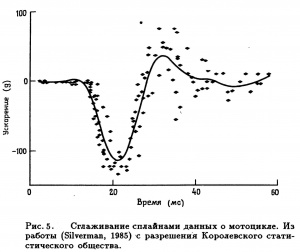
- Пример сглаживания сплайнами представлен на Рис. 5. интерпретация данных: данные о мотоцикле [ Значения
(в мс) после смоделированного столкновения с мотоциклом. Переменная отклика
- ускорение (в g) посмертного тестирования объекта. Из Schmidt, Mattern, Schiiler (1981)]
Перечень менее распространенных методов
Рекуррентные методы
- Предположим, что данные
наблюдаются не как выборка фиксированного объема
, а как последовательность пар
поступающих с выхода некоторого устройства наблюдения. Такие устройства присутствуют в задачах контроля (surveillance problems), управления (control operations) или вмешательства(intervention problems). В общем случае можно рассматривать данные как временной ряд. Поскольку непараметрическая
оценка обычно определяется по всей выборке, ее приходится пересчитывать при поступлении новых данных. Следовательно, с вычислительной точки зрения предпочтительнее, чтобы оценка регрессии, основанная на точках, строилась исходя из
-го наблюдения
и оценки, полученной по первым
точкам, без вызова предыдущих данных из памяти компьютера.
Регрессограмма
- Этот термин был введен Тьюки (Tukey, 1961) для того, чтобы подчеркнуть связь этой оценки с гистограммой. Регрессограмма представляет собой среднее тех значений переменных отклика, для которых соответствующие величины
попадают в один из интервалов разбиения пространства наблюдений переменной
Tukey(1947) - ее можно рассматривать как аппроксимацию
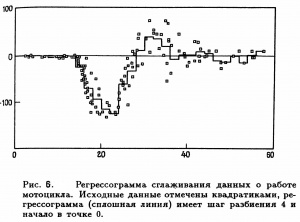
ступенчатой функцией, и она фактически является ядерной оценкой (с прямоугольным ядром), вычисленной в средних точках интервалов разбиения. На Рис. 6. изображены данные о работе мотоцикла и регрессограмма при шаге разбиения 4.
Медианное сглаживание
- Предположим, что целью аппроксимации является кривая условий медианы
, а не кривая условного среднего. Последовательность "локальных медиан" для значений переменной отклика определяет медианный сглаживателъ. Медианное сглаживание сыграло важную роль в историческом развитии методов сглаживания.
- Эта оценка имеет очевидную аналогию с
-оценкой, но отличается, по крайней мере, в двух аспектах: медианное сглаживание устойчиво по отношению к большим выбросам, и с помощью этого метода появляется возможность моделировать разрывы кривой регрессии
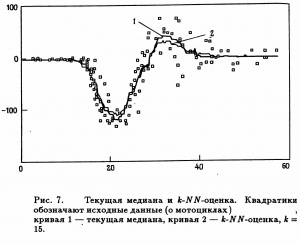
. На Рис. 7. на примере данных о мотоциклах(cм. пояснение к рисунку 5) приведено сравнение двух методов оценивания — медианного сглаживания и
-оценки.
- Этот пример выявляет свойство робастности медианного сглаживания. Медианная оценка не подвержена влиянию группы возможных выбросов в районе точки
, и она несколько ближе к основной массе данных в двух «областях всплесков»
. Некоторый недостаток состоит в том, что по своей природе оценка медианного сглаживания является грубой характеристикой.
Литература
- Хардле В. Прикладная непараметрическая регрессия. — 1989.
- Расин, Джеффри «Непараметрическая эконометрика: вводный курс». — Квантиль, №4, стр. 7–56., 2008.
Ссылки
- Abramson, I.S. On bandwidth variation in kernel estimates – a square root law. Annals of Statistics 10. — 1982. — С. 1217–1223.
- Bowman, A.W. An alternative method of cross-validation for the smoothing of density estimates. Biometrika 71. — 1984. — С. 353–360.
- Breiman, L., W. Meisel, E. Purcell Variable kernel estimates of multivariate densities. Technometrics 19. — 1977. — С. 135–144.
- Cover, T. M. and Hart, P. E. Nearest neighbor pattern classification. IEEE Transactions on Information Theory, 13. — 1967. — С. 21-27.
- Faraway, J., M. Jhun Bootstrap choice of bandwidth for density estimation. Journal of the American Statistical Association 85. — 1990. — С. 1119–1122.
- Loader, C.R. Bandwidth selection: Classical or plug-in? Annals of Statistics 27. — 1999. — С. 415–438.
- Loftsgaarden, D. O., Quesenberry, G. P. A nonparametric estimate of a multivariate density function. Annals of Mathematical Statistics, 36. — 1965. — С. 1049-1051.
- Muller H. G. Weighted local regression and kernel methods for nonparametric curve fitting. Journal of the American Statistical Association, 82. — 1987. — С. 231-238.
- Rudemo, M. Empirical choice of histograms and kernel density estimators. Scandinavian Journal of Statistics 9. — 1982. — С. 65–78.
- Schmidt, G. Mattern, R., Schiiler, F. Biomechanical investigation to determine physical and traumatological differentiation criteria for the maximum load capacity of head and vertebral column with and without protective helmet under effects of impact. EEC Research Program on Biomechanics of Impacts. Final Report Phase III, Project 65, Institut fur Rechtsmedizin, Universitat Heidelberg, West Germany.. — 1981. — С. 231-238.
- Sheather, S., M. Jones A reliable data-based bandwidth selection method for kernel density estimation. Journal of Royal Statistical Society, Series B 53. — 1991. — С. 683–690.
- Szego, G. Orthogonal polynomials. Amer. Math. Soc. Coll. PubL, 23. — 1959.
- Tukey, J. W. Nonparametric estimation II. Statistically equivalent blocks and tolerance regions. The continuous case. Annals of Mathematical Statistics, 18. — 1947. — С. 529-539.
См. также
— Валентин Голодов 18:37, 8 января 2010 (MSK)