Центральное множество
Материал из MachineLearning.
(→Определение) |
|||
| Строка 7: | Строка 7: | ||
Максимальный шар множества <tex>\Omega</tex> также называется '''максимальным пустым шаром''' или '''максимальным вписанным шаром'''. | Максимальный шар множества <tex>\Omega</tex> также называется '''максимальным пустым шаром''' или '''максимальным вписанным шаром'''. | ||
| - | '''Центральным множеством''' ('''central set''') или '''[[Скелет|скелетом]''' ('''skeleton''') <tex>\Omega</tex> называется множество <tex>S_{\Omega}</tex> центров пустых шаров <tex>\Omega</tex>. | + | '''Центральным множеством''' ('''central set''') или '''[[Скелет|скелетом]]''' ('''skeleton''') <tex>\Omega</tex> называется множество <tex>S_{\Omega}</tex> центров пустых шаров <tex>\Omega</tex>. |
== Пример == | == Пример == | ||
Версия 21:48, 27 февраля 2011
Центральное множество является математической формализацией понятия скелета объекта для пространств произвольной размерности.
Содержание |
Определение
Пусть --- связное открытое ограниченное подмножество
.
Замкнутая шаровая окрестность точки
называется максимальным шаром множества
, если для любой точки
и любой ее замкнутой шаровой окрестности
из того, что
следует, что
.
Максимальный шар множества также называется максимальным пустым шаром или максимальным вписанным шаром.
Центральным множеством (central set) или скелетом (skeleton) называется множество
центров пустых шаров
.
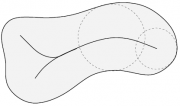
Пример
При центральное множество ([[Скелет|скелет]) представляет собой множество центров максимальных пустых кругов плоской фигуры.
Связь между медиальным и центральным множествами
Для любого связного открытого ограниченного множества верно, что его медиальное множество
является подмножеством его центрального множества:
.
При ,
, если
--- многоугольная фигура.